"多元函数图像制作与插值方法"

本次实验五主要目的是了解二元函数图形的制作，掌握空间曲面等高线的制作方法，了解多元函数插值方法，并学习掌握MATLAB软件相关命令。在实验中，我们通过使用MATLAB中的mesh和surf命令来绘制二元函数图形。其中，mesh(x,y,z)命令用于画网格曲面，将数据点在空间中描绘出来并连成网格，而surf(x,y,z)命令则用于画出完整的曲面。在准备阶段，我们需要了解mesh和surf命令的基本用法，并通过练习程序来熟悉这些命令的操作。 在实验中，我们以z = x + y为例来绘制函数的图形。首先，我们定义横坐标x和纵坐标y的取值范围，然后使用meshgrid函数生成对应的数据点坐标矩阵X和Y。接着，我们将得到的数据点坐标矩阵X、Y和函数值矩阵z传入mesh命令，绘制出函数的网格曲面。之后，我们再次传入相同的数据点坐标矩阵X、Y和函数值矩阵z到surf命令中，得到完整的曲面图形。通过这些步骤，我们可以清晰地展示出二元函数z = x + y的图形特征。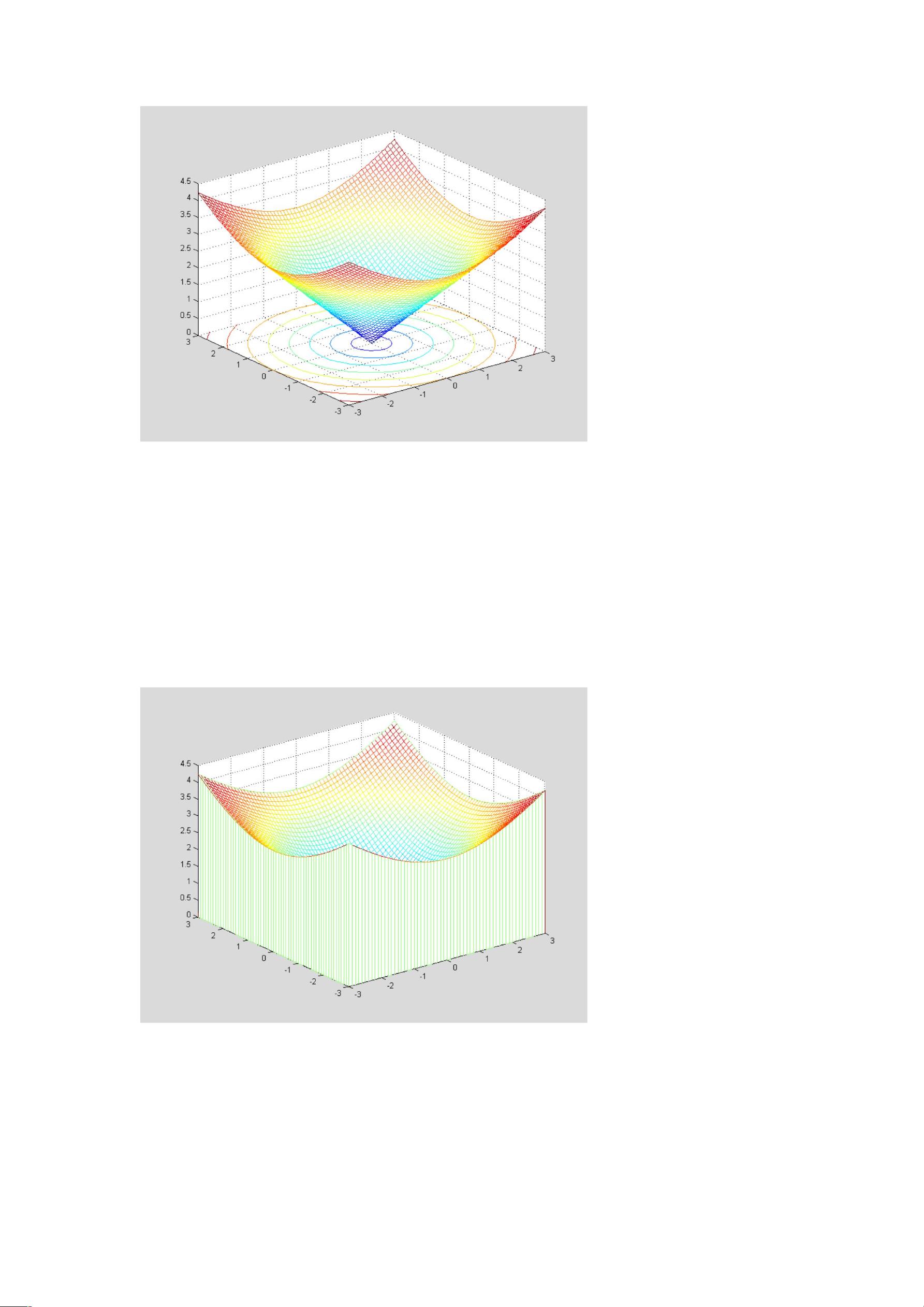 除了绘制函数的图形，我们还可以利用等高线的绘制方法来描绘函数在三维空间中的等高线。通过画出不同高度处的曲线，我们可以更直观地了解函数的变化趋势和曲面的特点。在MATLAB中，我们可以使用contour和contourf命令来绘制空间曲面的等高线。通过定义等高线的数值范围和密度等参数，我们可以得到清晰的等高线图形。这种方法不仅可以更全面地展示出函数的空间特性，还可以为我们提供更多关于函数行为的信息。 总的来说，通过本次实验，我们不仅学会了如何绘制二元函数的图形和等高线，也加深了对多元函数插值方法的理解，进一步熟悉了MATLAB软件相关命令的应用。这些知识和技能的掌握不仅对于进一步学习数学建模和数据分析有帮助，也为我们日后在实际工作中处理复杂数据和函数提供了重要的基础。通过实践和练习，我们能够更熟练地运用这些方法，并将其应用到更广泛的领域中去，为我们未来的学习和工作打下坚实的基础。