MATLAB多项式操作与曲线拟合教程

"该资源是一份关于MATLAB的教程，主要来自清华大学，涵盖了多项式、曲线拟合、插值、三次样条、数值分析以及符号数学工具等多个主题。教程详细讲解了MATLAB的使用，包括如何安装和进行基础操作，如绘制图形和处理多项式。在多项式部分，介绍了如何找根、乘法、加法、除法、求导、估值等。在数值分析中涉及了绘图和极小化问题。此外，教程还深入到符号数学，包括符号表达式的运算、微分积分、简化格式化以及方程求解和线性代数内容。" MATLAB作为一款强大的数学和工程计算软件，被广泛应用于各个科学领域。本教程首先从基础的MATLAB安装和使用入手，通过实例展示了如何绘制简单的函数图形，如使用`t=-20:0.01:20`定义时间轴，`yt=pi*abs(sin(t/2))`计算函数值，然后用`plot(t,yt)`绘制图形，加上`grid on`指令以显示网格。 在多项式章节中，教程详细阐述了MATLAB处理多项式的方法。MATLAB使用行向量表示多项式，系数按降序排列。例如，多项式x^4 - 12x^3 + 0x^2 + 25x + 116可以表示为`p=[1 -12 0 25 116]`。函数`roots(p)`用于找出多项式的根，而`poly(r)`则可以将根转换回对应的多项式形式。值得注意的是，MATLAB会默认包含零系数项，并且在处理复数根时可能存在截断误差。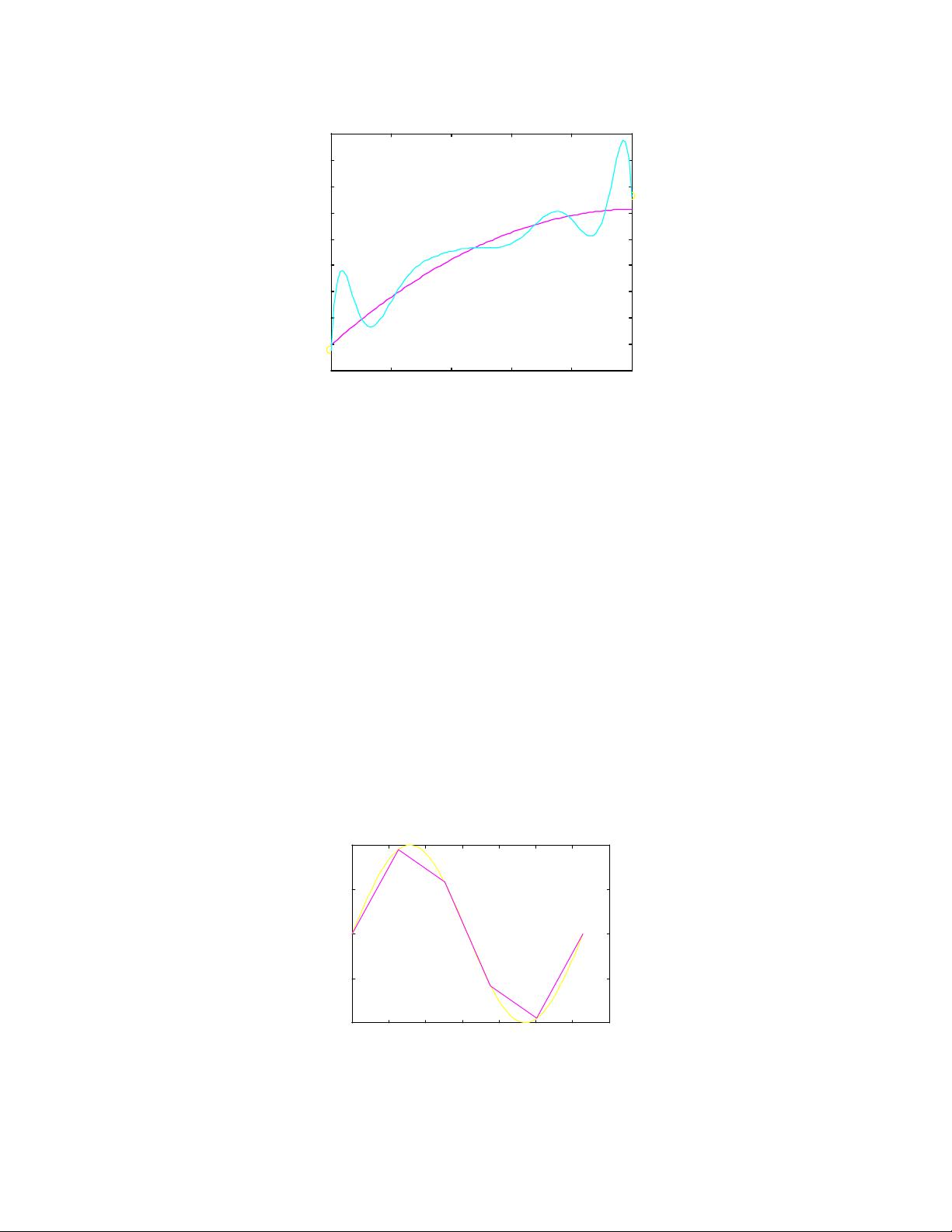 在曲线拟合和插值部分，教程涵盖了从一维到二维的插值方法，这对于数据处理和模型建立非常重要。三次样条章节讨论了其基本特征、分段多项式、积分和微分等概念，这些在数值分析中经常使用。 数值分析章节则涉及了图形绘制和极小化问题，MATLAB提供了强大的绘图功能，可以方便地展示复杂的数据和结果。同时，它也能用于寻找函数的局部极小值，这在优化问题中尤为关键。 最后，教程还介绍了MATLAB的符号数学工具箱，允许用户进行符号运算，如创建和操作符号表达式，进行微分和积分，求解方程，以及进行高精度计算。这对于理论研究和解析解的求解非常有用。 这份MATLAB教程由浅入深，覆盖了MATLAB的基本功能和高级应用，对于初学者和进阶用户来说都是宝贵的学习资源。通过学习，读者可以掌握MATLAB的多项式操作、数值计算、图形绘制以及符号运算，提升科研和工程计算能力。