MEMS陀螺仪随机误差补偿技术与Kalman滤波应用

"该资源是一篇关于MEMS(微电子机械系统)陀螺仪随机误差补偿方法的研究论文，发表于2009年。论文主要针对MEMS陀螺仪的随机漂移误差，提出并比较了两种基于Kalman滤波理论的补偿方法。通过建立陀螺仪随机误差模型，详细推导了滤波方程，并通过实验验证了这两种方法的有效性，特别是后一种方法在滤波和跟踪性能上的优势。" 文章中涉及的知识点包括： 1. **MEMS陀螺仪**：MEMS陀螺仪是一种微型传感器，用于测量物体的角速度，广泛应用于惯性导航、无人机控制、智能手机等设备中。由于制造工艺和物理效应，它们可能存在随机漂移误差，影响测量精度。 2. **随机漂移误差**：这是MEMS陀螺仪常见的性能问题，表现为输出信号随着时间的推移出现非线性漂移，降低了传感器的长期稳定性。 3. **Kalman滤波理论**：一种用于估计动态系统状态的最优滤波算法，通过融合来自多个传感器的数据，可以有效地减少噪声和误差，提高数据准确性。 4. **等随机和等随机加速假设**：论文依据陀螺仪输出角速率信息的变化特点，提出了两种假设作为误差建模的基础，分别对应不同的滤波策略。 5. **误差模型**：建立陀螺仪随机误差模型是进行误差补偿的关键步骤，模型能描述误差随时间的变化规律。 6. **Kalman滤波方程**：在误差模型基础上，推导出适应MEMS陀螺仪随机误差的Kalman滤波方程，用于计算最优的误差补偿值。 7. **实验验证**：通过实际微惯性测量系统中的MEMS陀螺仪输出信号分析，验证了两种补偿方法的正确性和有效性，证明后一种方法在滤波和跟踪性能上更优。 8. **信号完整性和耦合噪声**：虽然这部分内容似乎与MEMS陀螺仪的主题不直接相关，但提到了信号完整性和耦合噪声的问题，这通常是在高速数字电路和微波系统设计中考虑的重要因素，与微带线和PCB参数密切相关。 9. **时域有限差分法（FDTD）**：一种计算电磁场的数值分析方法，适用于分析微带线、微带非连续性等复杂电磁问题，文中提及FDTD在研究微带线信号完整性和耦合噪声方面的作用。 10. **吸收边界条件**：在FDTD模拟中，通过使用完全匹配层（Perfectly Matched Layer, PML）来模拟理想的吸收边界，以减少反射并提高仿真精度。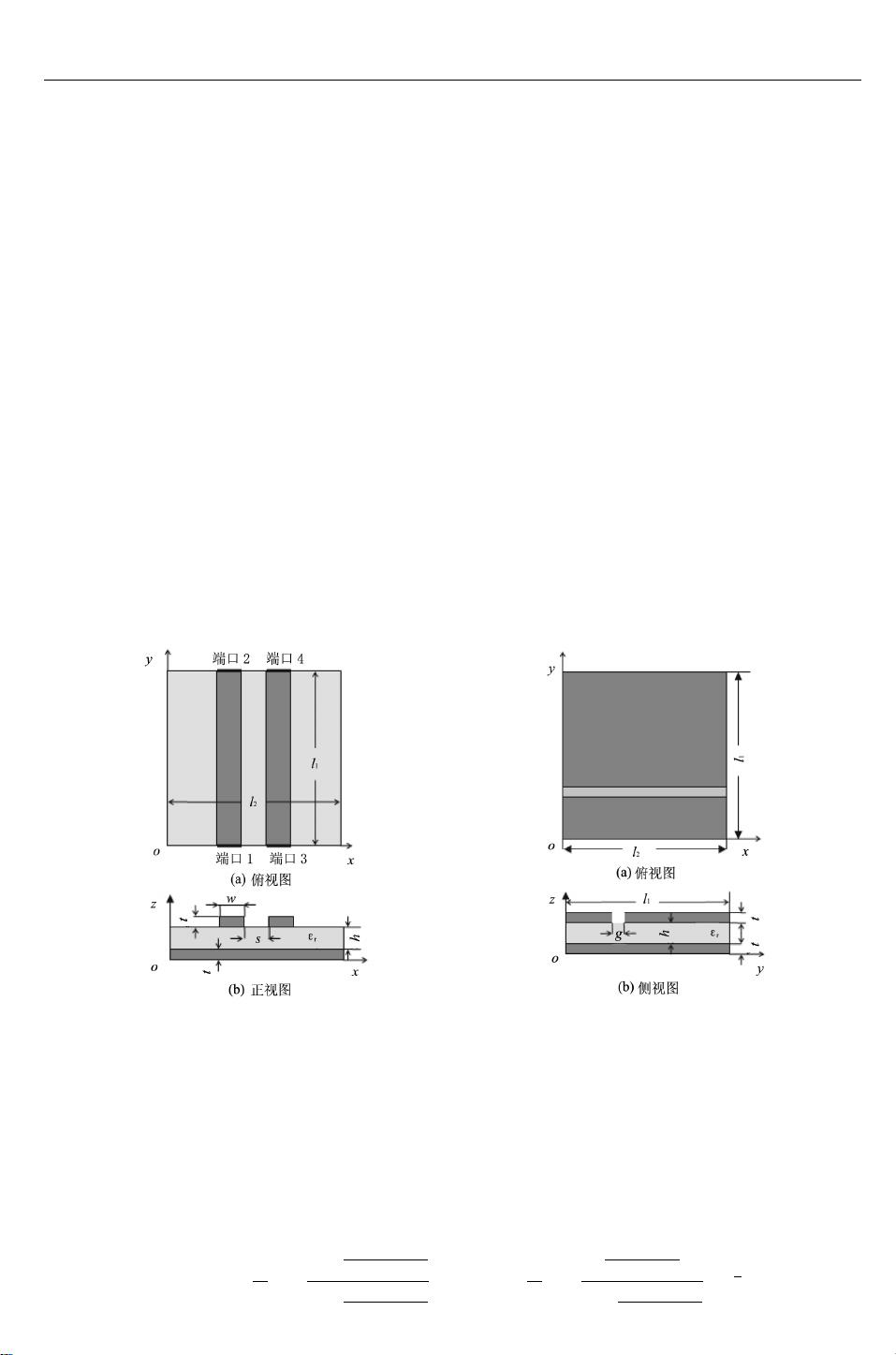 11. **电路参数**：如微带线的长度、宽度、厚度、内部边缘距离，以及返回路径的长度、宽度、厚度和介质基板的参数，这些都影响微带线的电气特性。 这篇论文不仅探讨了MEMS陀螺仪的误差补偿技术，还涉及到信号完整性和电磁场分析的相关知识，展示了多学科交叉在解决实际工程问题中的应用。