Matlab实现采样定理：信号恢复与频谱分析

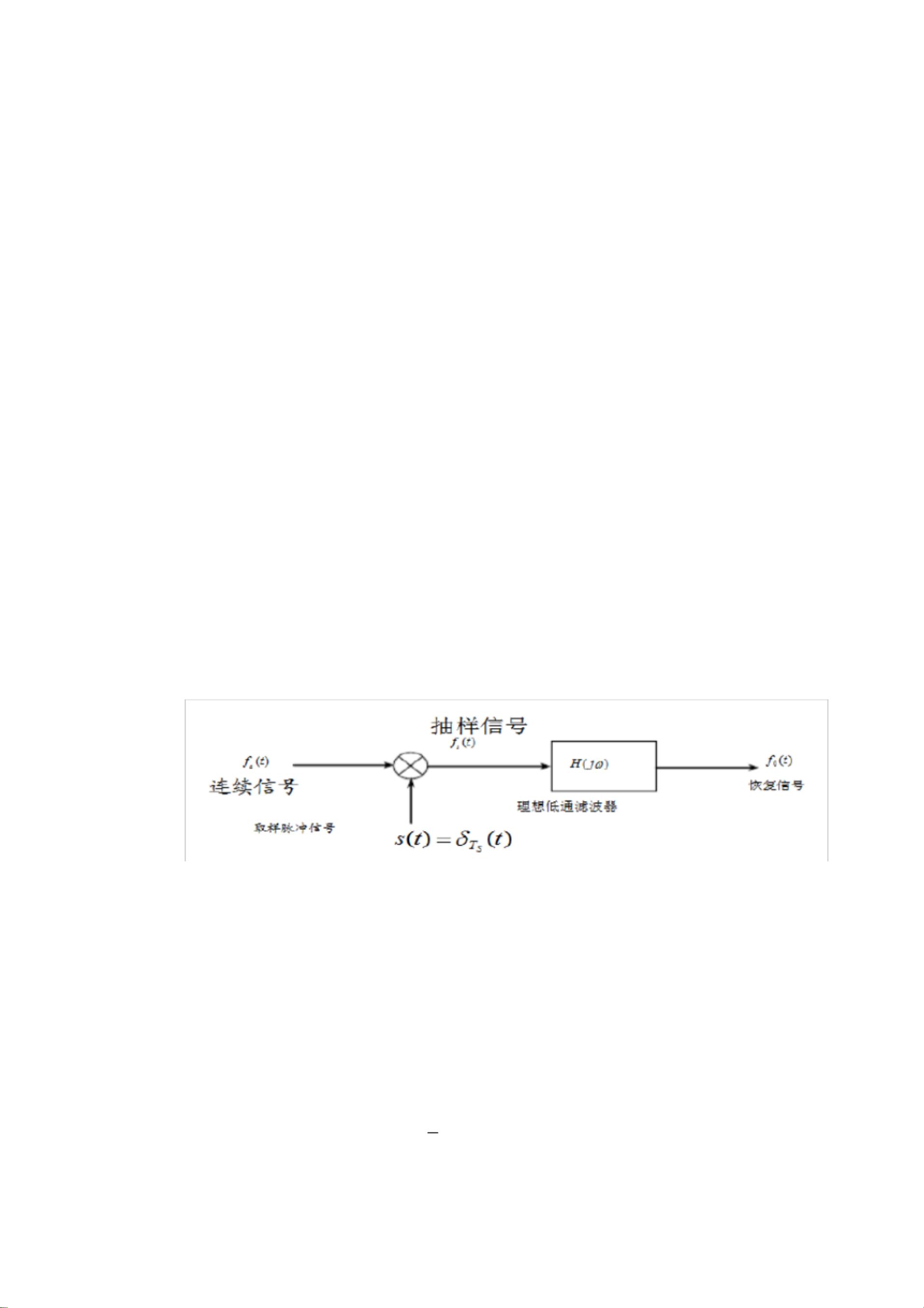
"基于matlab的采样定理验证" 采样定理是数字信号处理中的一个核心概念，它阐述了如何从连续时间信号中获取离散时间样本，并且能够无失真地恢复原始信号。本实验的目标是通过MATLAB来理解和验证这一理论。 在实验环境中，你需要使用MATLAB这一强大的数学计算和仿真软件。MATLAB提供的强大信号处理工具箱，使得我们可以方便地创建、分析和可视化各种信号，包括进行采样和信号恢复的操作。 采样定理的要点在于，如果一个连续信号的最大频率成分是f_c，那么为了不失真地恢复该信号，采样频率fs应当至少是2f_c，这个条件通常被称为奈奎斯特定理。采样过程可以表示为信号与一个周期性脉冲序列的卷积，而这个序列的周期就是采样间隔。在频域中，采样信号的频谱是原信号频谱的周期性复制。 在MATLAB中，可以通过编程模拟采样过程。首先，创建一个代表连续时间信号的函数，例如正弦波或复指数函数。然后，使用离散采样间隔对这个函数进行采样，生成离散的采样序列。你可以使用`fft`函数来查看采样信号的频谱，观察是否出现了频谱混叠现象。 信号恢复是采样定理的逆过程，它涉及到从采样序列中重构原始连续信号。这通常通过低通滤波器实现，该滤波器能有效地去除高于f_c的高频成分，只保留那些可以通过采样得到的信息。MATLAB的滤波器设计工具可以帮助设计这样的滤波器，并应用到采样序列上，以恢复信号。 预习内容应涵盖采样定理的基本概念，理解什么是奈奎斯特频率，以及为什么采样频率需要大于2倍的信号最高频率。同时，熟悉MATLAB的基本操作，如创建信号、采样和滤波器设计也是必要的。 实验内容可能包括以下几个部分： 1. 创建一个具有已知最高频率的连续时间信号，如正弦波。 2. 使用MATLAB进行等间隔采样，观察采样后的序列。 3. 分析采样信号的频谱，判断是否存在频率混叠。 4. 设计并应用一个低通滤波器，通过滤波器对采样序列进行处理。 5. 比较滤波后的序列与原始信号，验证是否能成功恢复原始信号。 通过这个实验，你不仅能深入理解采样定理的原理，还能掌握在实际应用中如何利用MATLAB进行信号处理。实验过程中的每一步都提供了对理论的直观验证，从而加强了理论知识的理解。