数据概括性度量：集中趋势、离散程度与偏态分析

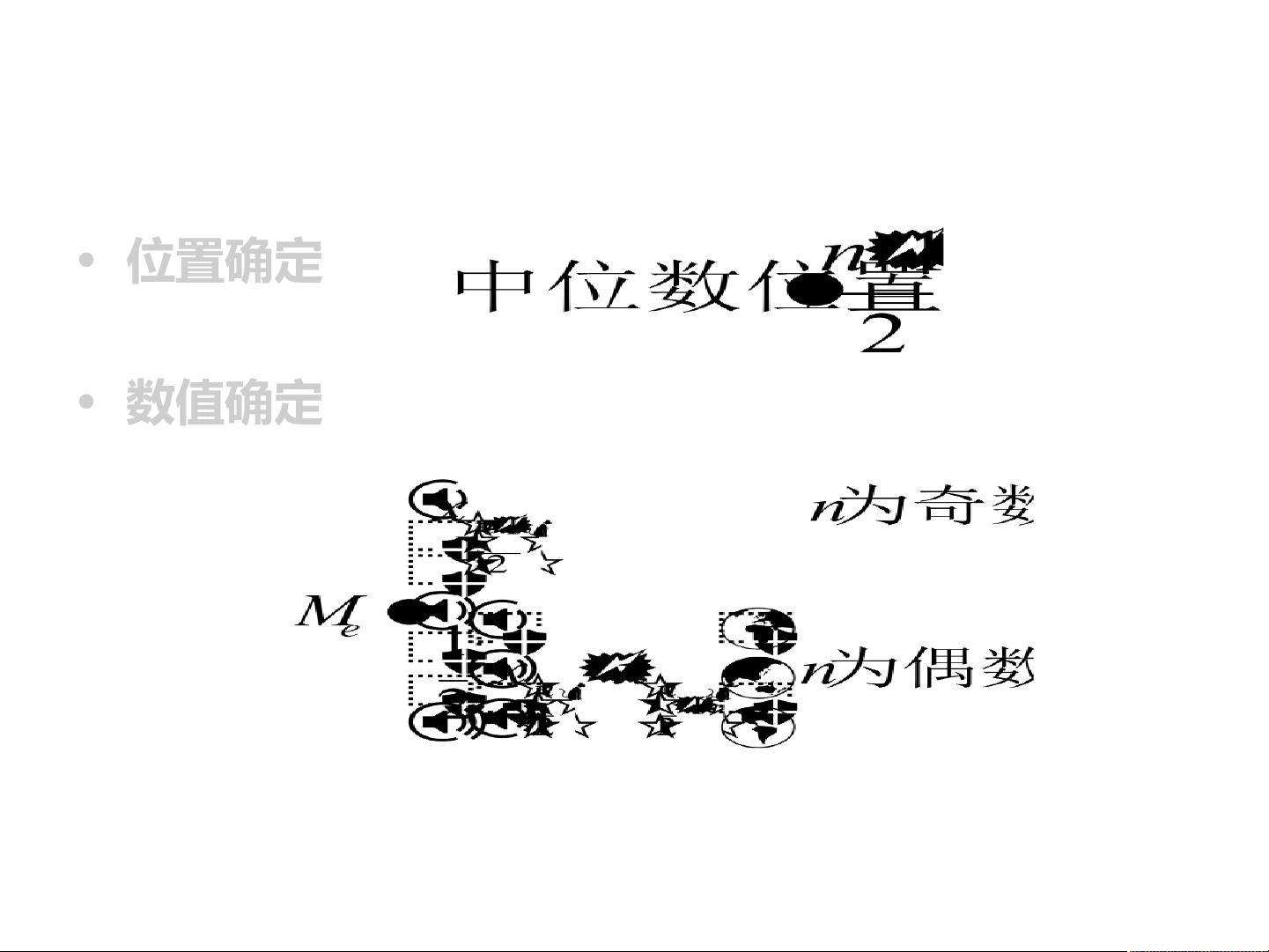
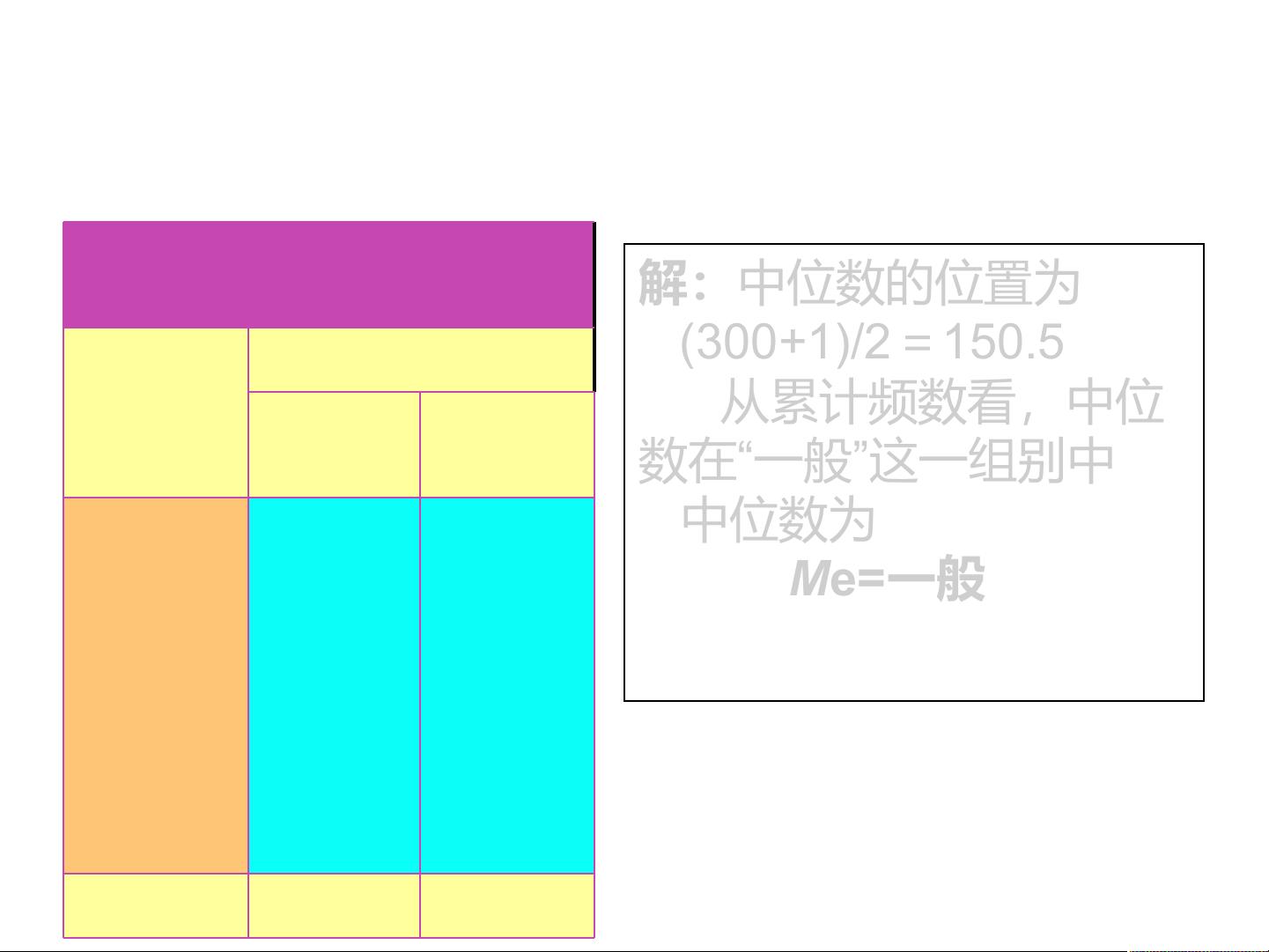
"第三章---数据的概括性度量PPT课件.ppt" 本章主要探讨了数据的概括性度量，这是统计学中衡量数据集特性的重要方法。集中趋势、离散程度以及偏态与峰态是数据分布特征的三大核心概念。 集中趋势描述了一组数据的中心位置，反映了数据向中心值靠拢的程度。它帮助我们理解数据的典型值或最常见的数值。针对不同类型的数据，有相应的集中趋势度量方法： 1. 分类数据：众数（Mode）是出现频率最高的数据值。众数不受极端值的影响，尤其适用于数据量较大且分布不均匀的情况。一个数据集可能有一个众数，也可能没有，甚至有多个众数。 2. 顺序数据：中位数（Median）是将数据按顺序排列后位于中间位置的值。它同样对极端值不敏感，特别适用于数据分布呈偏斜的情况。 3. 数值型数据：平均数（Mean）是最常见的集中趋势度量，即所有数据值的和除以数据的数量。平均数能够受极端值影响，因此在数据分布不均匀时可能不是一个很好的代表值。 3.1.1 众数（Mode）的概念包括： - 它是一组数据中出现次数最多的数值。 - 在处理大量数据时，计算众数较为实用。 - 众数对极端值不敏感，因此较为稳定。 - 数据集可能没有众数（例如，每个数值出现次数相同），或存在一个以上的众数。 - 众数不仅适用于分类数据，也适用于顺序数据和数值型数据，但通常对分类数据更有意义。 例如，在一项关于消费者饮料偏好的调查中，如果调查了50人，其中15人选择“可口可乐”，则“可口可乐”成为众数，因为它是最受欢迎的品牌，占比30%。 离散程度的度量则关注数据的分散程度，例如方差、标准差、四分位距等，这些指标帮助我们了解数据的变异性和稳定性。偏态和峰态则是衡量数据分布形状的特征，偏态描述数据分布的对称性，而峰态则表示数据分布的尖峭程度或扁平程度。 通过综合分析集中趋势、离散程度和分布形态，我们可以全面地了解数据集的特性和行为，从而在数据分析、决策制定和研究中提供有价值的见解。在实际应用中，选择合适的度量方式对于准确解读数据至关重要。