K-NN-Centroid: 新一代密度启发式聚类算法

40 浏览量更新于2024-08-26 收藏 467KB PDF 举报

"一种新的基于k-NN中心密度启发式密度的聚类算法，由Xiaochun Wang、Yiqin Chen和Xia Li Wang等人提出，旨在解决DBSCAN等传统密度聚类算法中参数选择的困难问题。该算法结合了k-NN和中心密度的概念，提高了参数选择的合理性和聚类效果的准确性。实验结果在多个数据集上验证了新算法的有效性。" 基于密度的聚类算法是数据挖掘中的一种关键技术，尤其适用于发现具有不规则形状和不同密度的聚类。传统的密度聚类算法，如DBSCAN (Density-Based Spatial Clustering of Applications with Noise)，由于其对邻域半径(ε)和最小点数(minPts)的敏感性，往往在实际应用中面临参数设定的挑战。不恰当的参数选择可能导致聚类结果的质量下降，甚至无法正确识别某些聚类。本研究提出的新型算法——k-NN-Centroid-Inspired Density-Based Clustering Algorithm（k-NN-CDBSCAN），借鉴了k-NN（k最近邻）的思想和中心密度的概念，旨在降低参数选择的难度，同时保持聚类的准确性。k-NN方法通过寻找一个对象的最近邻来评估其环境，而中心密度则考虑了对象与其邻居的距离以及邻居的密度，这种结合使得聚类更具鲁棒性，对参数变化不那么敏感。在k-NN-CDBSCAN算法中，首先，通过k-NN搜索确定每个点的邻域，并计算其邻域内的点的中心密度。然后，根据中心密度的大小和分布，将点分类为核心点、边界点或噪声点。核心点是高密度区域的代表，边界点位于密度下降的边缘，而噪声点则属于低密度区域。接着，通过连接核心点及其边界点形成聚类，以此构建聚类结构。由于算法对参数的依赖性降低，使得用户更容易选择合适的k值，从而简化了聚类过程。实验部分，作者在多个具有不同特性的数据集上对比了新算法与经典算法如DBSCAN的表现。结果表明，k-NN-CDBSCAN在保持聚类质量的同时，对参数的选择更为宽容，且在复杂数据集上的性能优于DBSCAN。这证实了新算法在处理各种密度聚类问题时的优越性。关键词：密度聚类、中心密度、k-NN、k-NN基心密度聚类，反映了该研究的核心内容和技术点。这篇论文提出的新算法为解决基于密度的聚类算法的参数选择问题提供了一个有前景的解决方案，对于数据挖掘领域的实践者和研究人员具有重要的参考价值。

A New k-NN-Centroid-Inspired Density-Based Clustering Algorithm

Xiaochun Wang, Yiqin Chen

School of Software Engineering

Xi’an Jiaotong Unversity

Xi’an, China

{xiaocchunwang@mail, chenyiqin@stu}.xjtu.edu.cn

Xia Li Wang

School of Information Engineering

Changan University

Xi’an, China

xlwang@chd.edu.cn

Abstract—Density-based clustering algorithms are well known

for identifying clusters possessing very different local densities

and existing in different regions of data space. However, the

parameters required by most popular density-based clustering

algorithms, such as DBSCAN, are hard to determine but have

significant impacts on the clustering results. In this paper, we

present a new density-based clustering algorithm in which the

selection of appropriate parameters is less difficult but more

meaningful. Experiments performed on several datasets show

the effectiveness of our approach.

Keywords-density-based clustering; centroid; k nearest

neighbors; k nearest neighbors-based centroid

I. INTRODUCTION

Being an important branch of data mining techniques,

many clustering algorithms have been introduced in the past

few decades, including partition-based clustering [1,2],

density-based clustering [3,4], grid-based clustering [5,6],

graph-based clustering [7,8] and hierarchical clustering

[9,10]. By taking neighbourhood characteristics into account,

density-based clustering algorithms count to be the most

advanced and robust approach, and embody no principle

with clearly defined algorithmic properties. To find clusters

of different shapes, sizes, and densities, recent efforts focus

on their effectiveness and ability to discover clusters of

increasingly complex shapes [9,10], and the scalability to the

size of large datasets to be clustered [11].

Compared with other clustering algorithms, traditional

density-based clustering algorithms using only global

parameter settings have difficulty revealing the skewed

distribution often associated with modern large

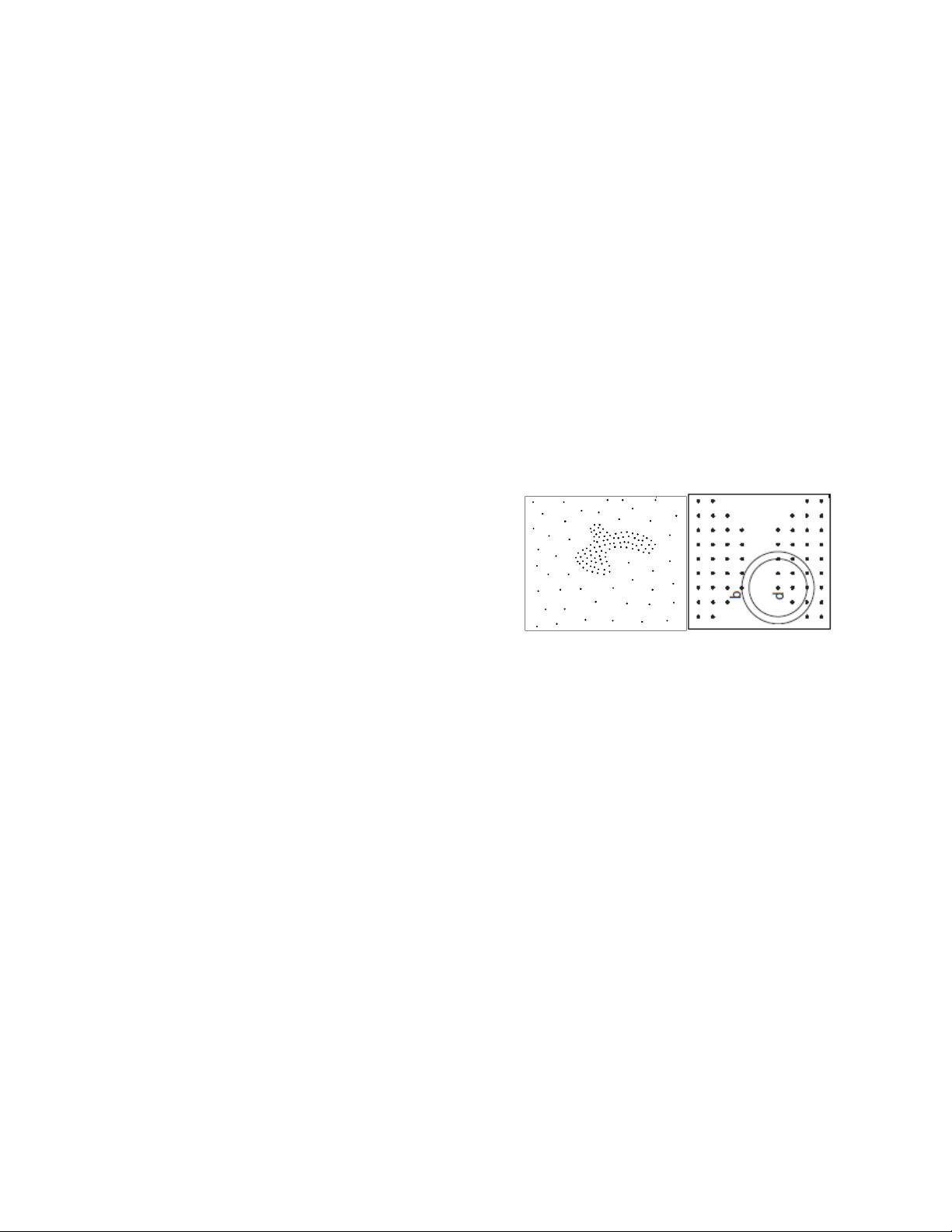
multidimensional real world data sets, as illustrated in the

left plot of Fig.1, which is referred to in this paper as density-

separated clustering problems. In this illustration, there are

two kinds of boundary points, those which reside in the

denser cluster whose k nearest neighbors are all data points

in the same cluster and therefore have similar densities, and

those which reside on the touching side of two clusters of

different densities and, therefore, whose k nearest neighbors

come from different clusters and may have different

densities. Further, the values for input parameters required

by modern density-based clustering algorithms are usually

difficult to determine, and, for slightly different parameter

settings, very different partitions of a data set can be

produced, as manifested in the right plot of Fig.1, which is

referred to in the following as distance separated clustering

problems. In this case, two clusters of similar density exist.

If, for example, k is selected to be no more than 8, two

clusters can be separated easily. However, if k is set to be 16,

k-nearest neighbors based clustering algorithm can not set

these two clusters apart.

Figure 1. (left) density separated clusters, (right) distance separated

clusters

Motivated by these limitations, in this paper, we propose

a new algorithm for local-density based cluster analysis. In

this new algorithm, the concept of centroid based on k-

nearest neighbours of each object in a data set is introduced

whose distance to the data object is used to represents the

degree of how well a data point is surrounded by others, and

is next used to determine a suitable value for k which is

subsequently used to detect clusters in a data set. Another

challenge to meet in this paper is how to define a density

measure for data points residing on the touching side of two

clusters of different densities. For this matter, we propose the

concept of the first neighborhood of a data point.

In the following, we first provide a brief discussion of

some related work on density-based clustering in Section 2.

We then present the concept of k-nearest neighbours based

centroid and the proposed clustering strategy in Section 3. In

Section 4, a performance evaluation of the effectiveness of

the proposed algorithm is conducted. Finally, conclusions are

made in Section 5.

II. R

ELATED WORK

Being a very popular branch in data clustering, density

based clustering algorithms rely on a local density criterion

to form clusters and can detect clusters of different shapes,

sizes, and densities. Early density based clustering

下载后可阅读完整内容，剩余5页未读，立即下载

weixin_38602098

粉丝: 3
资源: 963

K-NN-Centroid: 新一代密度启发式聚类算法

数据挖掘十大经典算法.doc

聚类处理的蚁群算法在旅行商问题中的应用 (2).docx

k-均值算法和k-中心点算法是聚类数据划分算法的典型算法

如何写一个基于K-means算法的红酒聚类

基于K-Means的聚类算法原理

基于k-means聚类算法的图像区域分割技术的行业标准

基于K-Means聚类算法的项目可行性分析

基于K-means算法实现的文本聚类

基于K-mean的深度聚类

比较和分析原型聚类算法和密度聚类算法

最新资源