"分治法解决排序、查找、组合问题及大整数和矩阵乘法"

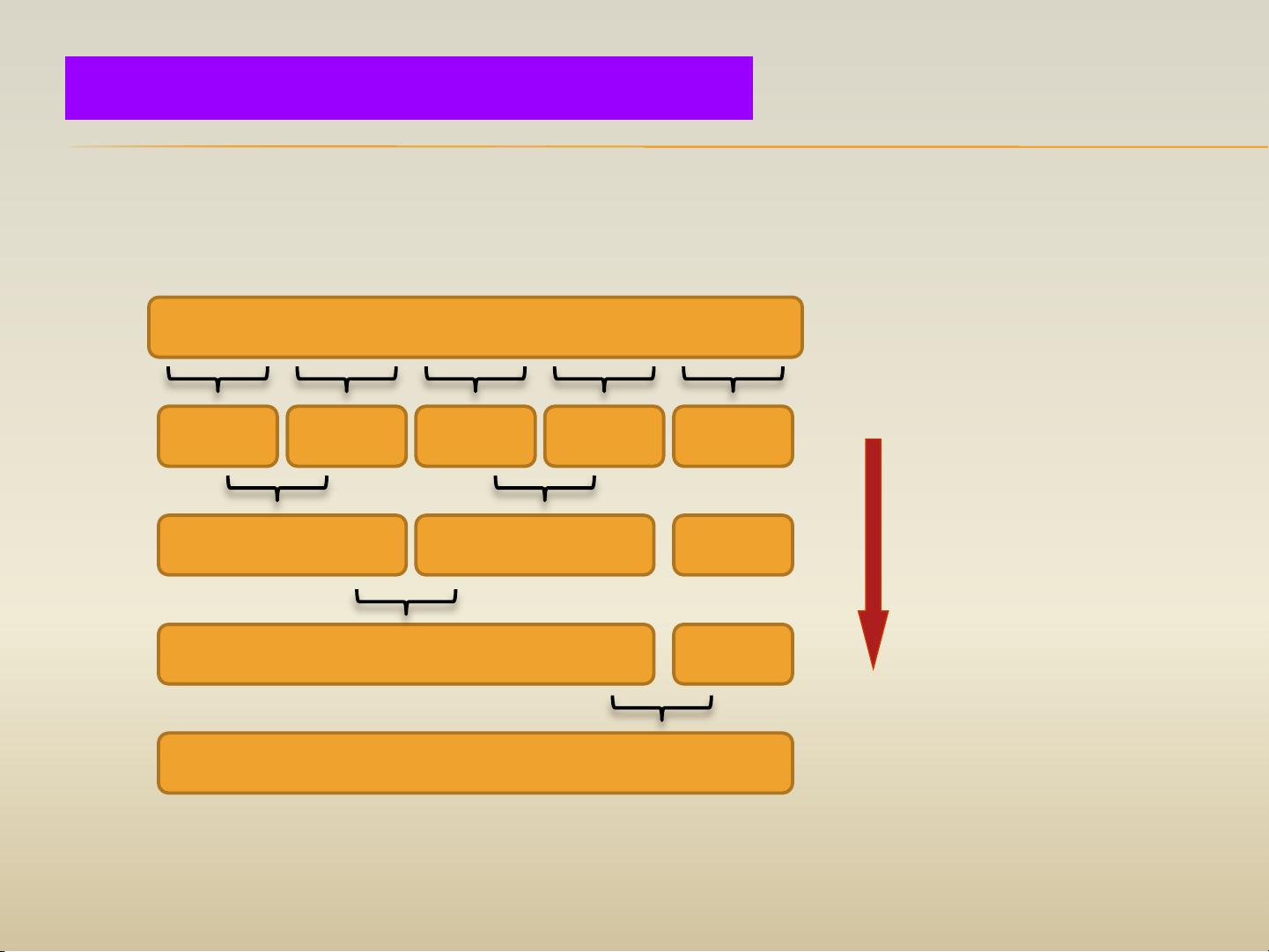
3.1 分治法 分治法是一种算法设计策略，适用于解决规模较大的问题，它的基本思想是将原问题分解为若干个规模较小且相互独立的子问题，递归地解决这些子问题，最后将它们的解合并得到原问题的解。分治法通常采用递归算法设计技术，在每一层递归上都包含三个步骤：分解、求解子问题和合并。分治法能够解决的问题一般具有以下几个特征：问题的规模可以缩小到一定程度就能容易地解决，问题可以分解为若干个规模较小的相同问题，利用子问题的解可以合并为原问题的解，子问题之间相互独立且不包含公共的子问题。 3.2 求解排序问题 在分治法中，解决排序问题是一个常见的应用。排序问题是指将一组数据按照一定的顺序进行排列的问题，常见的排序算法有快速排序、归并排序等。使用分治法解决排序问题通常是将原始的数据集合分解为若干个规模较小的子集合，然后递归地对子集合进行排序，最后将排好序的子集合合并成最终的有序集合。通过这种方式，可以更加高效地解决排序问题，并且得到较好的时间复杂度。 3.3 求解查找问题 除了排序问题，分治法也可以用于解决查找问题。查找问题是在一组数据中寻找特定元素的问题，常见的查找算法有二分查找、线性查找等。分治法可以通过将原始数据集合分解为规模较小的子集合，然后递归地在子集合中进行查找，最终找到目标元素。这种方式可以提高查找的效率，并且降低时间复杂度。 3.4 求解组合问题 另外，分治法还可以应用于解决组合问题。组合问题是指从给定的n个元素中选取m个元素，所有可能的选取情况称为一个组合。通过分治法，可以将组合问题分解为多个规模较小的子问题，然后递归地求解这些子问题，最后合并得到所有可能的组合情况。这种方法可以更加高效地解决组合问题，并且提高算法的性能。 3.5 求解大整数乘法和矩阵乘法问题 此外，分治法还可以用于求解数学计算问题，例如大整数乘法和矩阵乘法问题。这些问题都可以通过将原始问题分解为规模较小的子问题，然后递归地求解这些子问题，并最终将子问题的解合并得到原始问题的解。通过这种方式，可以更加高效地解决大整数乘法和矩阵乘法问题，并且降低时间复杂度。 3.6 并行计算简介 最后，分治法还可以与并行计算结合，提高算法的效率。并行计算是指将多个计算任务同时进行，以提高整体计算的效率。在分治法中，可以将问题分解为多个子问题，并且利用并行计算的方式同时解决这些子问题，最后将子问题的解合并得到原始问题的解。通过这种方式，可以加快算法的执行速度，并且提高算法的并行性。 综上所述，分治法是一种十分有效的算法设计策略，可以应用于解决多种类型的问题，包括排序问题、查找问题、组合问题、大整数乘法和矩阵乘法问题等。通过分解原始问题为规模较小的子问题，递归地求解这些子问题，并最终将子问题的解合并得到原始问题的解，可以更加高效地解决大规模的复杂问题。并且结合并行计算，还能进一步提高算法的执行效率，使得分治法在实际应用中具有广泛的应用前景。