改进的可逆数据隐藏技术：PVO与自适应成对嵌入
74 浏览量
更新于2024-08-27
1
收藏 2.69MB PDF 举报
"这篇研究论文探讨了一种改进的可逆数据隐藏方法，该方法结合了像素值排序（PVO）和自适应成对嵌入技术。这种方法主要用于在图像中隐藏数据，同时保持图像的可逆性，即在数据提取后，原始图像能够完全恢复。论文指出，传统的PVO技术虽然有效，但在处理像素预测误差时没有充分利用像素间的相关性，这可能导致隐藏数据的效率不高。"
正文:
可逆数据隐藏（Reversible Data Hiding, RDH）是一种在不影响原始数据完整性的情况下嵌入额外信息的技术。它广泛应用于版权保护、信息隐藏和数据安全等领域。论文"Improved Reversible Data Hiding based on PVO and Adaptive Pairwise Embedding" 提出了一种新的策略来提高RDH的效率和隐藏容量。
首先，像素值排序（Pixel-Value Ordering, PVO）是RDH中的基础步骤。PVO将图像分割成不重叠的等大小块，并对每个块内的像素值进行升序排列。通过选取第二大/小的像素值作为最大/小像素值的预测，可以计算出两个预测误差。这种方法的优点是数据嵌入后，块内的PVO顺序保持不变，确保了可逆性。
然而，论文的关键创新在于其观察到在每个块内，两个预测误差的修改可以独立进行，而无需考虑像素之间的相关性。这一发现意味着可以更有效地利用这些误差空间来嵌入更多的数据。论文提出了一种自适应成对嵌入策略，该策略利用像素间的相关性来优化预测误差的修改，从而提高数据隐藏的效率。
自适应成对嵌入算法可能包括以下步骤：分析像素块内的统计特性，根据这些特性调整预测误差的修正方式；利用相邻像素的相关性来预测和校正误差，减少由于错误修正导致的视觉质量下降；并根据预测误差的分布动态调整数据嵌入的策略，确保数据的稳定性和图像质量。
通过这种改进，不仅可以提高隐藏数据的数量，还能保持图像的质量和可逆性。此外，由于这种方法是自适应的，它能够根据不同的图像内容和需求进行调整，进一步增强了其在实际应用中的灵活性和适用性。
这项研究为RDH提供了一个新的视角，即通过更智能地处理像素预测误差和利用图像内部的结构信息，可以显著提高数据隐藏的性能。这为未来的RDH技术发展开辟了新的可能性，特别是在高容量和高质量图像隐藏的需求日益增长的背景下。
687Journal of Real-Time Image Processing (2019) 16:685–695
1 3
of each block may be modified in the data embedding pro-
cedure, for each
1 ≤ i ≤ n − 1
,
p
𝜎
(i)
can be recovered as
p
𝜎
(i)
itself.
Furthermore, the smallest pixel value
p
𝜎
(1)
in each block
can also be modified (either decreased by 1 or unchanged) to
embed data. The similar data embedding and extraction pro-
cedures are omitted here.
2.2 Improved PVO‑based RDH [35]
In the original PVO-based RDH method, the blocks with
d
max
= 0
are not utilized to carry data. However, these blocks
are usually smooth and suitable for reversible embedding.
Based on this consideration, to take the advantage of the
blocks with
d
max
= 0
, an improved PVO-based method is
proposed by Peng etal. [35].
For the data embedding of this method, first, for a given
block with sorted values
(p
𝜎
(1)
, ..., p
𝜎
(n)
)
, instead of comput-
ing the prediction-error
d
max
in (1) as the original PVO-based
method does, it is redefined as follows considering the order
of
𝜎(n − 1)
and
𝜎(n)
Clearly, one can verify that the redefined prediction
error satisfies
d
max
≥
0
if
𝜎(n) >𝜎(n − 1)
and
d
max
< 0
if
𝜎(n) <𝜎(n − 1)
. That is to say, the prediction error defined
in this way is ranged from
−∞
to
+∞
. For example, for the
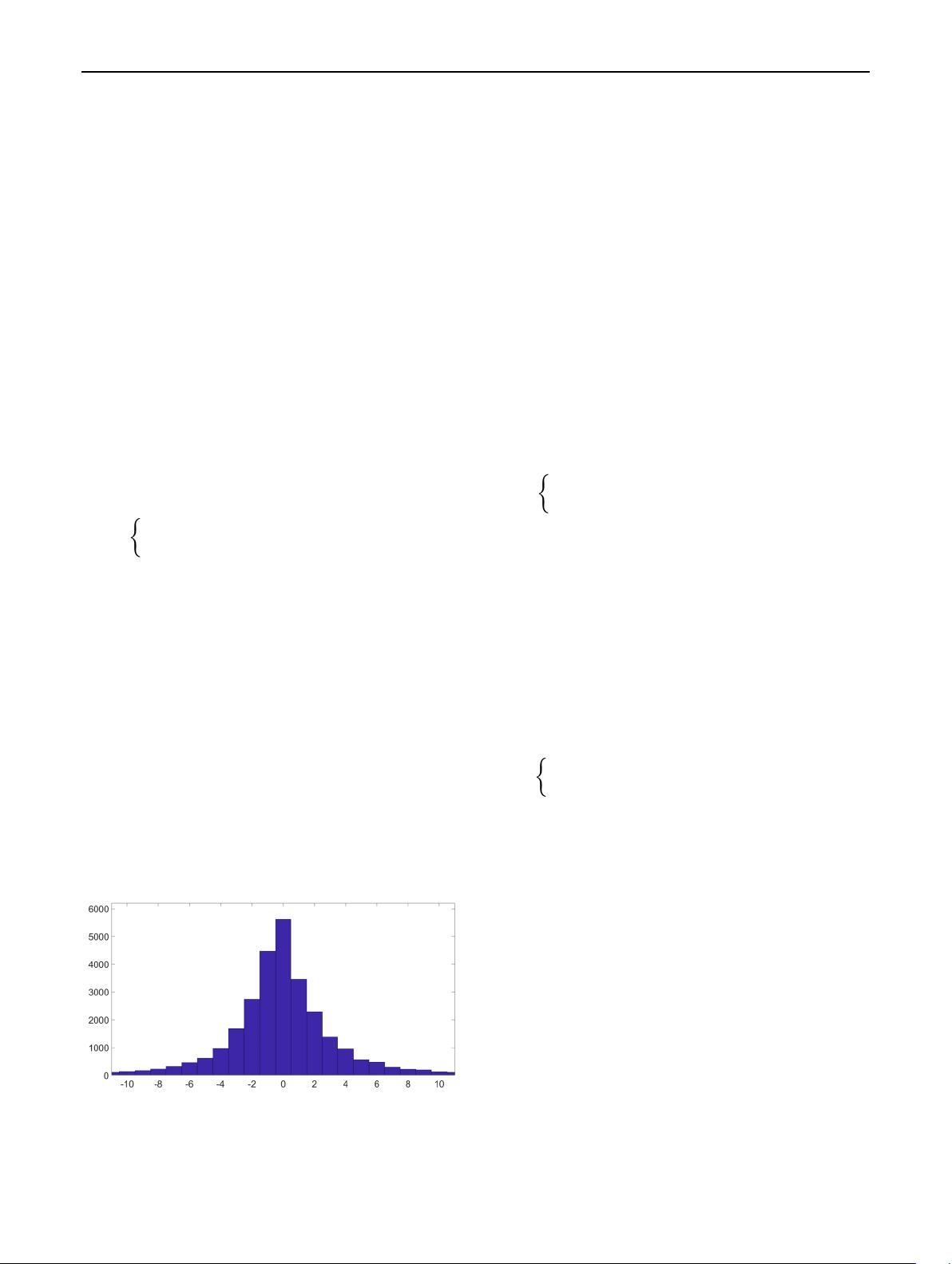
Lena image, the histogram of the redefined prediction error
d
max
is shown in Fig.2. This histogram is a Laplacian-like
distribution centered at 0 with two sides decay. Then, the
bins 0 and
−1
are expanded for data embedding. More spe-
cifically,
d
max
is modified to derive the marked prediction-
error
d
max
in the following way:
(6)
d
max
=
{
p
𝜎(n)
− p
𝜎(n−1)
, if 𝜎(n) >𝜎(n − 1)
p
𝜎
(n−1)
− p
𝜎
(n)
, if 𝜎(n) <𝜎(n − 1)
.
(7)
d
max
=
⎧
⎪
⎨
⎪
⎩
d
max
+ b, if d
max
= 0
d
max
− b, if d
max
=−1
d
max
+ 1, if d
max
≥ 1
d
max
−
1, if d
max
≤ −
2,
where
b ∈{0, 1}
is a to-be-embedded data bit. Accordingly,
the largest pixel value
p
𝜎
(n)
is modified as:
to derive the marked pixel value.
For this improved method, a key issue is that, unlike other
expansion-shifting based RDH methods, the expansion bins
cannot be arbitrarily selected. To guarantee the reversibility,
the sign of each prediction error (i.e., “
≥ 0
” or “
< 0
”) should
not be changed after data embedding.
Similar to [34], in each block, only the largest pixel value
p
𝜎
(n)
is either increased by 1 or unchanged, while other
pixel values remain unchanged. The PVO of each block is
unchanged as well and, thus, the recovery and extraction
process can be conducted accordingly. Specifically, for the
decoder, the marked prediction-error
d
max
is first computed
for a marked block with sorted values
(
p
𝜎
(1)
, ...,
p
𝜎
(n)
)
as
follows:
Then, recover the original pixel value
p
𝜎
(n)
as:
In addition, for each
1 ≤ i ≤ n − 1
,
p
𝜎
(i)
is recovered as
p
𝜎
(i)
itself. And, the embedded data bit is 0 if
d
max
∈{0, −1
}
or
1 if
d
max
∈{
1,
−
2}
.
Besides, in this method, the smallest pixel value
p
𝜎
(1)
of
each block is also modified for data embedding, by consider-
ing the prediction error defined as:
One can verify that
d
min
≥
0
if
𝜎(2) >𝜎(1)
, and
d
min
< 0
if
𝜎(2) <𝜎(1)
. The histogram of
d
min
is also a Laplacian-like
distribution centered at 0 with two sides decay. For brevity,
the similar data embedding and extraction procedures by
modifying the smallest pixel value are omitted here and the
details can be found in [35].
2.3 Pairwise PEE [18]
To better utilize the image redundant and improve the
conventional PEE-based reversible embedding, the so-
called pairwise PEE is proposed in [18] by modifying the
2D prediction-error histogram for data embedding. In this
method, the prediction errors are jointed into pairs to gener-
ate a 2D prediction-error histogram and, based on a specifi-
cally designed 2D mapping, it aims to reduce the embedding
(8)
p
𝜎
(n)
= p
𝜎
(n−1)
+
|
d
max
|,
(9)
�
d
max
=
{
�p
𝜎(n)
− �p
𝜎(n−1)
, if 𝜎(n) >𝜎(n − 1)
�p
𝜎
(n−1)
− �p
𝜎
(n)
, if 𝜎(n) <𝜎(n − 1)
.
(10)
p
𝜎(n)
=
{
p
𝜎(n)
, if
d
max
∈{0, −1}
p
𝜎
(n)
− 1, otherwise
.
(11)
d
min
=
{
p
𝜎(2)
− p
𝜎(1)
, if 𝜎(2) >𝜎(1)
p
𝜎
(1)
− p
𝜎
(2)
, if 𝜎(2) <𝜎(1)
.
Fig. 2 Histogram of
d
max
defined in (6), for the standard
512 × 512
sized gray-scale image Lena with block size of
2 × 2
剩余10页未读，继续阅读
2021-04-16 上传
2021-03-15 上传
2021-03-31 上传
2007-03-11 上传
2011-11-18 上传
2006-04-26 上传
2019-09-11 上传
2022-05-16 上传
2021-09-07 上传
weixin_38544152
- 粉丝: 4
- 资源: 923
我的内容管理
展开
最新资源
- Android圆角进度条控件的设计与应用
- mui框架实现带侧边栏的响应式布局
- Android仿知乎横线直线进度条实现教程
- SSM选课系统实现：Spring+SpringMVC+MyBatis源码剖析
- 使用JavaScript开发的流星待办事项应用
- Google Code Jam 2015竞赛回顾与Java编程实践
- Angular 2与NW.js集成：通过Webpack和Gulp构建环境详解
- OneDayTripPlanner：数字化城市旅游活动规划助手
- TinySTM 轻量级原子操作库的详细介绍与安装指南
- 模拟PHP序列化:JavaScript实现序列化与反序列化技术
- ***进销存系统全面功能介绍与开发指南
- 掌握Clojure命名空间的正确重新加载技巧
- 免费获取VMD模态分解Matlab源代码与案例数据
- BuglyEasyToUnity最新更新优化：简化Unity开发者接入流程
- Android学生俱乐部项目任务2解析与实践
- 掌握Elixir语言构建高效分布式网络爬虫
