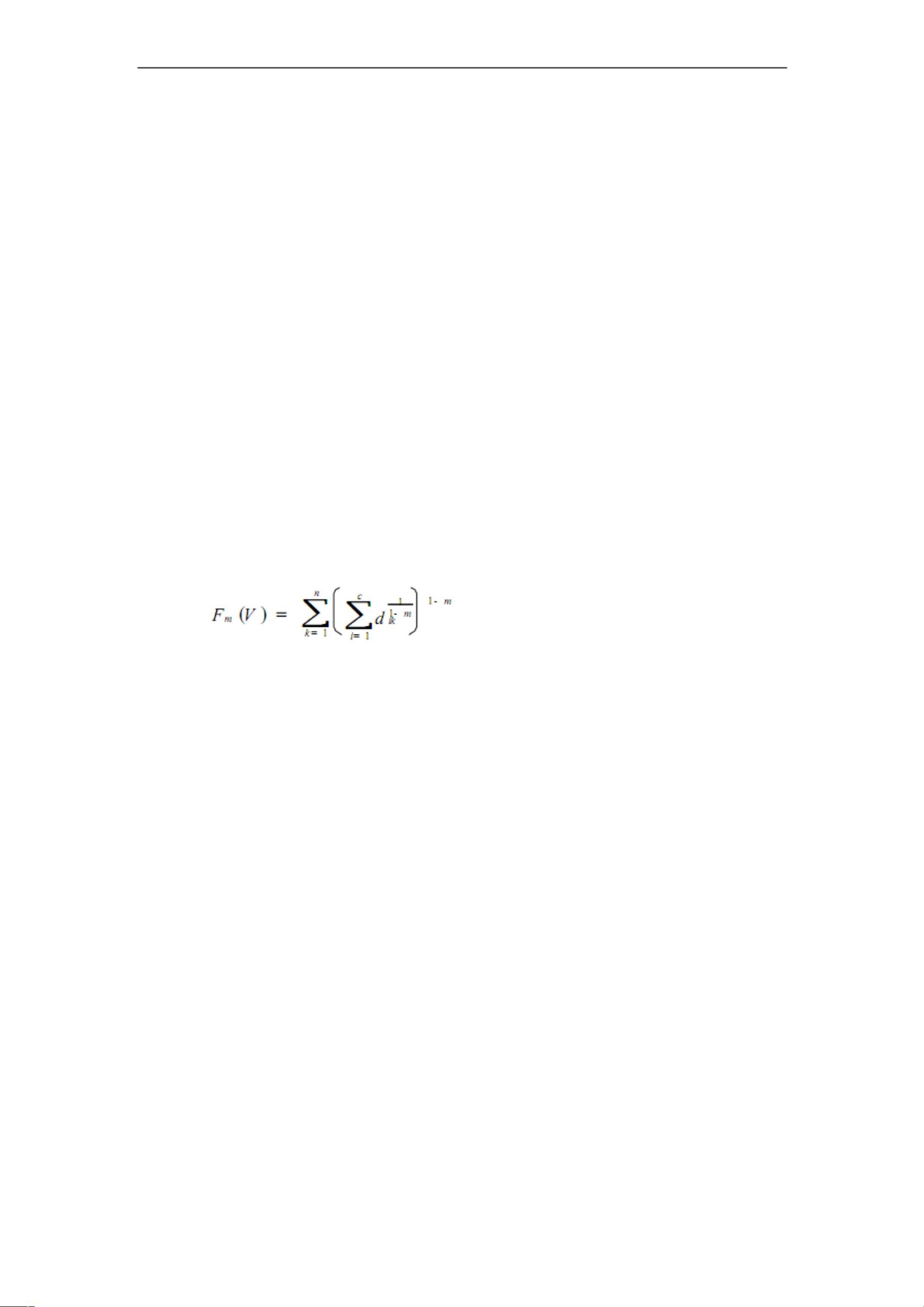模糊C均值聚类算法的实现与应用

"模糊C均值聚类算法的C实现代码" 模糊C均值聚类算法（Fuzzy C-Means, FCM）是聚类分析中的一种，尤其在计算机科学、数据分析和机器学习领域中广泛应用。它属于模糊聚类算法，与传统的K-Means等硬聚类算法不同，模糊C均值算法允许样本点同时隶属于多个类别，这使得它在处理数据不确定性或重叠类别时更为灵活。 模糊C均值算法的核心在于计算样本点对每个类别的隶属度，这通过一个模糊度参数m来控制。隶属度函数μ(x)定义了样本x属于类别Ci的程度，其值介于0和1之间。算法的目标是最小化以下的模糊聚类代价函数： J = ∑(∑(μi(j)^m * (xi - cj)^2))^(1/m) 其中，xi是样本点i的特征向量，cj是类别Ci的中心，μi(j)是样本i属于类别j的隶属度，m是模糊因子，对算法的结果有显著影响。 FCM算法的步骤如下： 1. 初始化：选择C个初始质心（类别中心），通常随机选取数据集中的样本点作为初始聚类中心。 2. 计算隶属度：对于每个样本点，根据其与所有类别中心的距离，利用模糊度参数m计算其对每个类别的隶属度。 3. 更新质心：根据当前的隶属度分布，重新计算每个类别的质心，公式为：cj = ∑(μi(j)^2 * xi) / ∑(μi(j)^2)。 4. 检查停止条件：如果质心的改变量小于预设阈值，或者达到最大迭代次数，算法终止；否则，返回步骤2继续迭代。 在实际应用中，选择合适的C和m至关重要。C代表聚类的数量，通常需要根据问题的具体领域知识或实验结果来设定。m的值越大，样本点所属类别的模糊性就越低，更接近硬聚类；反之，m的值越小，模糊性越高，样本点可能同时属于多个类别。通常，m取值在1.5到2之间可以得到较好的聚类效果。 在编程实现模糊C均值算法时，需要注意优化计算过程，避免不必要的计算和内存消耗，尤其是在处理大数据集时。此外，还可以采用各种策略来改善算法的性能，例如使用并行计算、启发式初始化方法或引入距离度量的调整。 模糊C均值聚类算法是一种强大的工具，用于处理具有模糊边界和不确定性数据的聚类问题。它的灵活性和对数据复杂性的适应性使其在图像分析、数据挖掘、模式识别等多个领域都有重要应用。理解和掌握FCM算法及其C语言实现，对于提升数据分析能力至关重要。