数学建模与Logistic模型在MATLAB中的应用

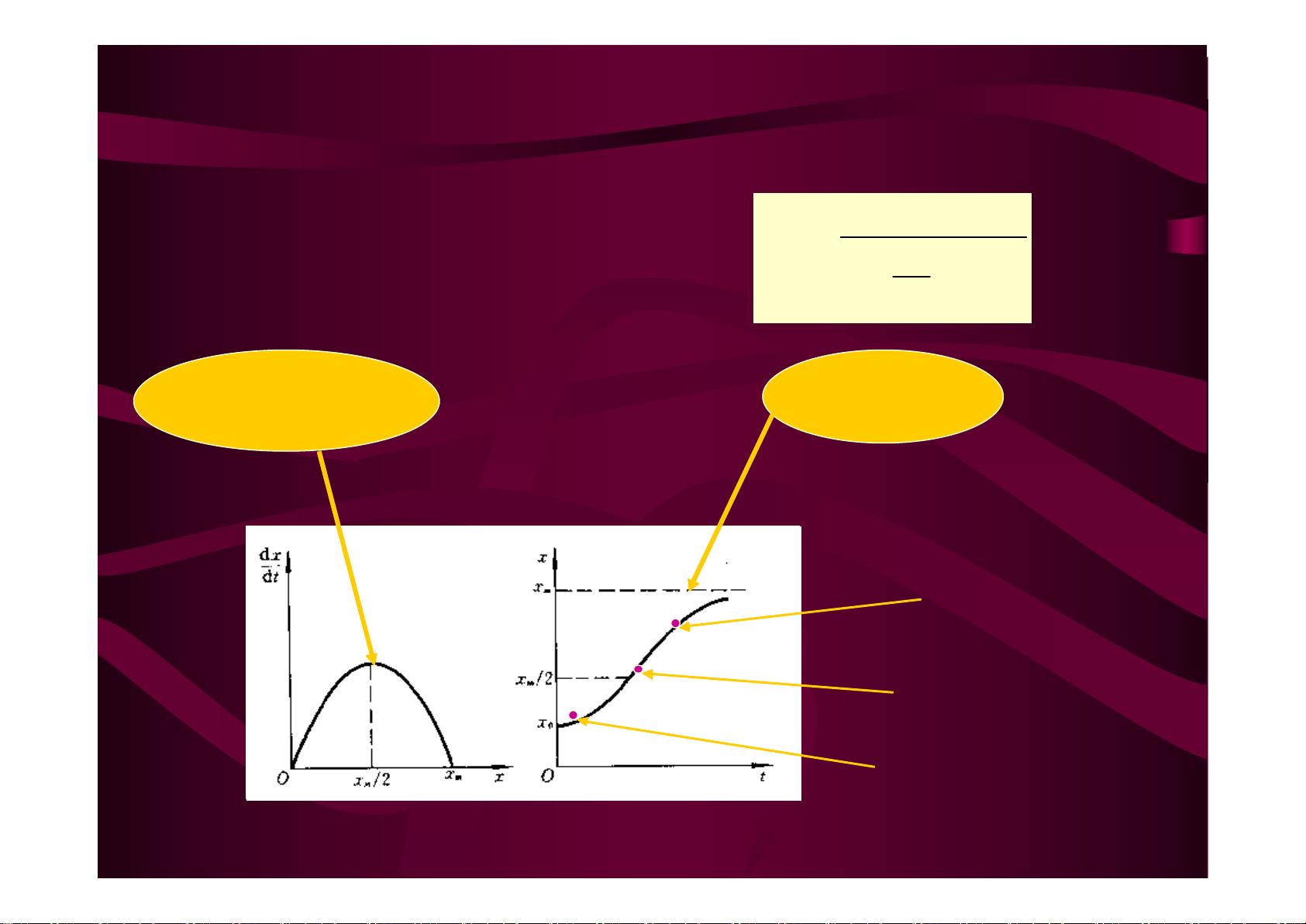
“lesson2（logistic模型与matlab入门）.pdf”是一份关于数学建模和MATLAB应用的教程，主要涉及Logistic模型在人口预报中的应用。该资源包含多种技术项目的源码，适用于不同技术领域的学习者，无论是初学者还是进阶者，可用于毕设、课程设计等多种场景。此外，还鼓励交流和学习，提供问题解答支持。 **数学建模** 数学建模是将实际问题转化为数学模型的过程，通过求解模型并验证其合理性，来解释和解决现实问题。这个过程通常包括问题定义、模型构建、求解、验证和解释结果等步骤。 **Logistic模型** Logistic模型是一种常用于描述有限资源下种群增长的经典模型。它包括两个关键概念：固有增长率（当种群数量很少时的增长率）和环境容纳量（种群可以达到的最大值）。Logistic模型公式表示为：dx/dt = r * x * (1 - x/m)，其中，r是固有增长率，m是环境容纳量，x是当前种群数量。 **模型的解** Logistic模型的解可以通过分离变量法得到，形成一个S形曲线，描述了种群从初始增长到稳定生长的动态过程。在指数增长阶段，种群增长快速，随后逐渐减缓，直到达到环境容纳量。 **参数估计** 估计Logistic模型参数通常采用最小二乘法，通过对历史数据的拟合来确定最佳参数r和m。在MATLAB中，可以编写程序实现这一过程。 **MATLAB应用** 在本教程中，MATLAB被用来处理数据，进行Logistic模型的参数估计和误差分析。例如，通过给定的数据，可以计算出模型的参数并进行误差分析，以确定模型的准确性和适用性。此外，还展示了Logistic模型在水稻叶伸长生长变化和变形虫细胞重量生长等实际问题中的应用。 **课后作业** 作业要求学生使用P11表2的数据，分别确定指数增长模型和Logistic模型的参数，进行误差分析，并编写MATLAB程序。这有助于巩固理论知识并提高实际操作能力。 这份资源提供了丰富的实践机会，让学习者能够深入理解Logistic模型，并掌握如何使用MATLAB进行数学建模和数据分析。对于希望提升这方面技能的人来说，这是一个宝贵的资料库。