深入理解树与二叉树：定义、遍历与应用

"数据结构中的树和二叉树是计算机科学中重要的概念，涉及数据的组织和操作。此资料提供了一套关于树和二叉树的PPT，适合对此领域感兴趣的读者学习。" 树和二叉树是数据结构的基础部分，它们在算法设计、文件系统、编译器设计等多个领域有着广泛应用。 **6.1 树的定义和基本术语** 树是一种非线性的数据结构，由结点和分支组成，形成层次结构。在树中： - **根结点**：树中唯一没有前驱的结点，是整个树的起点。 - **子树**：除了根结点外，其余结点可分成互不相交的子集，每个子集又是一棵树，称为根的子树。 - **结点**：包含数据元素并可拥有零个或多个子树的单元。 - **度**：结点的子树数量，树的度是最大结点度。 - **叶子结点**：没有子树的结点，度为0。 - **分枝结点**：度不为0的结点。 - **路径**：从根到任意结点经过的分支和结点序列。 - **层次**：从根结点开始，根的层次为1，其子节点为2，以此类推。 - **深度**：树中最大层次。 - **有序/无序树**：根据子树的排列顺序区分。 **6.2 二叉树** 二叉树是一种特殊的树结构，每个结点最多有两个子结点，分为左子结点和右子结点。 - **二叉树定义**：如果每个结点最多有两个子结点，那么这样的树称为二叉树。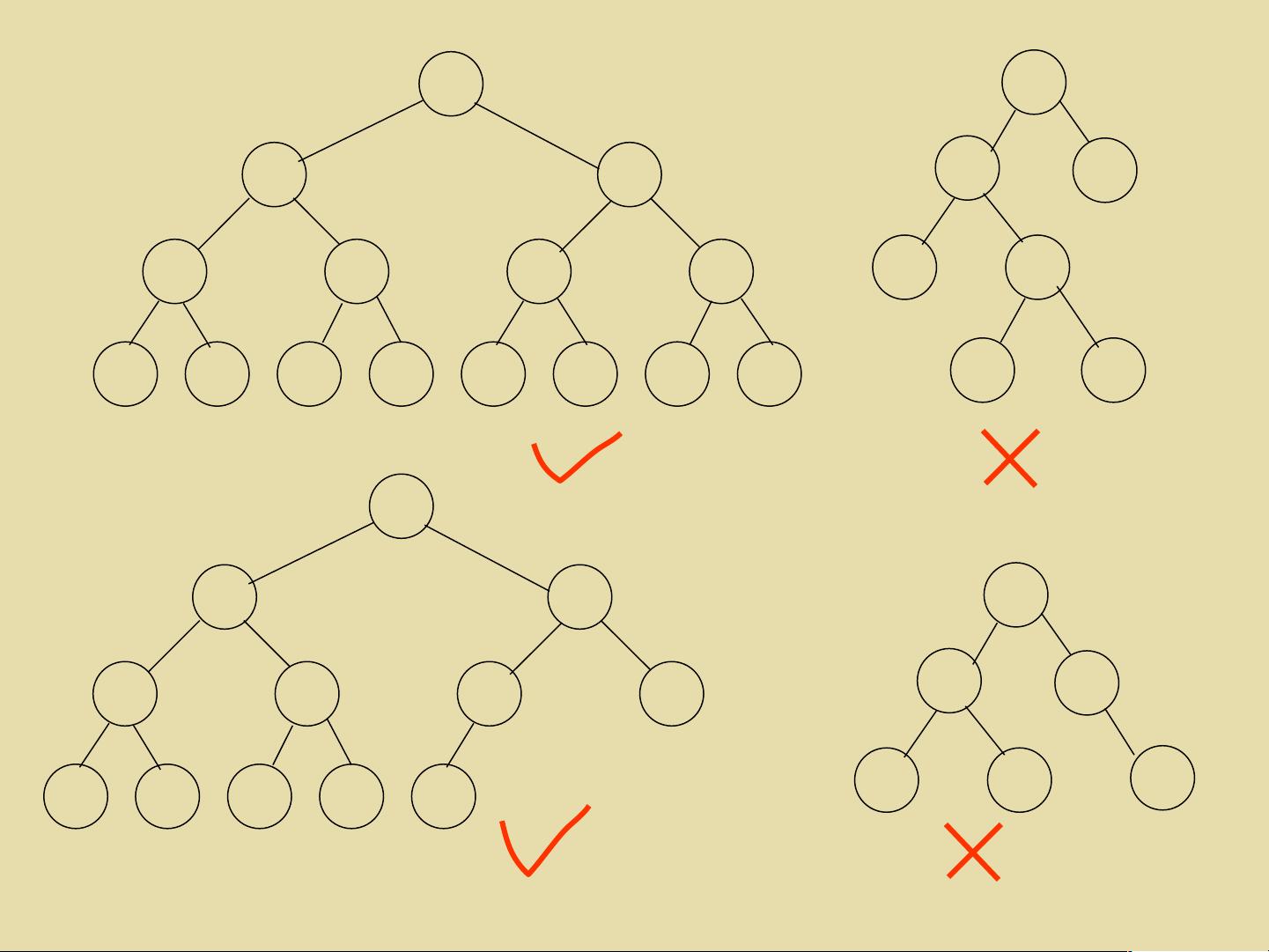 - **二叉树性质**：二叉树有多种特性，如每个结点的子树数量，满二叉树、完全二叉树的概念等。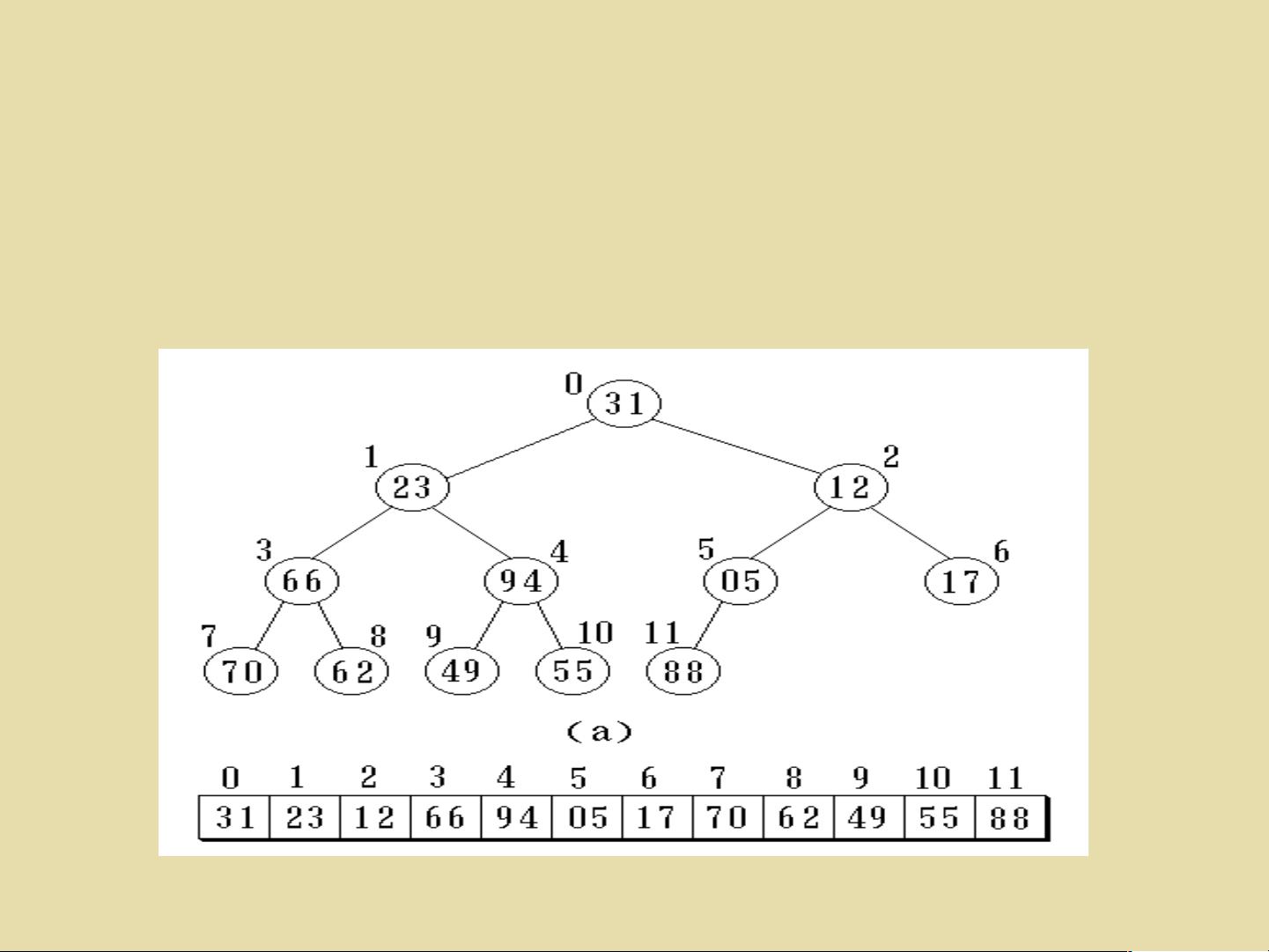 - **二叉树的存储结构**：通常使用数组和链表两种方式来存储二叉树，以便于访问和操作。 **6.3 二叉树的遍历与线索二叉树** - **遍历二叉树**：包括前序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根）。 - **线索二叉树**：通过添加线索指针，使得在二叉链表中可以双向遍历。 **6.4 哈夫曼树及其应用** 哈夫曼树，又称最优二叉树，是一种带权路径长度最短的二叉树，常用于数据压缩和编码。 - **最优二叉树（哈夫曼树）**：构建哈夫曼树的过程是通过合并权值最小的两棵树，直至只剩下一棵树。 - **哈夫曼编码**：根据哈夫曼树生成的编码，具有编码效率高的特点，常用在数据压缩中。 **6.5 树和森林** - **树的存储结构**：可以采用链接结构或者数组结构存储树。 - **森林与二叉树的转换**：通过一定规则，森林和二叉树之间可以相互转换。 - **森林的遍历**：类似树的遍历，对森林中的每棵树进行遍历。 树和二叉树是数据结构中至关重要的一部分，它们提供了高效处理和组织数据的方式。理解并熟练掌握这些概念，对于解决实际问题具有很大的帮助。