深度学习中的主成分分析PCA详解
需积分: 15 63 浏览量
更新于2024-07-17
收藏 4.72MB PDF 举报
"本资源是一份关于主成分分析(PCA)的详细讲解材料,旨在帮助学习者快速入门并深入理解PCA的实际应用。"
在机器学习和数据分析领域,主成分分析(Principal Component Analysis, PCA)是一种常用的数据降维技术。PCA的主要目标是通过线性变换将高维数据转换到低维空间,同时保持数据集中的方差尽可能大。这有助于减少数据的复杂性,提高模型的效率,并且在可视化、去除噪声以及后续机器学习算法处理等方面具有显著优势。
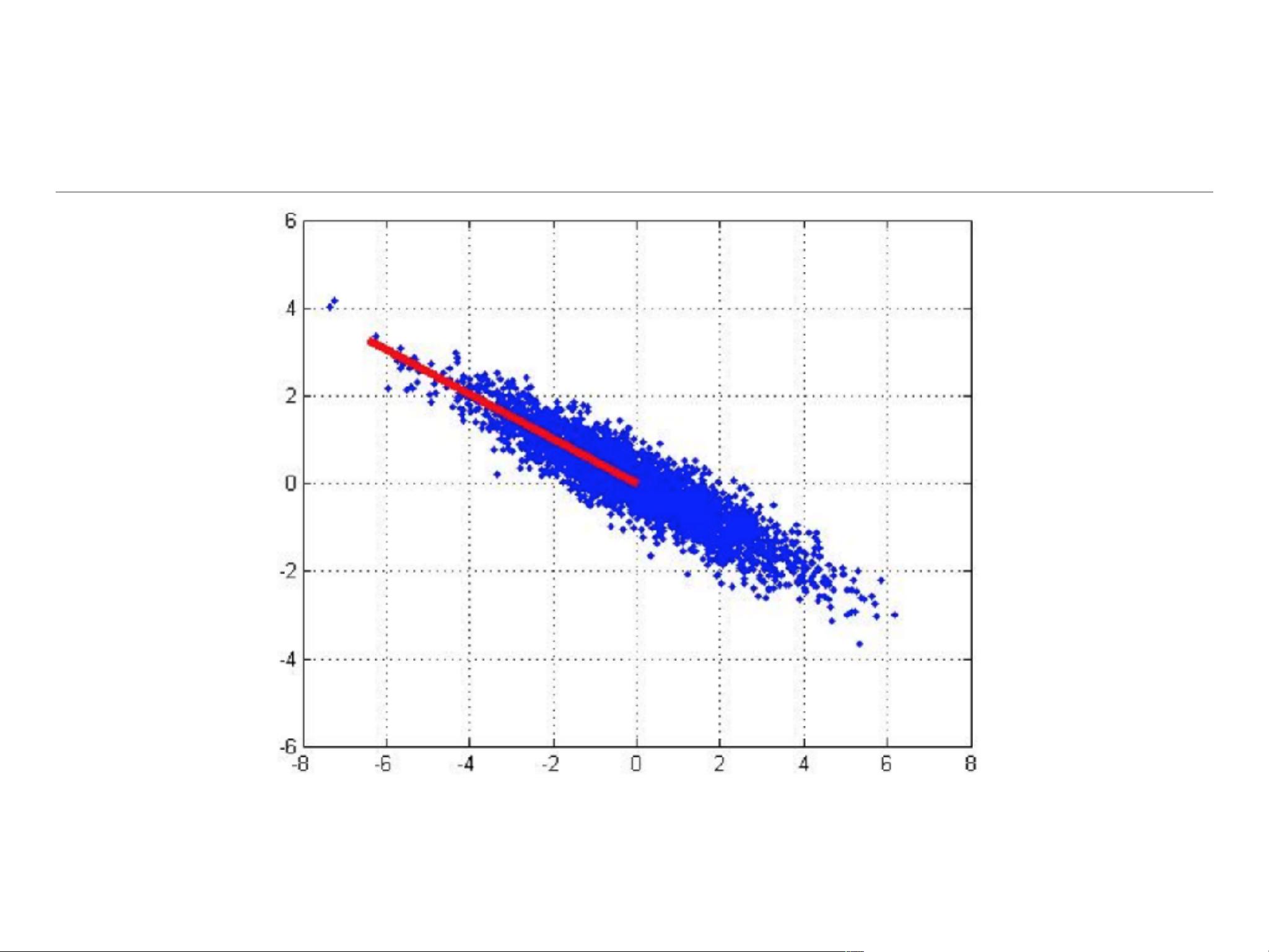
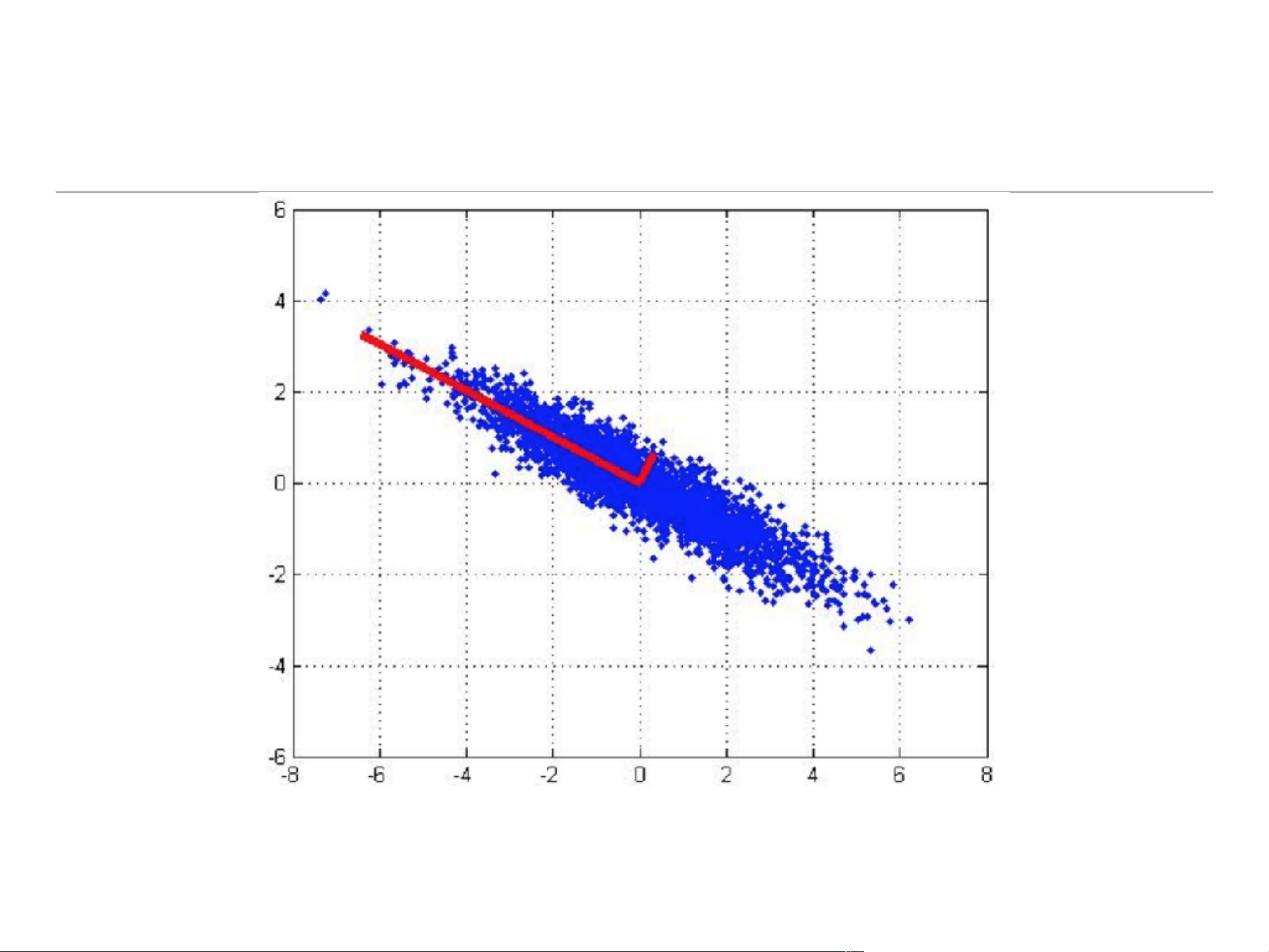
PCA首先通过对原始数据进行标准化处理,确保所有特征在同一尺度上。接着,它寻找数据集的主要方向,这些方向被称为主成分,它们是数据方差最大的方向。第一主成分解释了数据方差的最大部分,第二主成分在与第一主成分正交的方向上解释了剩余方差的最大部分,以此类推。通过选择前k个主成分,可以构建一个k维子空间,该子空间保留了原始数据的大部分信息,但维度大大降低。
PCA的应用广泛,例如在文档分类中,面对成千上万个单词或词组,PCA可以帮助我们找到最具代表性的特征;在Netflix用户调查数据中,PCA可以降低用户和电影之间的维度,使分析更高效;在脑影像学研究中,PCA可以处理大量的时空数据,提取关键模式;在图像处理中,PCA可用于压缩图像,减少像素数量而不失重要信息。
PCA的例子通常包括对图像数据的处理,如将200x300像素的图像降维到更低的维度,同时保持图像的主要特征。此外,PCA还可以与其他无监督学习方法如核PCA和独立成分分析(ICA)结合,用于发现隐藏的低维结构。
PCA的优势在于:
1. 可视化:低维表示更容易被人类理解和可视化。
2. 资源效率:减少计算量,提高处理速度。
3. 统计效果:减少维度通常能提高模型的泛化能力。
4. 噪声去除:通过降维,可以去除部分噪声,提高数据质量。
5. 机器学习预处理:降维后的数据更适合输入到其他机器学习算法中。
然而,PCA也有其局限性,如假设数据线性可分,可能不适用于非线性问题,以及可能会丢失某些非主要但重要的信息。在实际应用中,需要根据具体问题选择合适的数据降维方法。
PCA是一种强大的工具,尤其适用于处理高维数据,它能够简化数据结构,提高分析效率,同时也为后续的机器学习任务提供更优的输入。通过深入理解PCA的原理和应用场景,我们可以更好地应对各种数据分析挑战。
2018-04-10 上传
2009-11-24 上传
2011-02-21 上传
2022-06-14 上传
2022-05-30 上传
2022-01-06 上传
2021-09-26 上传
2021-07-03 上传
2019-10-19 上传
qq_38264395
- 粉丝: 0
- 资源: 6
最新资源
- 第10章 实战Smart Forms设计.pdf
- 第9章 Tree Control的使用.pdf
- 毕业设计psk调制解调资料
- 第8章 ALV控件的使用.pdf
- 第7章 表控制Table Control设计.pdf
- 第6章 实战屏幕SCREEN设计.pdf
- 单片机教程(C 语言入门)
- 第5章 标准列表和选择屏幕.pdf
- Struts快速学习指南.pdf
- GDI+ SDK参考(翻译版本)
- 第4章 数据字典和数据表的读取.pdf
- usb規範1.1 中文版
- Windows CE短消息API的使用
- 第3章 ABAP语法示例.pdf
- 第2章 创建HELLO WORLD程序
- 第1章 ABAP开发环境和总体介绍