相关与回归分析：理解相关系数与一元线性回归

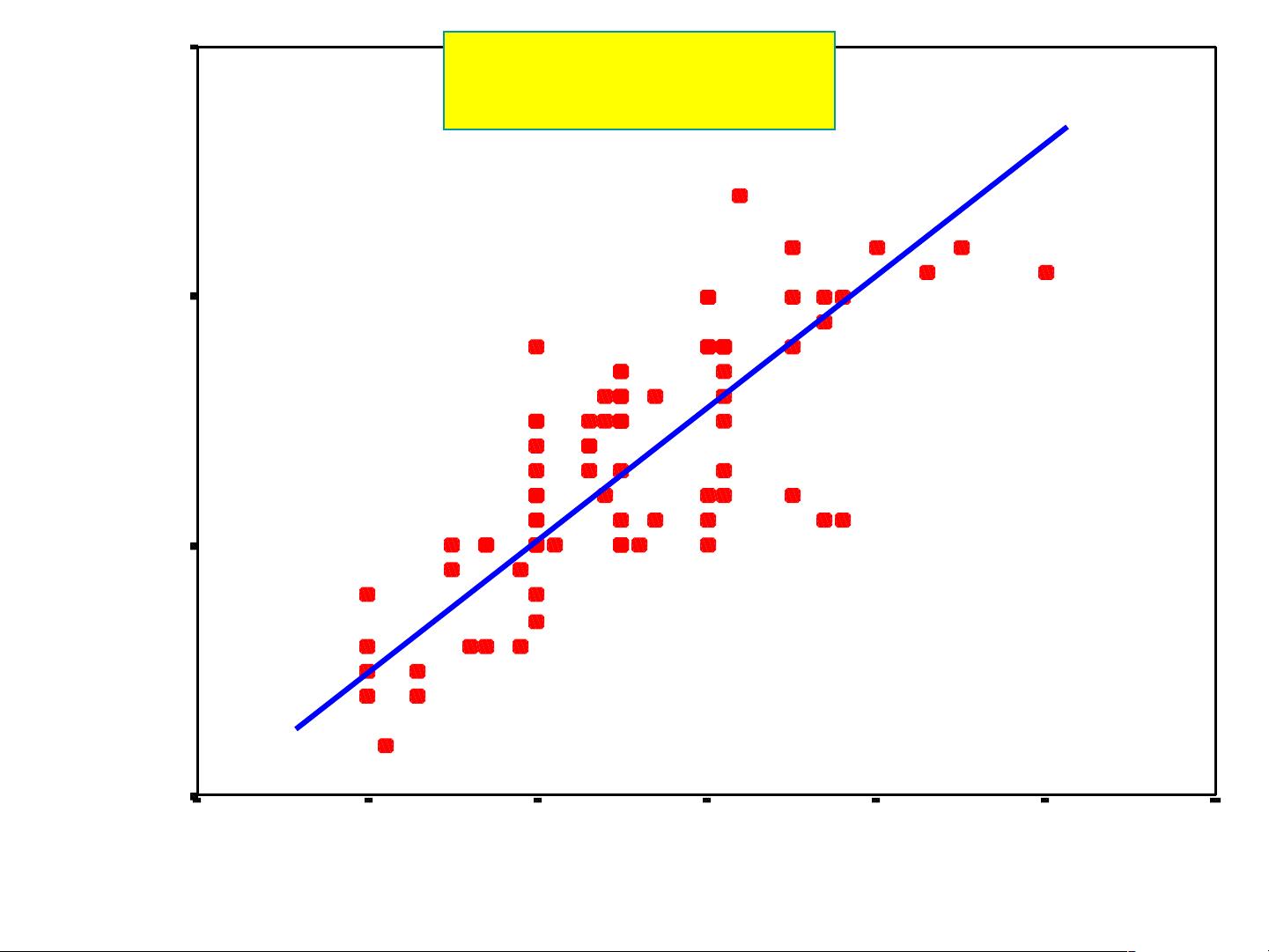
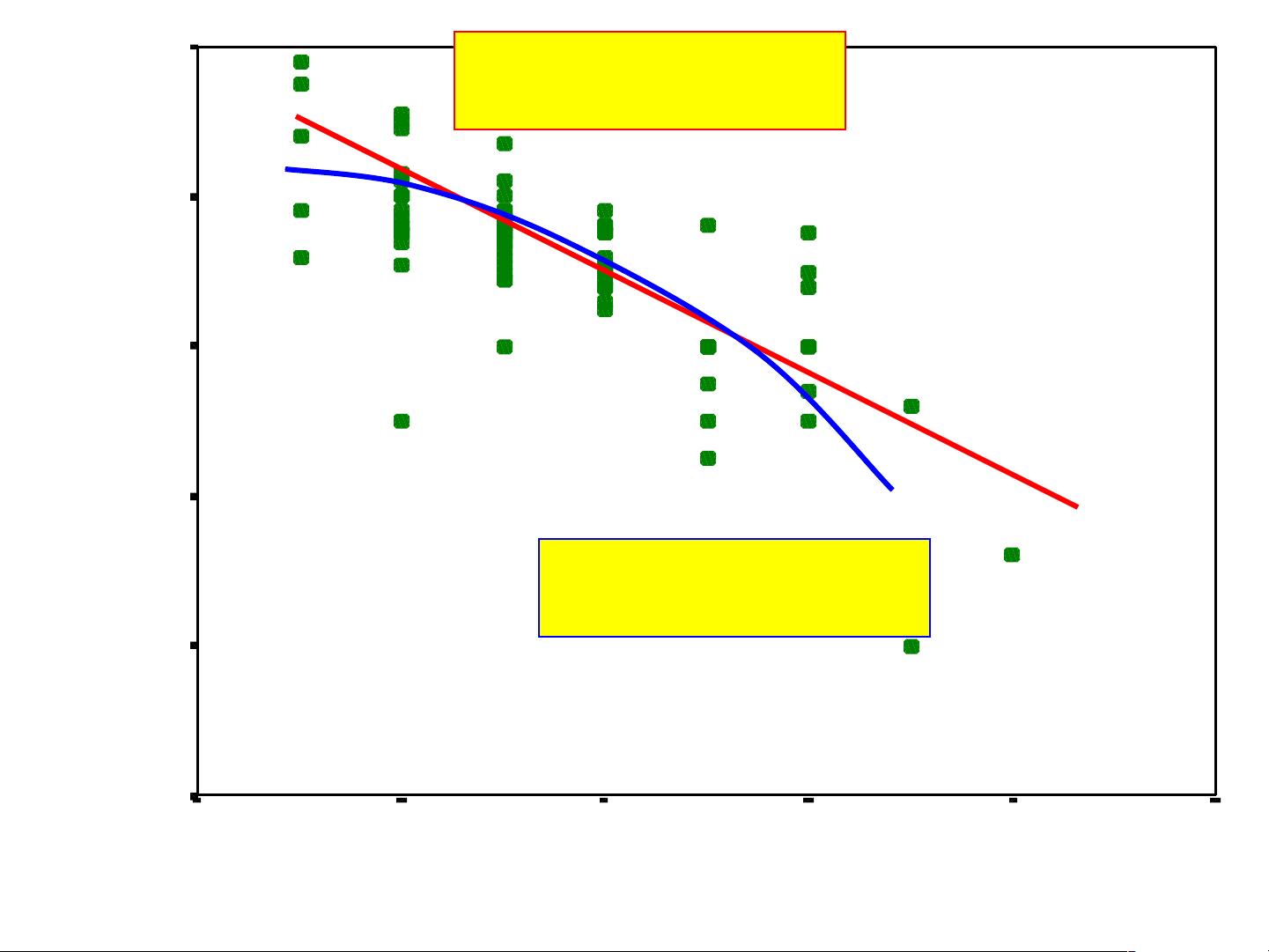
"第七章 相关和回归分析.ppt - 精品文档" 相关分析与回归分析是统计学中的重要概念，它们被广泛应用于社会科学、经济学、医学研究以及各种工程领域，用来研究两个或多个变量之间的关系。相关分析关注的是变量间的关联程度，而回归分析则致力于建立一个数学模型，以描述这种关系并进行预测。 一、相关分析 相关分析的核心是相关系数，它衡量的是两个变量之间的线性关系强度和方向。相关系数的取值范围在-1到1之间，正值表示正相关（一个变量增加时，另一个也倾向于增加），负值表示负相关（一个变量增加时，另一个减少）。当相关系数接近0时，意味着变量间的关系较弱或不存在明显的线性关系。计算相关系数通常使用皮尔逊积矩相关系数，但需要注意的是，相关系数只能衡量线性关系，并不能反映非线性关联。 二、回归分析 1. 一元线性回归：在一元线性回归中，我们探讨一个自变量（X）如何影响一个因变量（Y）。目标是找到一条直线（回归线），使得所有数据点到这条直线的距离平方和最小，这称为最小二乘法。回归线的方程式通常表示为 Y = a + bX + ε，其中a是截距，b是斜率，ε是随机误差项。通过这种方法，我们可以估计当自变量变化一个单位时，因变量平均变化的量。 2. 参数估计：回归分析的关键步骤之一是对回归方程中的参数进行估计。常用的方法是极大似然估计和最小二乘估计。最小二乘估计是最常用的，因为它计算简便且对异常值相对不敏感。 3. 回归方程的显著性检验：检验回归方程的整体显著性通常采用F检验，而检验斜率b的显著性则使用t检验。这些检验帮助我们判断自变量是否对因变量有统计意义上的显著影响。 4. 预测与应用：一旦建立了有效的回归模型，就可以用于预测未知数据点的因变量值。例如，在经济学中，通过历史的消费支出和收入数据，可以构建回归模型预测未来的消费趋势。 相关分析和回归分析是相辅相成的。相关分析可以帮助我们初步了解变量间的关系强度，而回归分析则进一步深入，构建数学模型来量化这种关系并进行预测。然而，这两者都有其局限性，如无法揭示因果关系，只适用于线性关系，以及可能受到异常值和多重共线性等因素的影响。因此，在实际应用中，我们需要结合其他统计方法和领域知识，以全面理解数据背后的现象。