维纳与卡尔曼滤波简介及MATLAB实现

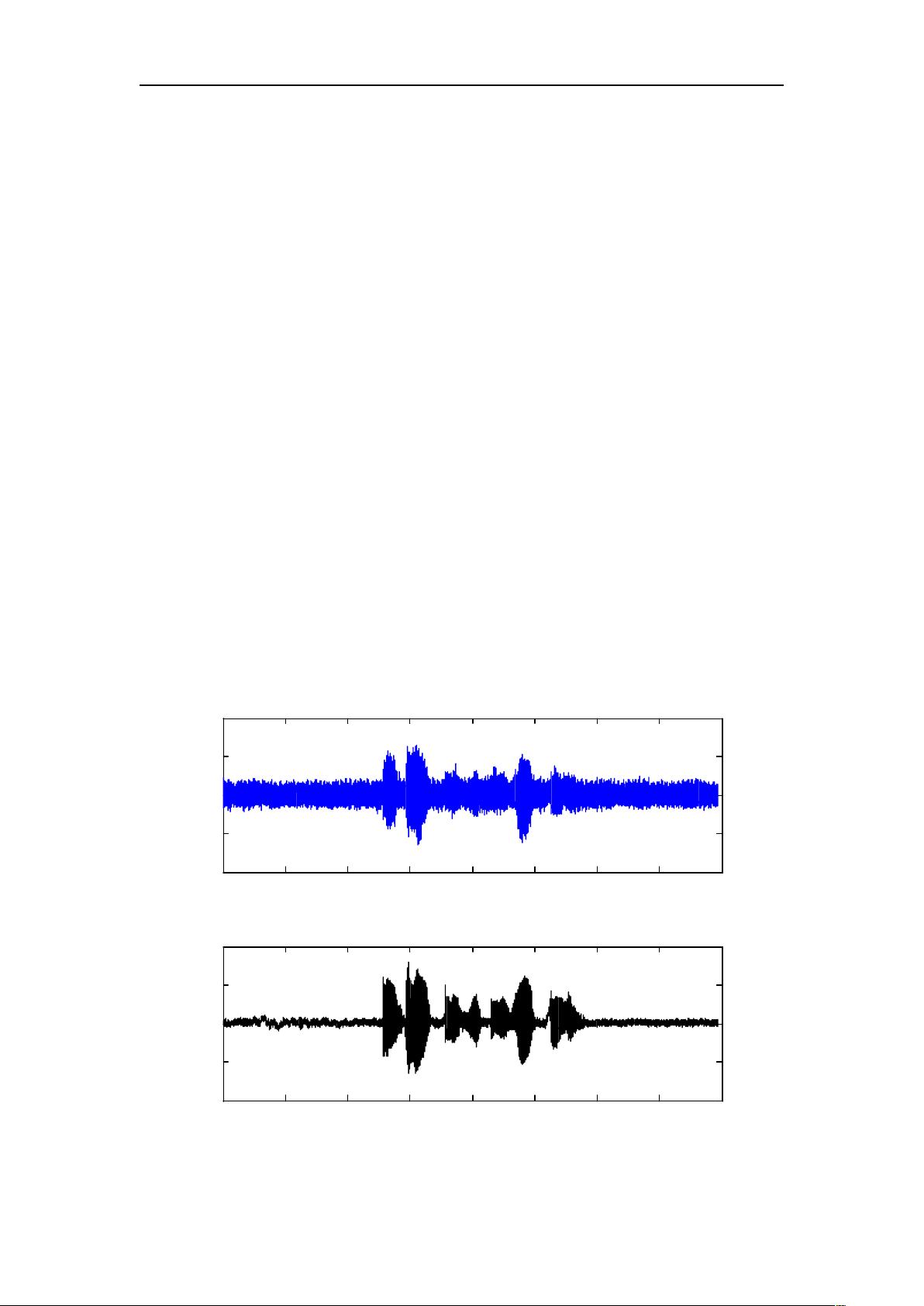
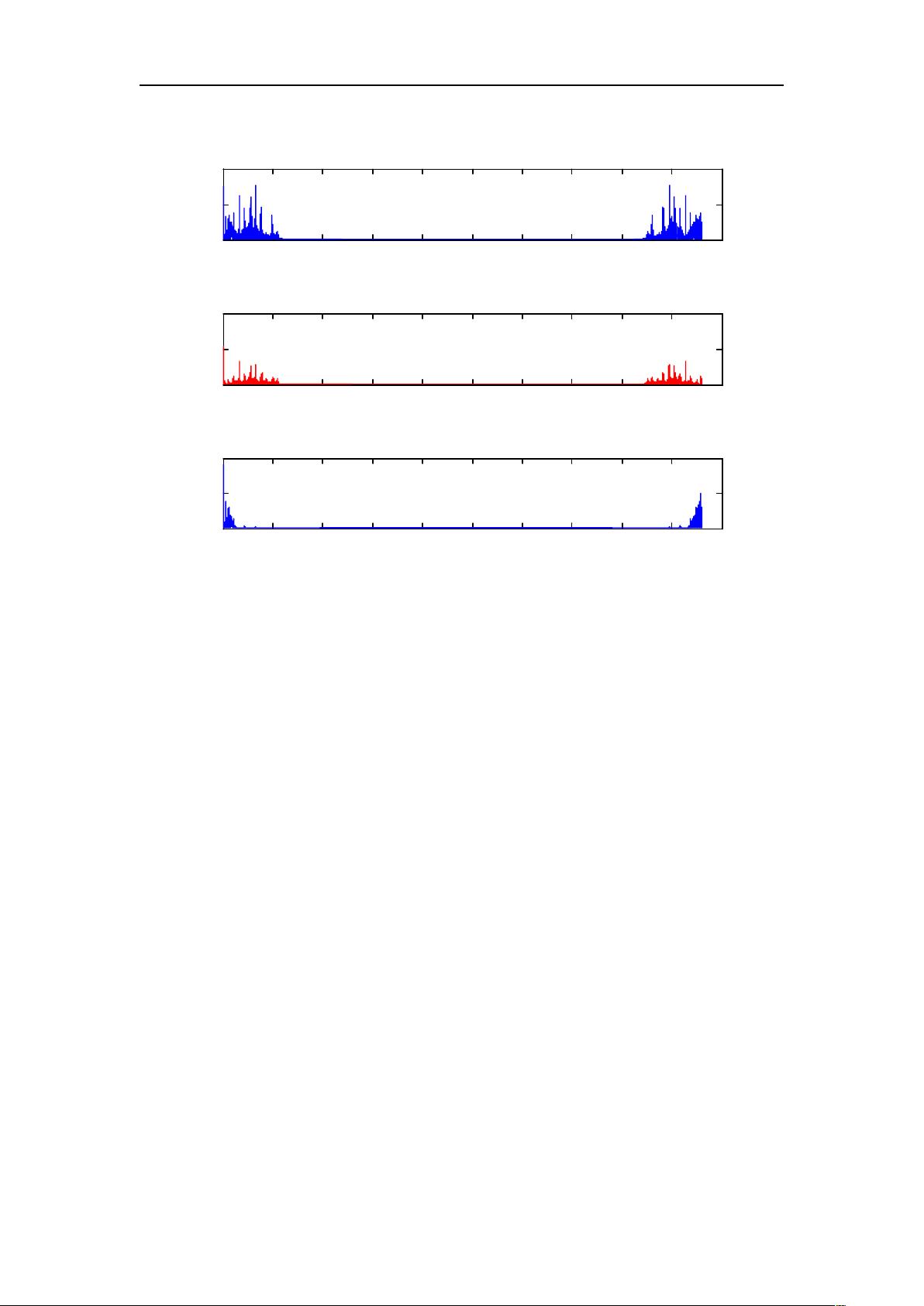
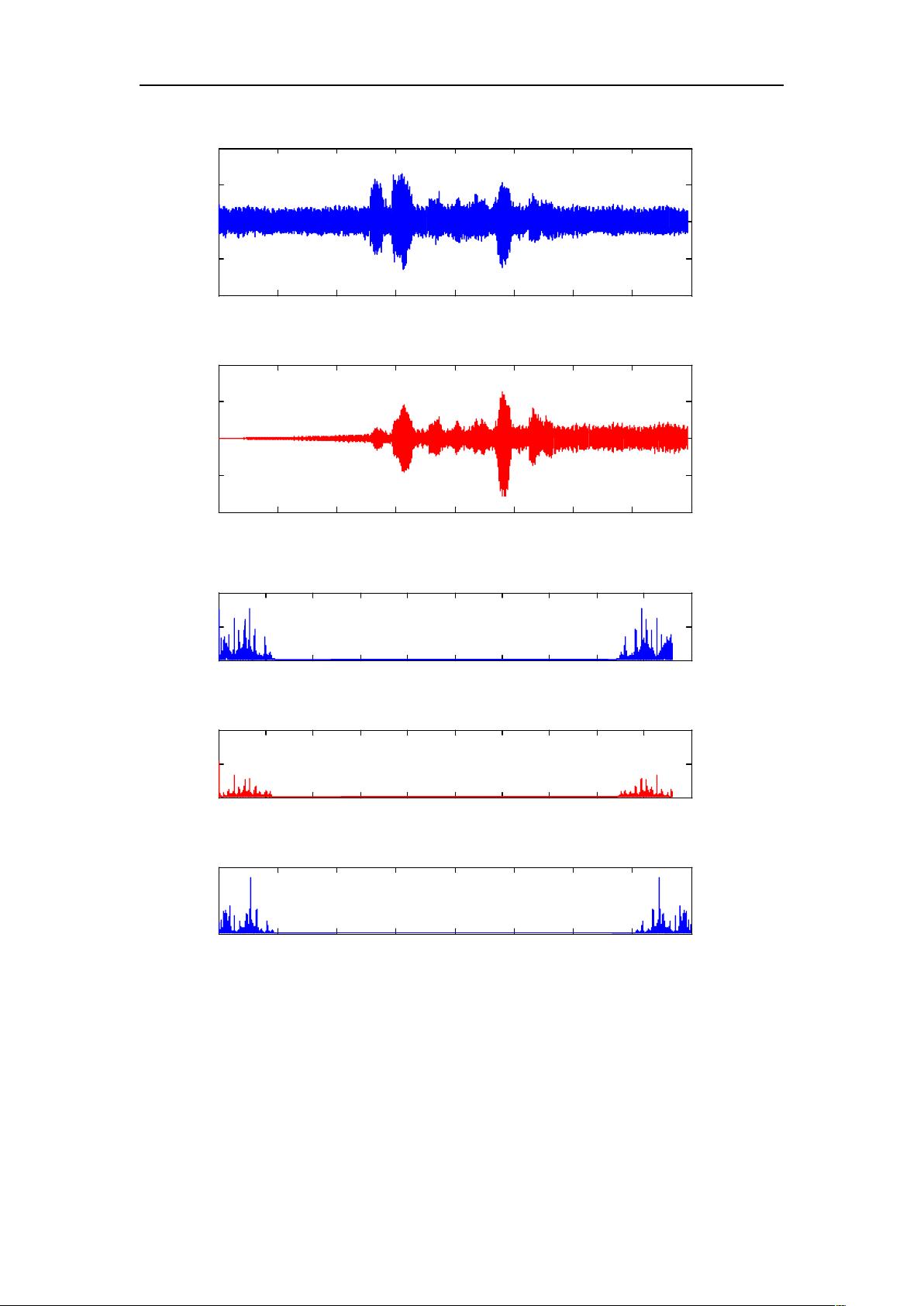
"本文档介绍了维纳滤波和卡尔曼滤波的基本概念，并提供了MATLAB实现的示例。文档首先阐述了维纳滤波的原理，指出其在噪声信号分离中的应用，然后通过MATLAB代码对比了维纳滤波与均值滤波的效果。接着，文档展示了维纳滤波在图像复原中的应用，以及如何处理运动模糊和噪声的图像。" 维纳滤波是一种基于最小均方误差准则的滤波方法，主要目的是从含有噪声的信号中恢复出原始信号。它假设输入信号为含噪声的随机过程，通过计算最优冲激响应来最小化均方误差，从而达到最佳滤波效果。维纳滤波器适用于连续或离散、标量或向量的平稳随机过程，但实际应用中往往受限于需要长时间段的数据以及对非平稳噪声的处理能力。 在MATLAB中，可以使用`wiener2`函数实现二维维纳滤波。文档提供的示例中，将维纳滤波应用于含高斯噪声的图像`lena.bmp`，并与均值滤波进行了比较。均值滤波通过移动窗口内的像素平均值进行平滑，而维纳滤波则考虑了噪声统计特性，通常能更好地保留图像细节。 在图像复原部分，文档演示了如何使用维纳滤波恢复经过运动模糊的图像。首先生成了模拟运动模糊的图像，然后应用维纳滤波器进行复原。此外，还添加了随机噪声来模拟真实世界中的复杂情况，进一步展示了维纳滤波在处理噪声时的性能。 卡尔曼滤波是一种在线性高斯系统中，基于预测和更新步骤的最优估计方法，尤其适用于动态系统的状态估计。虽然在文档中未详细展开，卡尔曼滤波器通常用于实时估计随时间变化的系统状态，例如目标跟踪、导航系统等。在MATLAB中，可以使用`kalman`函数来实现卡尔曼滤波算法。 总结来说，维纳滤波和卡尔曼滤波是两种重要的信号和图像处理工具，前者适用于静态信号的噪声去除，后者适用于动态系统的状态估计。在实际应用中，选择合适的滤波方法取决于具体的问题需求和数据特性。MATLAB提供了丰富的工具和函数，使得这些复杂的滤波算法得以方便地实现和测试。