"数据结构与算法查找: 顺序、折半、分块和树表查找综述"
下载需积分: 9 | DOCX格式 | 11.26MB |
更新于2024-01-15
| 42 浏览量 | 举报
数据结构与算法中的查找是指在给定的数据集合中寻找特定元素的过程。查找算法是计算机程序设计中的基础技术,广泛应用于各个领域。本文将介绍常见的几种查找算法,包括顺序查找、折半查找、分块查找、二叉排序树查找和散列表查找,并对它们的特点和性能进行分析。
一、引入:
查找的目的是为了在一个数据集合中找到特定的元素。根据查找的分类,可以将查找分为线性表的查找和树表的查找两类。线性表的查找适用于有序或无序的数据集合,而树表的查找适用于经过组织的数据结构。
二、线性表的查找:
1.顺序查找:
顺序查找是最简单的查找算法之一,它的实现思路是从数据集合的第一个元素开始逐个比较,直到找到目标元素或遍历完整个集合。顺序查找的时间复杂度为O(n),其中n是数据集合的大小。
注意:由于每次 for 循环都需要比较两次,因此可以使用改进方法来提高时间效率。改进方法是将目标元素放在数组的首位,这样不需要每次循环都比较两次。
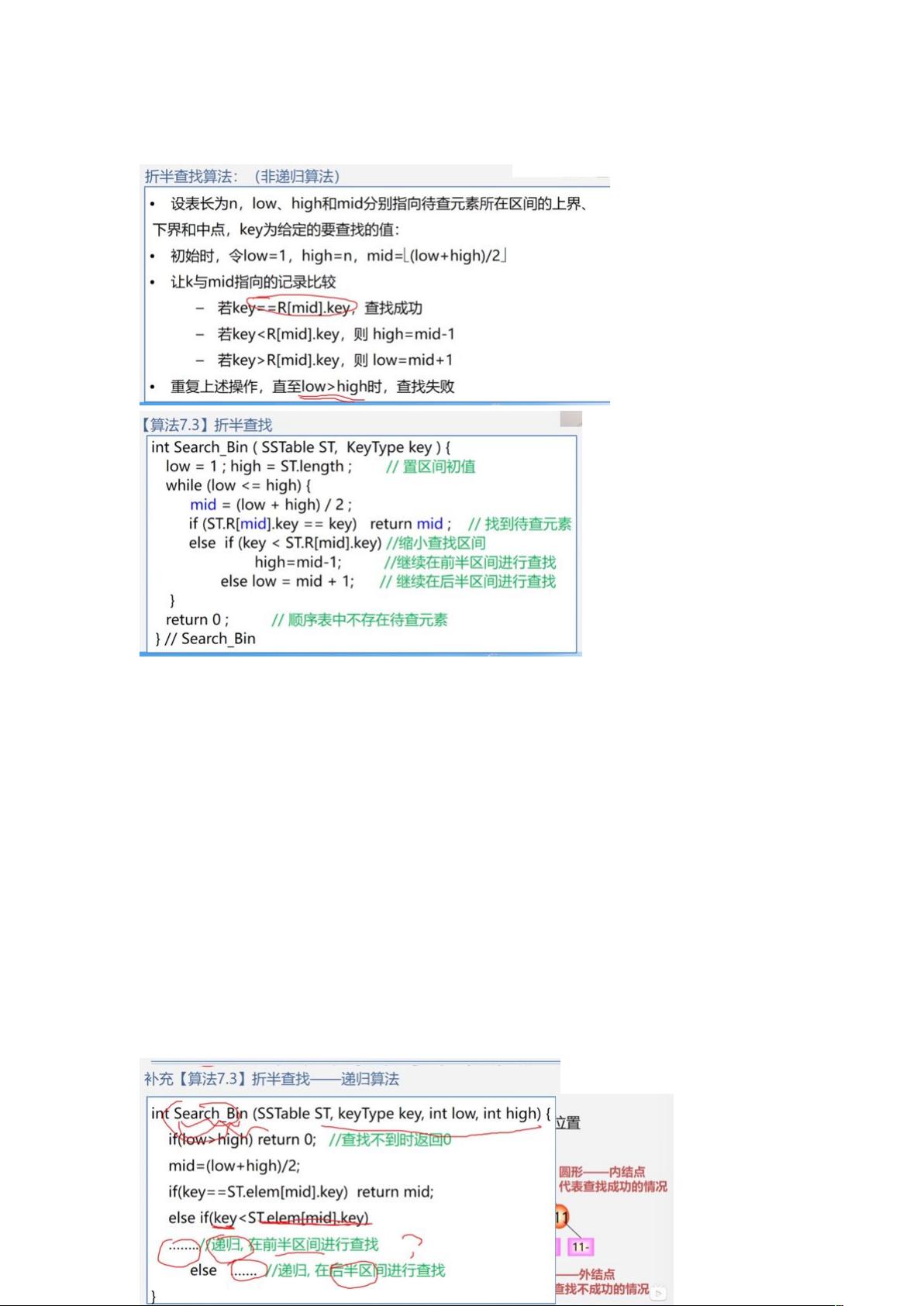
2.折半查找(二分查找):
折半查找是一种更高效的查找算法,适用于有序数据集合。它的实现思路是将数据集合分成两半,然后比较目标元素和中间元素的大小,继续在较小或较大的一半中查找,直到找到目标元素或无法继续分割。折半查找的时间复杂度为O(log n),其中n是数据集合的大小。
非递归算法的折半查找使用迭代的方式实现,递归算法使用递归的方式实现。折半查找的性能分析包括查找树的构建和查找路径的长度计算。举例来说,有一个包含100个有序元素的数据集合,折半查找最多只需要7次比较。
3.分块查找:
分块查找是在一个分块有序的数据集合中进行查找。分块查找的思路是将数据集合按照一定的块大小分成多个块,每个块内部是有序的,但不要求整个数据集合是有序的。通过先在块内查找,再在块间查找的方式找到目标元素。分块查找的性能分析与块的大小有关,一般情况下,分块查找的时间复杂度介于O(1)和O(log m)之间,其中m是块的数量。
树表的查找:
1.二叉排序树:
二叉排序树是一种有序的二叉树,左子树的所有节点的值小于根节点,右子树的所有节点的值大于根节点。通过中序遍历二叉排序树,可以获得一个有序的序列。在二叉排序树中查找一个元素的思路是从根节点开始,根据节点的值和目标元素的大小关系,逐步向左子树或右子树查找,直到找到目标元素或遍历完整个二叉树。二叉排序树的查找时间复杂度与树的高度相关,平均情况下为O(log n),其中n是节点的数量。
2.平衡二叉树:
平衡二叉树是一种高度平衡的二叉排序树,通过调整节点的位置保持整棵树的平衡性。平衡二叉树的调整方法主要有RR型、LL型和RL型三种。RR型是指节点的右子树的右子树上出现失衡,LL型是指节点的左子树的左子树上出现失衡,RL型是指节点的右子树的左子树上出现失衡。通过对平衡二叉树进行调整,可以保证树的高度在一定范围内,从而提高查找的效率。
3.散列表查找:
散列表是一种根据关键字直接进行访问的数据结构,可以用于快速的查找。散列表的构造包括散列函数的构造和冲突处理方法的选择。常用的散列函数有直接定址法和除留余数法。直接定址法是根据关键字的值直接计算其存储位置,除留余数法是将关键字的值除以某个数并取余数作为存储位置。处理冲突的方法有开放地址法和链地址法。开放地址法是在散列表中寻找空的位置来存储冲突的元素,链地址法是将冲突的元素存储在链表中。可以根据具体的需求选择合适的散列函数和冲突处理方法。
综上所述,查找是数据结构与算法中的核心技术之一。不同的查找算法适用于不同的数据集合和需求。选择合适的查找算法可以提高查找的效率和性能。通过掌握和应用不同的查找算法,可以更好地解决实际问题。
相关推荐








redlantern红灯笼
- 粉丝: 103
最新资源
- 多功能字模信息获取工具应用详解
- ADV2FITS开源工具:视频帧转换为FITS格式
- Tropico 6内存读取工具:游戏数据提取与分析
- TcpUdp-v2.1:便捷网络端口管理小工具
- 专业笔记本BIOS刷新软件InsydeFlash 3.53汉化版
- GridView中加入全选复选框的客户端操作技巧
- 基于JAVA和ORACLE的网吧计费系统解决方案
- Linux环境下Vim插件vim-silicon:源代码图像化解决方案
- xhEditor:轻量级开源Web可视化HTML编辑器
- 全面掌握Excel技能的视频课程指南
- QDashBoard:基于QML的仪表盘开发教程
- 基于MATLAB的图片文字定位技术
- Proteus万年历仿真项目:附源代码与Proteus6.9SP4测试
- STM32 LED实验教程:点亮你的第一个LED灯
- 基于HTML的音乐推荐系统开发
- 全中文注释的轻量级Vim配置教程