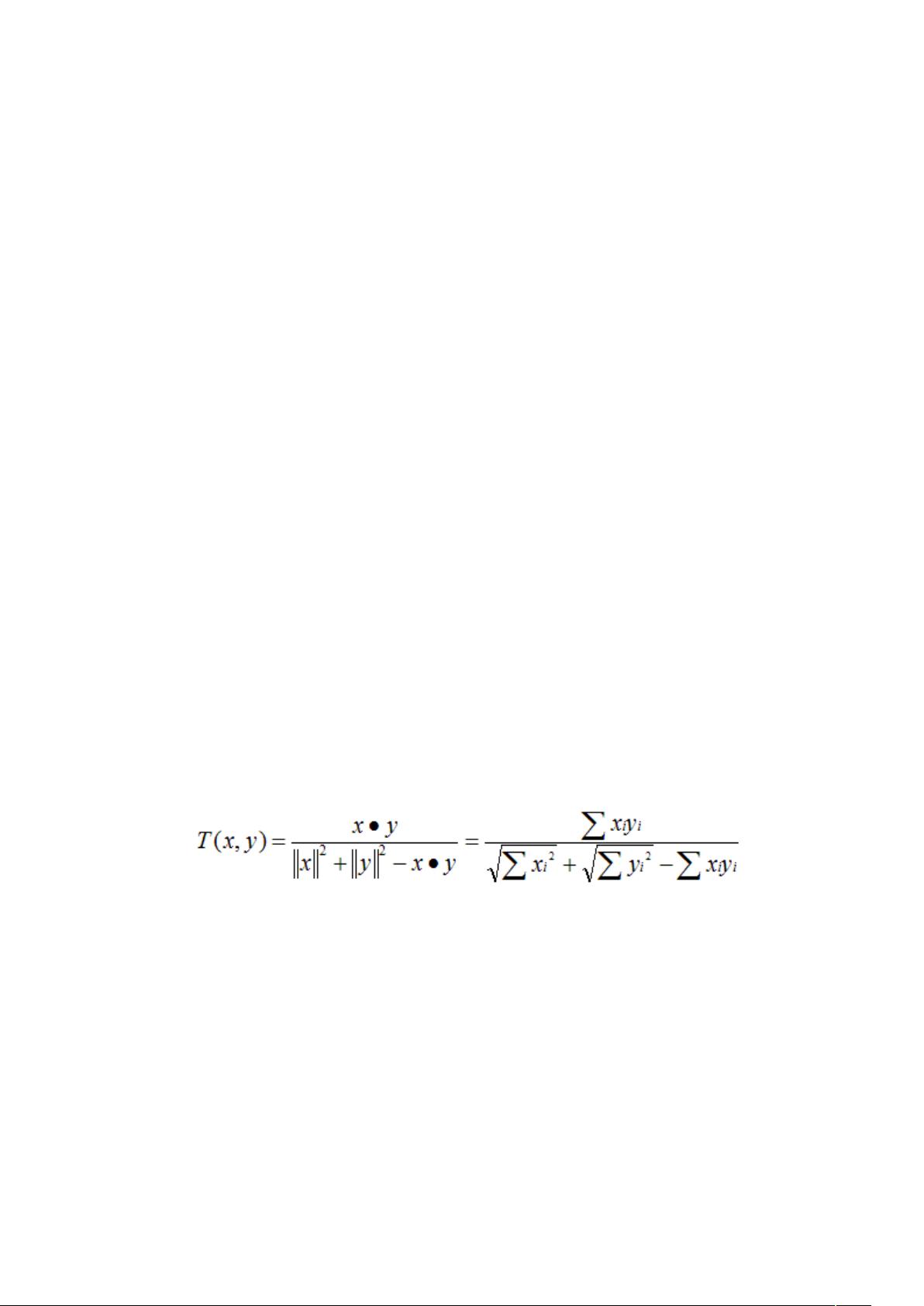基于向量的相似度计算方法：皮尔逊、欧几里德与余弦相似度

"本文主要介绍了相似度计算的基本概念和几种常用的方法，包括皮尔逊相关系数、欧几里德距离以及余弦相似度，并详细解释了它们的原理、适用范围和局限性。" 相似度计算在信息技术领域中扮演着重要角色，尤其是在推荐系统、文本挖掘和数据分析中。它用来衡量两个数据对象间的相似程度或关联性。通常，这些方法基于向量表示，通过计算向量之间的距离来评估相似性。以下是对几种常见相似度计算方法的详细说明： 1. **皮尔逊相关系数**（Pearson Correlation Coefficient）： - 皮尔逊相关系数是衡量两个变量间线性关系强度和方向的统计指标，其值在-1到1之间。 - 类名：PearsonCorrelationSimilarity - 原理：计算两个变量的协方差与它们的标准偏差的乘积。 - 范围：[-1, 1]，正值表示正相关，负值表示负相关，绝对值越大，相关性越强。 - 局限性：不考虑重叠数量，仅适用于等间距的成对正态分布数据。 2. **欧几里德距离**（Euclidean Distance）： - 欧几里德距离是多维空间中两点间的直线距离。 - 类名：EuclideanDistanceSimilarity - 原理：通过1/(1+d)公式将距离转换为相似度，其中d为欧几里德距离。 - 范围：[0, 1]，值越大，相似度越高。 - 局限性：同样忽略了重叠数的影响， Mahout通过添加Weighting参数来解决这个问题。 3. **余弦相似度**（Cosine Similarity）： - 余弦相似度常用于文本分析，衡量向量间的夹角余弦，而非直接距离。 - 原理：计算两个向量的内积除以它们的模长乘积。 - 优势：不受向量长度影响，仅关注向量的方向。 - 应用：在信息检索和文档分类中，用于找出主题相似的文档。 除了上述方法，还有其他相似度计算方法，如Jaccard相似度（用于集合数据）、曼哈顿距离（Manhattan Distance）和切比雪夫距离（Chebyshev Distance）。选择哪种方法取决于具体的应用场景和数据特性。例如，皮尔逊相关系数适合连续变量，欧几里德距离适用于数值型数据，而余弦相似度则在处理高维稀疏数据时表现出色。 在实际应用中，可能需要结合多种相似度计算方法，或者进行适当的调整以适应特定问题。比如，通过调整权重来考虑重叠数量，或者使用归一化来消除尺度影响。同时，对于非数值型数据，可能需要先进行编码或转化，如TF-IDF变换，才能使用这些相似度度量。 理解和选择合适的相似度计算方法是理解和优化机器学习模型的关键步骤，它能够有效地揭示数据间的内在联系，为决策提供有力的支持。