使用LHS和YIQ的高效色彩图像gamut裁剪技术

需积分: 5 126 浏览量更新于2024-08-04 收藏 545KB PDF 举报

"这篇论文探讨了在颜色图像处理中使用LHS（Lightness, Hue, Saturation）和YIQ色彩空间进行高效色域剪裁的策略。文章详细介绍了如何在这些色彩空间中调整图像的饱和度和亮度，并且在RGB色彩范围之外快速执行色域剪裁。这种方法在显示设备和摄影应用中都有广泛的应用。" 在图像处理领域，色域剪裁（Gamut Clipping）是一项关键的技术，它涉及到当颜色值超出可显示或可打印的色域范围时，如何适当地处理这些超出范围的颜色。高效的色域剪裁对于确保图像在不同设备间的一致性和避免颜色失真至关重要。 LHS色彩空间是基于亮度（Lightness）、色调（Hue）和饱和度（Saturation）的一种色彩表示方法，它与人眼对颜色的感知更接近，因此在处理颜色时更为直观。在LHS空间中进行色域剪裁，可以更精确地控制图像的色彩表现，同时保持色调的连续性，避免因为剪裁导致的色彩跳跃。 YIQ色彩空间则常用于电视和通信系统中，因为它易于转换自RGB空间，且便于调制传输。在YIQ空间进行色域剪裁，可以更好地适应不同的显示条件，特别是在处理电视或视频信号时，能确保颜色的正确显示。论文《Efficient gamut clipping for color image processing using LHS and YIQ》由Christopher C. Yang和S.H. Kwok共同撰写，发表于2003年的《Optical Engineering》杂志上。两位作者都是在图像处理和工程管理领域的专家。他们提出的算法能够有效地解决超出RGB色域的问题，确保图像在处理后仍保持良好的视觉效果。该论文受到了63次引用，阅读量达到了1,858次，表明其在学术界和工业界具有较高的影响力。Christopher C. Yang，作为该论文的作者之一，还从事着其他相关项目的研究，如主动视觉检测中的误差分析和与怀孕相关的OUD研究。这篇论文提供的色域剪裁方法在实际应用中具有很高的价值，无论是在图像增强、显示设备校准还是摄影后期处理中，都能帮助处理颜色溢出问题，从而提高图像的质量和一致性。

• orthogonal clipping 共to the boundary of the gamut兲

• cusp clipping or chord clipping

• mapping functions, e.g., sigmoid lightness mapping

function and chroma mapping function

• categorical mapping.

Next are some recently developed clipping techniques.

Ito, Katoh, and Ohno

7,8

proposed to clip the out-of-

gamut color to the reproduction gamut boundary. The

smallest E value calculated by a weighted color difference

formula CIELAB is employed. Other color difference for-

mulas, ⌬E

⌬E

CMC

⌬E

BFD

and

⌬E

were also studied. Braun and Fairchild investigated

the hue nonuniformities in CIELAB

and developed the

sigmoidal lightness mapping functions to boost the image

contrast selectively when the original gamut is mapped into

the reproduced gamut.

Shimizu et al.

proposed the

chroma proportional clipping 共CPC兲 method with the Inter-

national Color Consortium 共ICC兲 color management frame-

work. MacDonald and Morovic

compared several meth-

ods of gamut mapping on ﬁne art painting using La

color space. These methods are the paper cast removal,

lightness mapping, orthogonal clipping, chord clipping, and

gamut compression. For different paintings with different

percentages of out-of-gamut, different gamut mapping

methods are reported to have the best performance.

Laihanen

presented two approaches of color mapping us-

ing LABNU, a color space similar to CIELAB. These ap-

proaches are gamut compressing with constant hue and

lightness and gamut compression toward the center of light-

ness axis.

We develop the efﬁcient technique of color gamut clip-

ping for color image processing using luminance, hue, and

saturation 共LHS兲 and YIQ. RGB, luminance, and saturation

clippings are compared. Efﬁciency of the clipping tech-

niques is also investigated.

2 Color Coordinate Systems

Many three-dimensional color spaces have been proposed

and adopted in different applications in the last few de-

cades. All of them take different approaches to represent

the trichromatic nature of light to satisfy their objectives.

For example, the CIELAB and CIELUV spaces

promote

uniformity of practice. In CIELUV, if two colored lights,

and C

, are mixed additively to produce a third color

, C

lies on a straight line on a chromaticity diagram

joining C

and C

at a position that can be calculated from

the relative amounts of C

and C

The LHS color space

16,17

is derived based on the Max-

well triangle in the RGB color cube. The LHS color space

is a cylindrical coordinate system where the vertical axis

corresponds to the luminance and the horizontal plane cor-

responds to the chromatic perceptions. The hue, saturation,

and value 共HSV兲 and hue, lightness, and saturation 共HLS兲

color spaces,

which are also known as the hexcone model

and double hexcone model, respectively, are similar to the

LHS color space except that the transformations are simpli-

ﬁed. The generalized lightness, hue, and saturation 共GLHS兲

color model,

developed by Levkowitz and Herman, is a

generalization of HSL, HSV, HLS, and other special mod-

els.

The National Television Systems Committee 共NTSC兲

develops the YIQ color space for commercial color televi-

sion broadcasting and other applications. YIQ is a record-

ing of RGB for transmission efﬁciency. LHS and YIQ are

utilized here due to their efﬁciency of transformation.

2.1

LHS Color Coordinate System

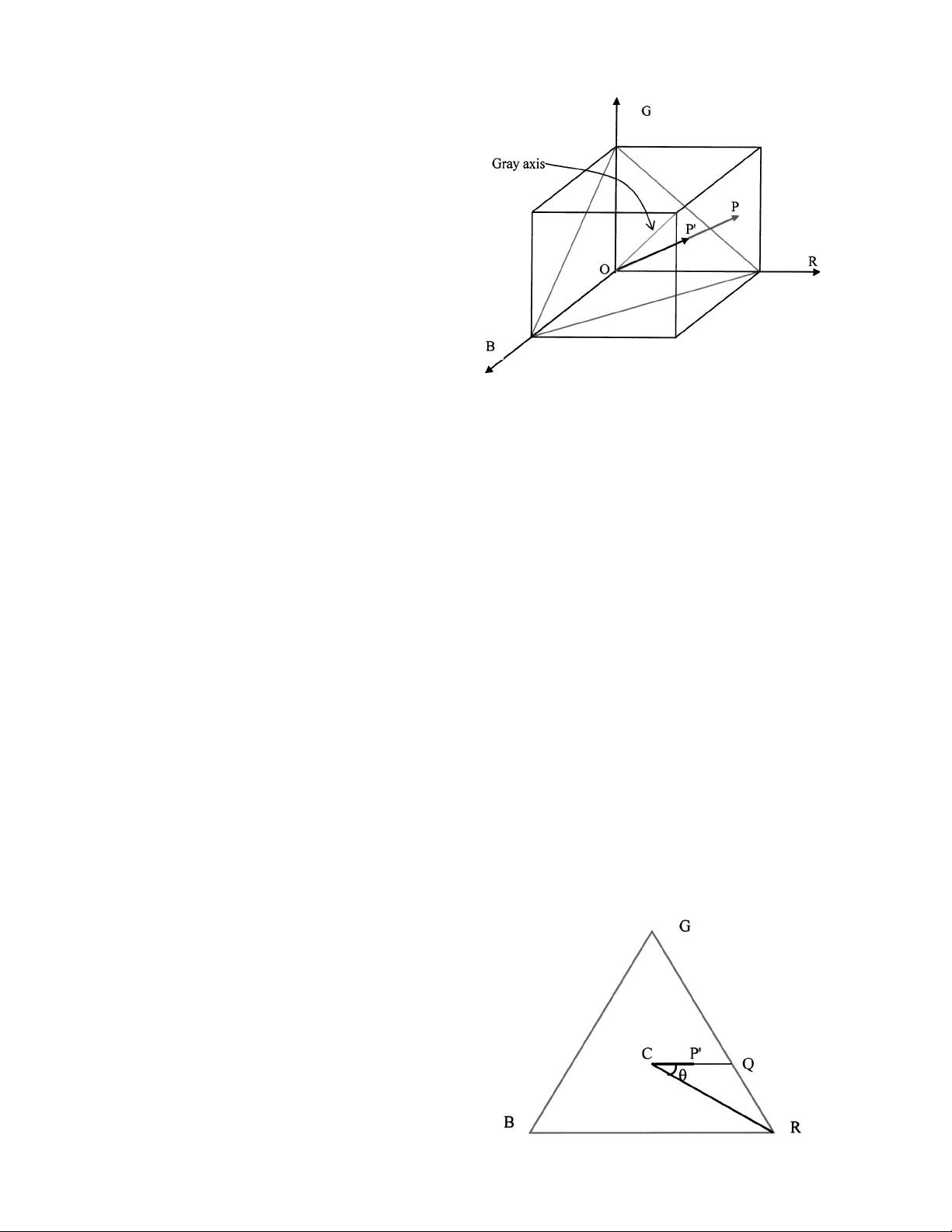
The LHS color coordinate system has three components,

luminance 共L兲, hue 共H兲, and saturation 共S兲. Its development

is based on the Maxwell triangle in the RGB color cube as

shown in Fig. 1. The corners of the Maxwell triangle are

关1,0,0兴, 关0,1,0兴, and 关0,0,1兴 in the RGB cube. Given a vec-

tor in the RGB cube, the length of the vector OP is propor-

tional to the luminance, and the intersection of the vector

OP and the Maxwell triangle represent the attributes of hue

and saturation. Given the intersection point P

⬘

on the Max-

well triangle in Fig. 2, the hue is the angle between the CP

⬘

and CR, and the saturation is the ratio of the length CP

⬘

the length CQ, where C is the center of the Maxwell tri-

angle.

2.1.1

Transformation from RGB to LHS

The transformation from the RGB color coordinate system

to the LHS color coordinate system

17,20

is as follows:

Fig. 1 Maxwell triangle in the RGB cube.

Fig. 2 The intersection point OP

⬘

in the Maxwell triangle.

Yang and Kwok: Efﬁcient gamut clipping...

702 Optical Engineering, Vol. 42 No. 3, March 2003

剩余11页未读，继续阅读

高启强668

粉丝: 3631
资源: 10

使用LHS和YIQ的高效色彩图像gamut裁剪技术

Color Gamut 色域matlab 编码

Color Gamut 色域matlab 编码 免积分

color gamut 画图软件

`BT709数据格式

slog3-s-gamut3.cine_to_s709

色温t和色域gamut的值与色坐标xylv的换算公式

显示colorspacious.rgb_to_lab源代码

写一篇关于QLED的短文并翻译成英文。

显示器色彩主要参数介绍

最新资源

Color Gamut 色域matlab 编码免积分