PSO算法解决最短路径问题详解

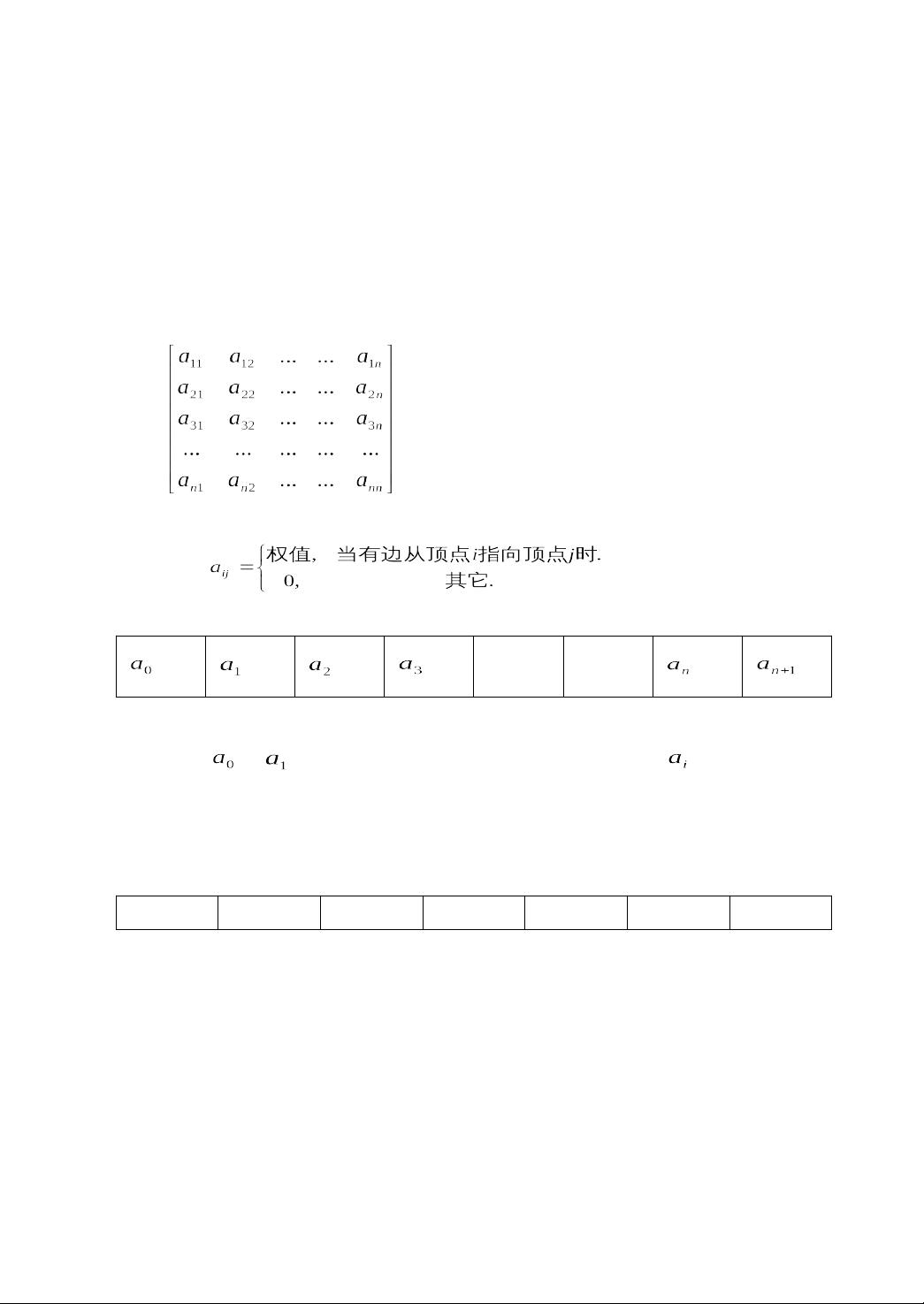
"本文档介绍了如何使用粒子群优化算法（PSO）解决最短路径问题。内容包括PSO算法中数据的表达方式、生成概率表的方法以及初始化粒子的步骤，并概述了PSO算法求解最短路径问题的模型。" 在寻找图中两点间的最短路径问题上，PSO算法是一种有效的优化方法。该算法基于群体智能，通过模拟鸟群寻找食物的过程来寻找最优解。在本案例中，PSO被应用来找出网络或图中源点到汇点的最短路径。 4.1 粒子群算法的数据表达方式： - 边的权值数据存储为矩阵形式，其中每个元素代表一对顶点之间的权重。矩阵大小为n×n，n为顶点的数量。 - 源点到汇点的最短路径存储在一个二维数组中，第一列记录每个顶点的邻接顶点数量，其余列记录邻接顶点的编号。 4.2 生成概率表： - 概率表用于确定粒子在搜索空间中移动的方向。每行对应一个顶点，列包含其邻接顶点及其对应概率。概率的计算基于边的权重的倒数，即Pi,j = Wi,j / sum_i，其中Wi,j是顶点i与其第j个邻接顶点之间边的权重，sum_i是顶点i所有邻接边权重的倒数之和。 4.3 初始化粒子： - 粒子的初始路径生成始于源点，随机生成一个0到1之间的数x，然后在概率表中找到第一个大于等于x的Pi,j，对应的邻接顶点编号被加入最短路径数组。这个过程持续进行，每次使用新顶点作为起点，直到遍历完所有顶点。 4.3 PSO算法求解最短路径问题的模型： - 解序列S由n个节点组成，每个节点代表路径上的一个顶点。模型定义了一种交换子SO，可以交换解S中的任意两个点以生成新的解。通过不断应用这种算子并更新粒子的位置，PSO算法逐步逼近最短路径。 PSO算法的核心在于粒子的个体经验和全局经验的结合，即每个粒子不仅依据自身的历史最佳位置（个人极值）更新速度，还参考群体的最佳位置（全局极值）。通过迭代，粒子群逐渐优化其路径，最终找到接近或等于最短路径的解决方案。这种方法尤其适用于处理复杂网络中的最优化问题，如交通网络中的最短路径规划。