DFT与FFT应用:信号频谱分析实验
需积分: 19 143 浏览量
更新于2024-06-29
3
收藏 2.43MB DOCX 举报
"数字信号处理仿真实验教程,主要涵盖DFT(离散傅里叶变换)和FFT(快速傅里叶变换)的应用,适用于初学者进行频谱分析。"
在数字信号处理领域,DFT(Discrete Fourier Transform)和FFT(Fast Fourier Transform)是两个至关重要的概念。DFT是将离散时间序列转换到频域的工具,而FFT则是一种高效计算DFT的方法。在这个北京理工大学的实验中,学生将通过实践深入理解这两个概念及其在信号分析中的应用。
实验的目的在于:
1. 深化对DFT基本原理的理解,这包括了解DFT如何将时域信号转化为频域表示,以及其与连续时间傅里叶变换(DTFT)的关系。DFT是DTFT在有限个等间隔频率点上的取样,这有助于分析有限长度的离散信号。
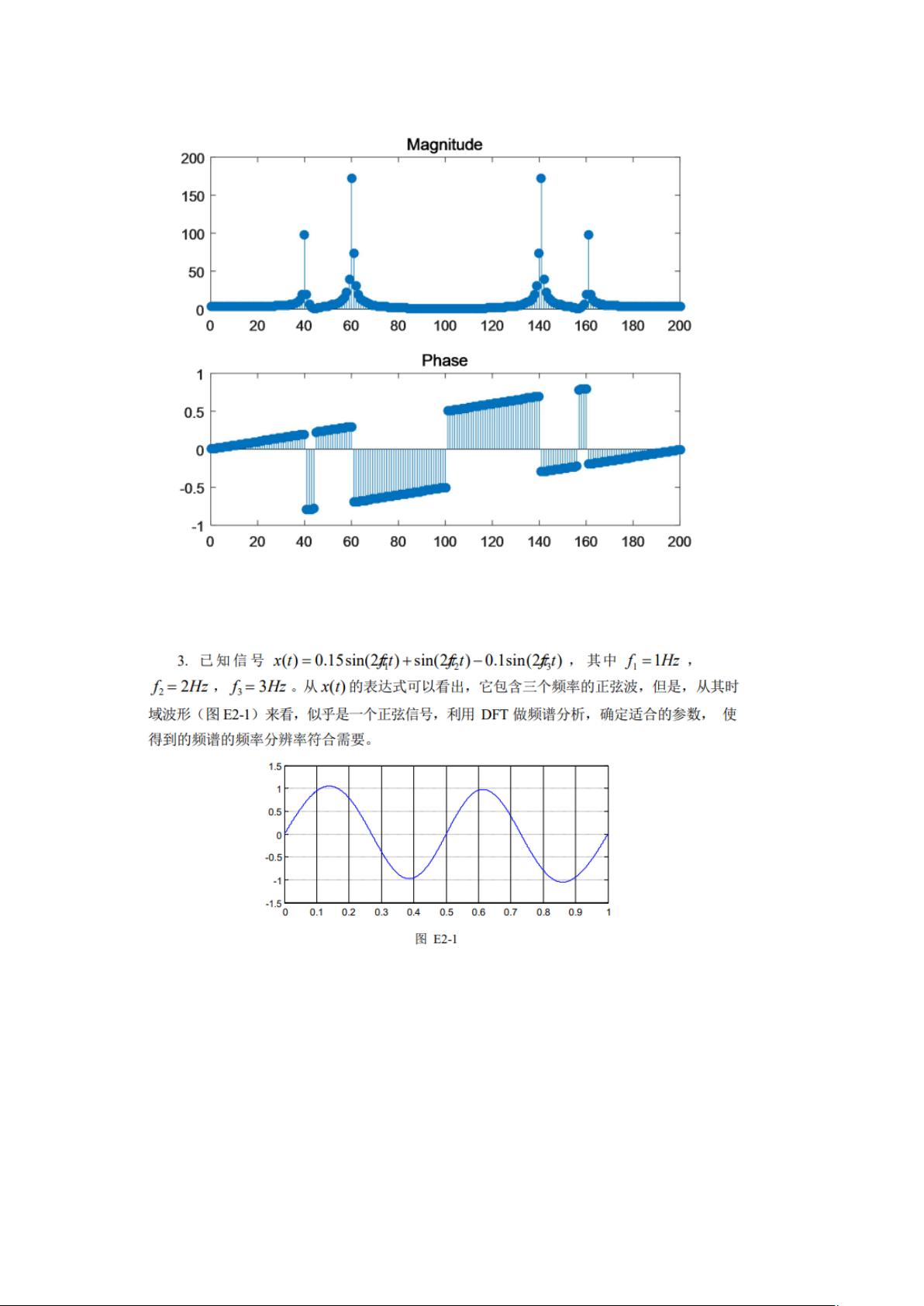
2. 应用DFT来分析信号的频谱特性,这对于识别信号的频率成分至关重要。在实验中,通过计算和可视化DFT的结果,学生可以观察信号的幅度谱和相位谱,从而揭示信号的频率组成。
3. 通过实际操作,深入理解DFT在频谱分析中的作用,以及如何利用它来解释现实世界的现象并解决问题。
实验内容分为几个部分:
(1)首先,给出了一个5点序列x,通过计算DFT并绘制幅度和相位图,展示了DFT如何反映信号的幅度和相位特性。
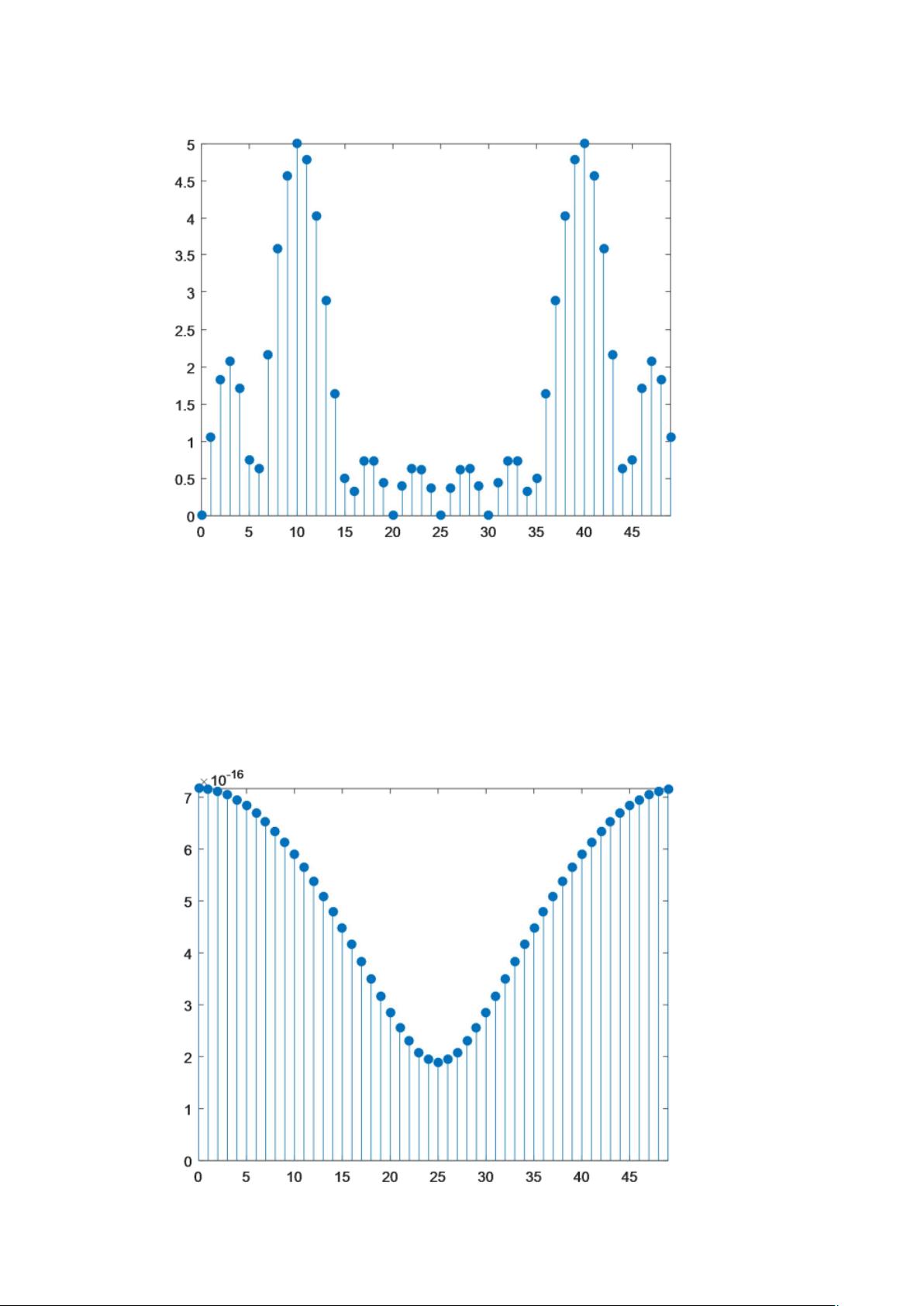
(2)然后,使用相同序列x,但这次通过FFT进行计算,并用茎图展示结果。FFT相比于DFT提高了计算效率,尤其是在处理大数据集时。
(3)进一步扩展,序列x通过添加零填充至128点,再次进行FFT计算。这样做可以提高频率分辨率,使得频谱分析更为精确。
(4)最后,通过一个包含两种正弦波的11点序列,演示了DFT如何提供DTFT的近似,当N增大时,DFT的结果更接近于DTFT。
实验通过MATLAB代码实现,学生可以在实际操作中熟悉这些概念,从而增强对数字信号处理理论的理解。通过这些实验,学生不仅能够掌握DFT和FFT的基本运算,还能学会如何利用它们来分析和解析复杂的信号结构。
2023-05-07 上传
点击了解资源详情
2023-07-07 上传
2017-04-02 上传
2024-06-25 上传
2024-05-23 上传
做题想AC
- 粉丝: 90
- 资源: 2
最新资源
- Sumo_Asteroids:我不知道我在做什么
- kafka-consumer-manager:适用于kafka消费者的包装器,支持健康检查,重试和偏移差异报告
- djangosimple:从初学者到高级使用django的项目
- ANNOgesic-1.0.17-py3-none-any.whl.zip
- Home1:1个
- refocus-collector
- ats-ebp-validator:符合 CableLabs ATS 和 EBP 规范的传输流验证软件
- Python库 | msgpack_rlp-0.6.1-cp27-cp27mu-manylinux1_i686.whl
- torch_sparse-0.6.12-cp37-cp37m-win_amd64whl.zip
- 迪马股份迪马股份2020年年度报告.rar
- TreeCracker:基于树的Minecraft种子饼干(MSCT)
- LitDatabase:C ++中的一个简单数据库
- cordova-smartlook:适用于Cordova Android的官方Smartlook SDK插件
- classic-arcade-game-clone
- doshemee:使用C ++和SMFL进行游戏编程的教程
- GuessNumGame