理解有向图的强连通分量:Kosaraju算法解析
需积分: 50 122 浏览量
更新于2024-07-20
收藏 651KB PPT 举报
本文主要介绍了有向图的强连通分量的概念以及如何利用Kosaraju算法来计算它们。
有向图的强连通分量是指在一个有向图中,如果任意两个节点都可以互相到达,那么这些节点就构成了一个强连通分量。换句话说,强连通分量是图中最大的子图,其中任意两个不同的节点都是相互可达的。如果图中的所有节点都属于同一个强连通分量,那么这个图被称为强连通图。
计算强连通分量的一种常见方法是Kosaraju算法,它包括两个主要步骤:
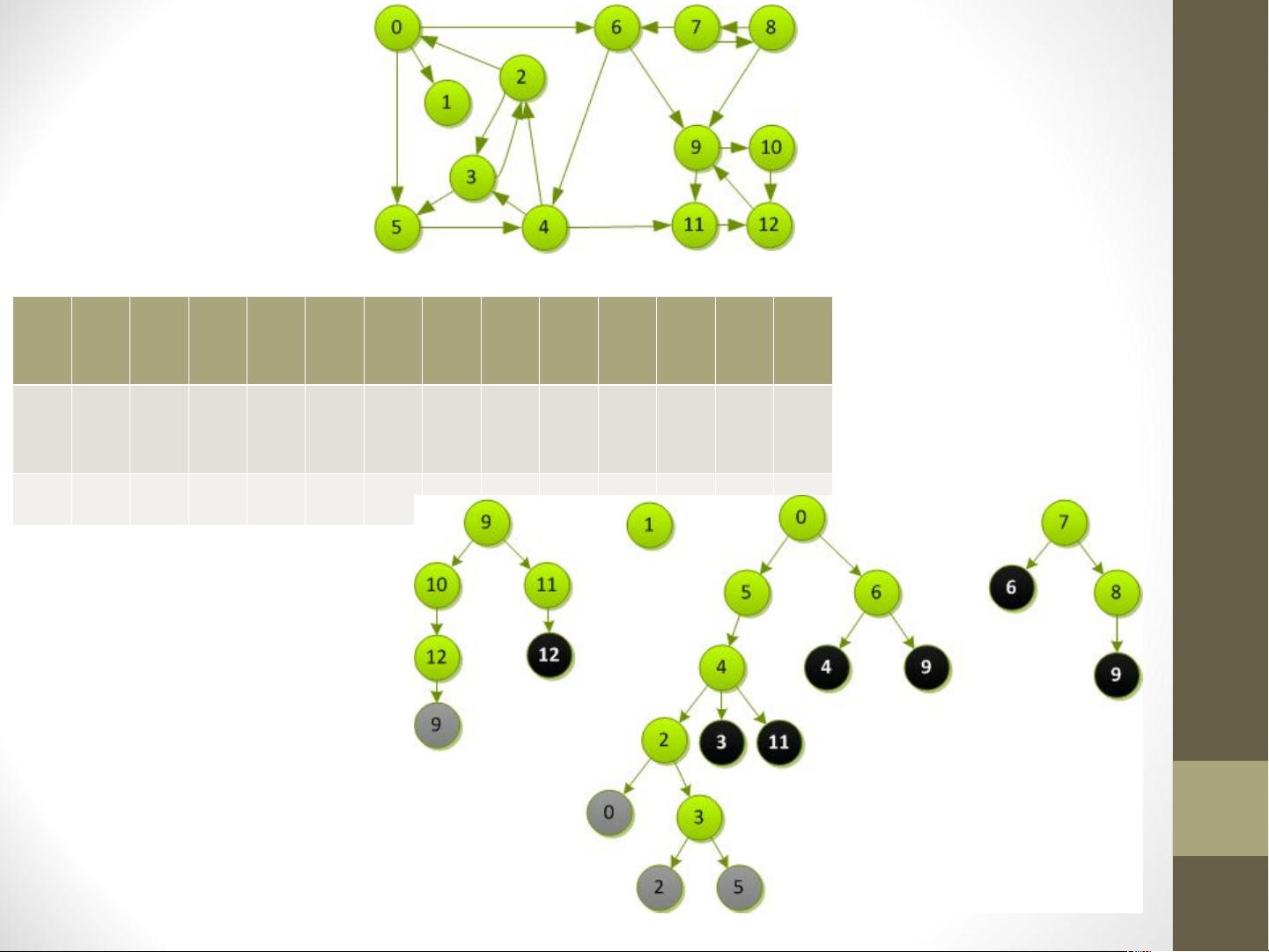
1. 首先,对原始有向图进行深度优先搜索(DFS)并记录每个节点的结束时间(f[u])。这一步是为了确定节点的拓扑排序。
2. 然后,构造图的转置GT,即所有边的方向反转。接着再次进行DFS,但这次按照结束时间f[u]递减的顺序处理未访问过的节点。每次DFS会找到一个新的强连通分量,因为按照结束时间的顺序,我们总是先访问那些可以到达当前节点的节点。
以下是一个简单的Kosaraju算法的伪代码实现:
```
Procedure Kosaraju(G):
// Step 1: DFS for original graph and calculate finishing time f[u]
for each vertex u in topological order (reverse order of finishing time)
if u is unvisited
dfs(G, u)
// Step 2: DFS for transpose graph GT
initialize all vertices as unvisited
scc = 0 // number of strong connected components
for each vertex u in order of finishing time f[u] (decreasing order)
if u is unvisited
dfs(GT, u)
scc++
Procedure dfs(G, u):
mark u as visited
for each neighbor v of u in G
if v is unvisited
dfs(G, v)
```
在这个算法中,`map[x,i]`数组用于存储与点x邻接的第i个点的编号,`map[x,0]`记录与x邻接的点的个数。`visit`数组用于标记节点是否已被遍历,`list`数组记录节点的遍历顺序,`n`和`m`分别表示图中的节点数和边数,`pos`跟踪已添加到`list`中的节点数量,而`scc`记录了找到的强连通分量的数量。
在实际应用中,Kosaraju算法可以有效地找出有向图中的所有强连通分量,这对于理解图的结构、网络分析和数据流分析等领域具有重要意义。通过深入理解这个算法,我们可以更好地处理和解决与有向图强连通性相关的问题。
410 浏览量
7396 浏览量
381 浏览量
102 浏览量
259 浏览量
135 浏览量
2024-12-24 上传
187 浏览量
167 浏览量
priority_ez
- 粉丝: 28

最新资源
- Haroopad Linux版发布:跨平台离线Markdown编辑器
- 离线安装Kubernetes 1.24.1环境教程
- Delphi7图书管理系统源码详解与应用
- NEC WriteEZ3_78K0 FLASH编程器GUI使用教程
- PHPWord库:轻松处理Word文档内容
- C#语言中的元启发式算法探究
- 深入分析VNC源码与协议细节
- Android NumberPicker实现城市与生日选择功能
- PHPUnit测试用例展示PHP操作Excel库功能
- Java项目实战:demoproject2技术解析
- LabVIEW中传统与小波去噪算法性能对比研究
- VC字符转换为十进制与十六进制教程
- Android面试题整理:从朋友处收集的精选题目
- QT编程实践:图书管理系统开发教程
- A星算法在Winform中的自动寻径功能演示
- 清华版数据结构教程精要讲义