Python实现二叉树遍历：先序、中序与后序

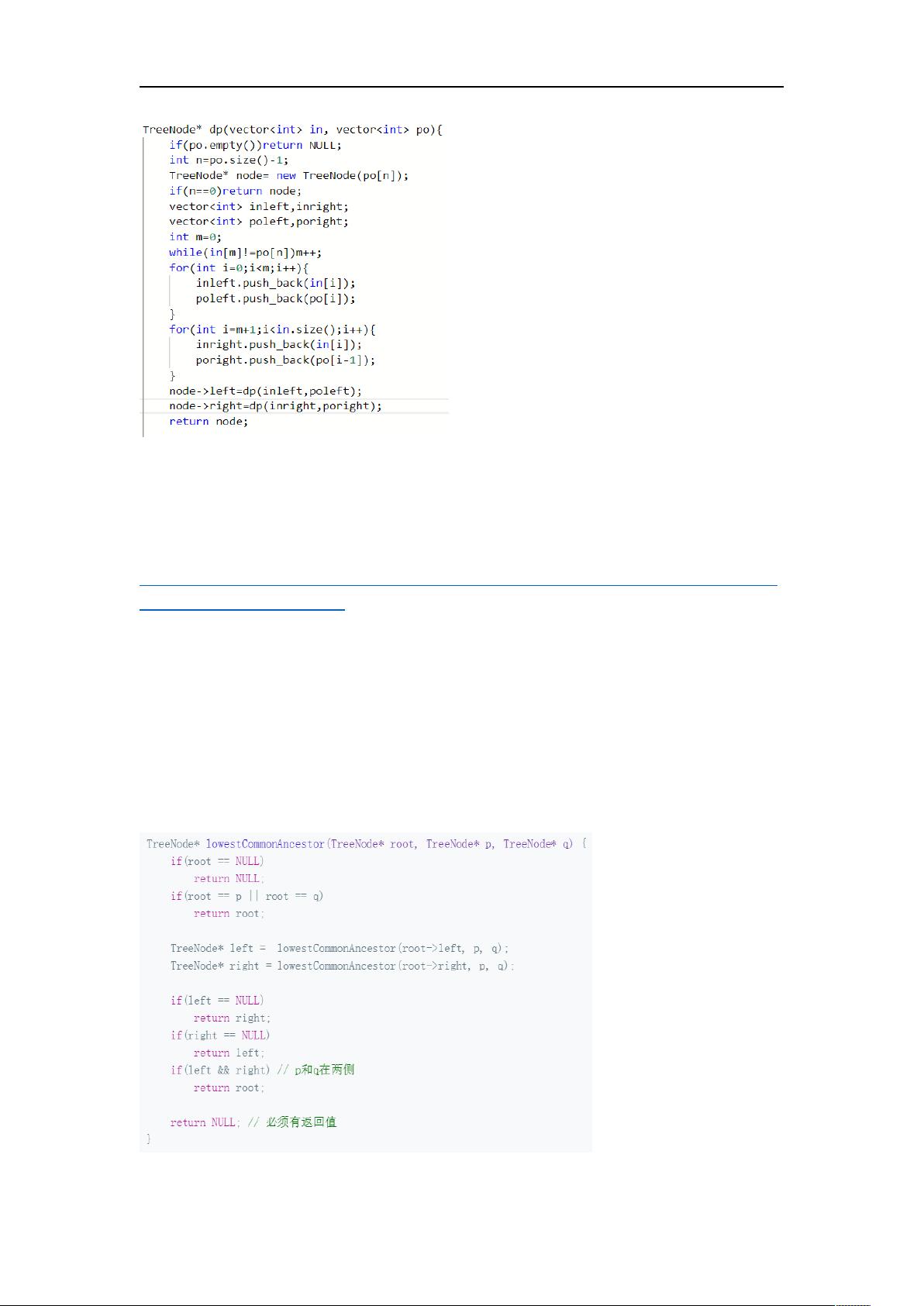
在本文档中，主要探讨了在编程中如何实现二叉树的三种基本遍历方式：先序遍历、中序遍历和后序遍历。这些遍历方法是数据结构和算法中常见的操作，对于理解二叉树的结构和处理树形数据具有重要意义。 1. **先序遍历**: 先序遍历遵循“根节点 -> 左子树 -> 右子树”的顺序。在C++代码示例中，使用栈辅助实现。首先将根节点入栈，然后进入一个循环，当栈不为空时，弹出栈顶元素，将其值添加到结果向量中，接着按照先右后左的顺序将子节点压入栈。这样可以确保在遍历完当前节点的右子树后再访问左子树。 代码片段： ``` vector<int> preorderTraversal(TreeNode* root) { vector<int> rst; if (!root) return rst; stack<TreeNode*> st; st.push(root); while (!st.empty()) { TreeNode* node = st.top(); st.pop(); rst.push_back(node->val); if (node->right) st.push(node->right); if (node->left) st.push(node->left); } return rst; } ``` 2. **中序遍历**: 中序遍历遵循“左子树 -> 根节点 -> 右子树”的顺序。实现上，先遍历左子树直到遇到叶子节点，然后访问根节点，最后遍历右子树。代码中通过两个嵌套的`while`循环来实现，外层循环负责处理剩余的左子树，内层循环则用于找到并访问当前节点。 代码片段： ``` vector<int> inorderTraversal(TreeNode* root) { vector<int> rst; if (!root) return rst; stack<TreeNode*> st; while (!st.empty() || root) { // 遍历左子树 while (root) { st.push(root); root = root->left; } // 出栈并访问根节点 root = st.top(); st.pop(); rst.push_back(root->val); root = root->right; } return rst; } ``` 3. **后序遍历**: 后序遍历遵循“左子树 -> 右子树 -> 根节点”的顺序。与前两种不同，后序遍历通常需要一个额外的辅助栈来存储节点，以实现先左后右的入栈顺序。出栈时，由于后序遍历需要的顺序是根右左，因此需要借助`reverse`函数进行反转。 代码片段： ``` vector<int> postorderTraversal(TreeNode* root) { vector<int> re; if (root == NULL) return re; stack<TreeNode*> st; st.push(root); // ... (同先序和中序的栈操作) // 后续操作：逆序输出栈中的元素 while (!st.empty()) { re.push_back(st.top()); st.pop(); } // 由于后序是左-右-根，所以需要反转re reverse(re.begin(), re.end()); return re; } ``` 通过这些代码片段，你可以理解和实现二叉树的先序、中序和后序遍历，它们在实际编程中常用于构建二叉搜索树的操作，如构建和查找树结构，或者用于构建表达式树等场景。熟练掌握这些遍历技巧有助于提高编程效率和解决问题的能力。