对比学习结构化世界模型

需积分: 10 81 浏览量更新于2024-07-09 收藏 2.27MB PDF 举报

"这篇论文是关于对比学习在构建结构化世界模型中的应用，由Thomas Kipf、Elise van der Pol和Max Welling等人在ICLR 2020会议上发表，属于计算机视觉领域的开源研究。" 正文: 《对比学习结构化世界模型》(Contrastive Learning of Structured World Models) 是一篇探讨如何从原始感官数据中学习结构化世界模型的论文。该论文主要关注的是如何模仿人类认知中对物体、关系和层次的理解，并将其应用于机器学习。作者提出了一种名为对比学习结构化世界模型（Contrastively-trained Structured World Models，简称C-SWMs）的方法。 C-SWMs的核心是采用对比学习策略来学习环境中具有组合性的结构。对比学习是一种无监督或弱监督的学习方法，它通过比较相似和不相似的样本来提升表示学习的质量。在C-SWMs中，每个状态嵌入被构造成一组对象表示及其相互关系，这些关系由图神经网络（Graph Neural Network，GNN）来建模。这使得算法能够从原始像素观测中发现并识别物体，而无需直接的监督信号作为学习过程的一部分。论文在涉及多个交互对象的环境进行实验，这些对象可以由智能体独立操纵，例如简单的Atari游戏。这种环境的复杂性和动态性为评估C-SWMs的能力提供了理想平台。通过对比学习，模型能够理解并预测对象的行为和交互，以及它们如何影响环境的整体状态。 C-SWMs的贡献在于将对比学习与图神经网络相结合，有效地捕捉了环境的结构信息。这种方法对于自主机器人、强化学习和环境建模等领域具有重要意义，因为它允许智能体从无结构的输入中抽取高级抽象，并基于这些抽象做出决策。总结来说，这篇论文为构建能理解世界复杂性的机器学习模型提供了一个新视角，即利用对比学习来揭示环境中的结构，从而推进了计算机视觉和人工智能领域的发展。通过C-SWMs，无监督学习和结构化表示学习的能力得到了增强，这对于实现更智能、更自主的系统具有深远的影响。

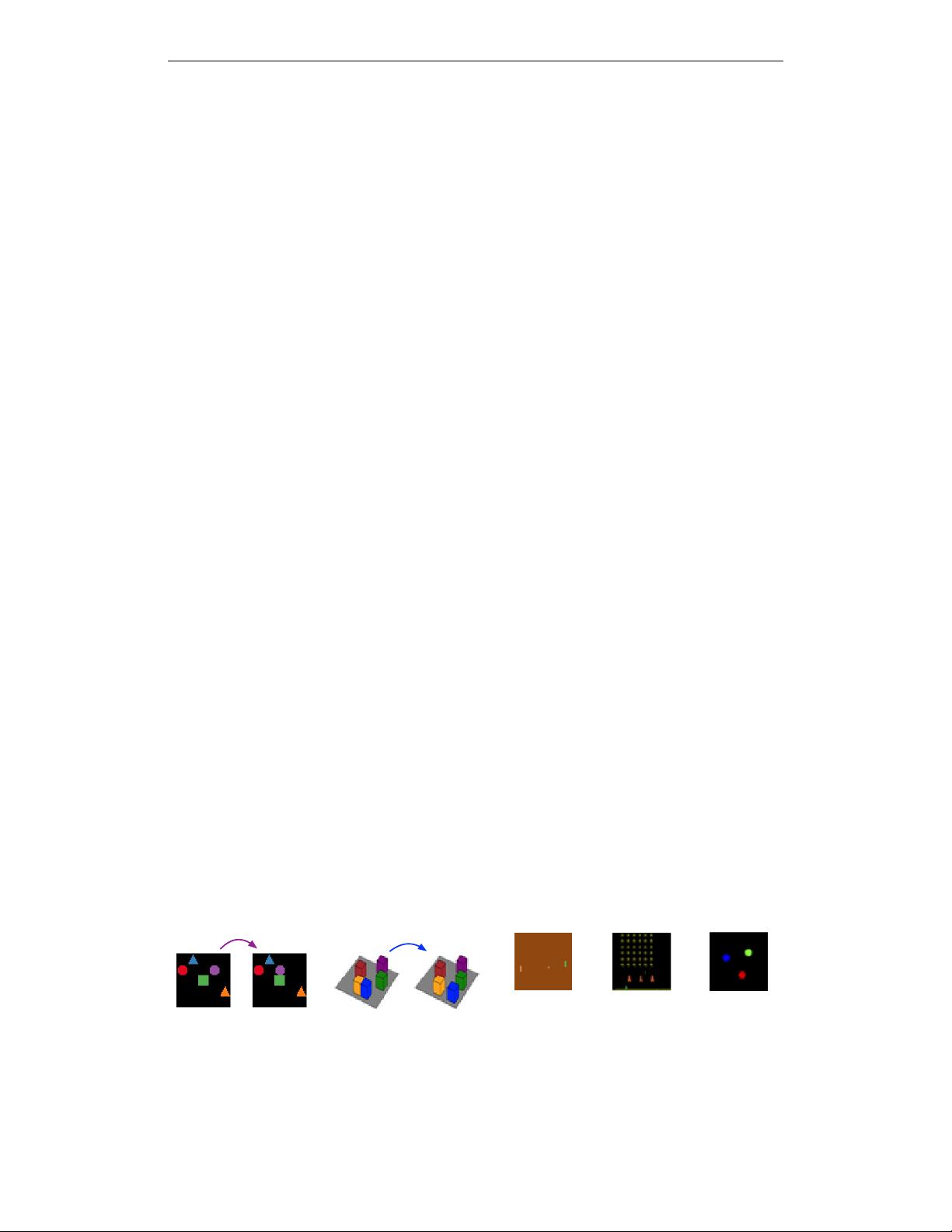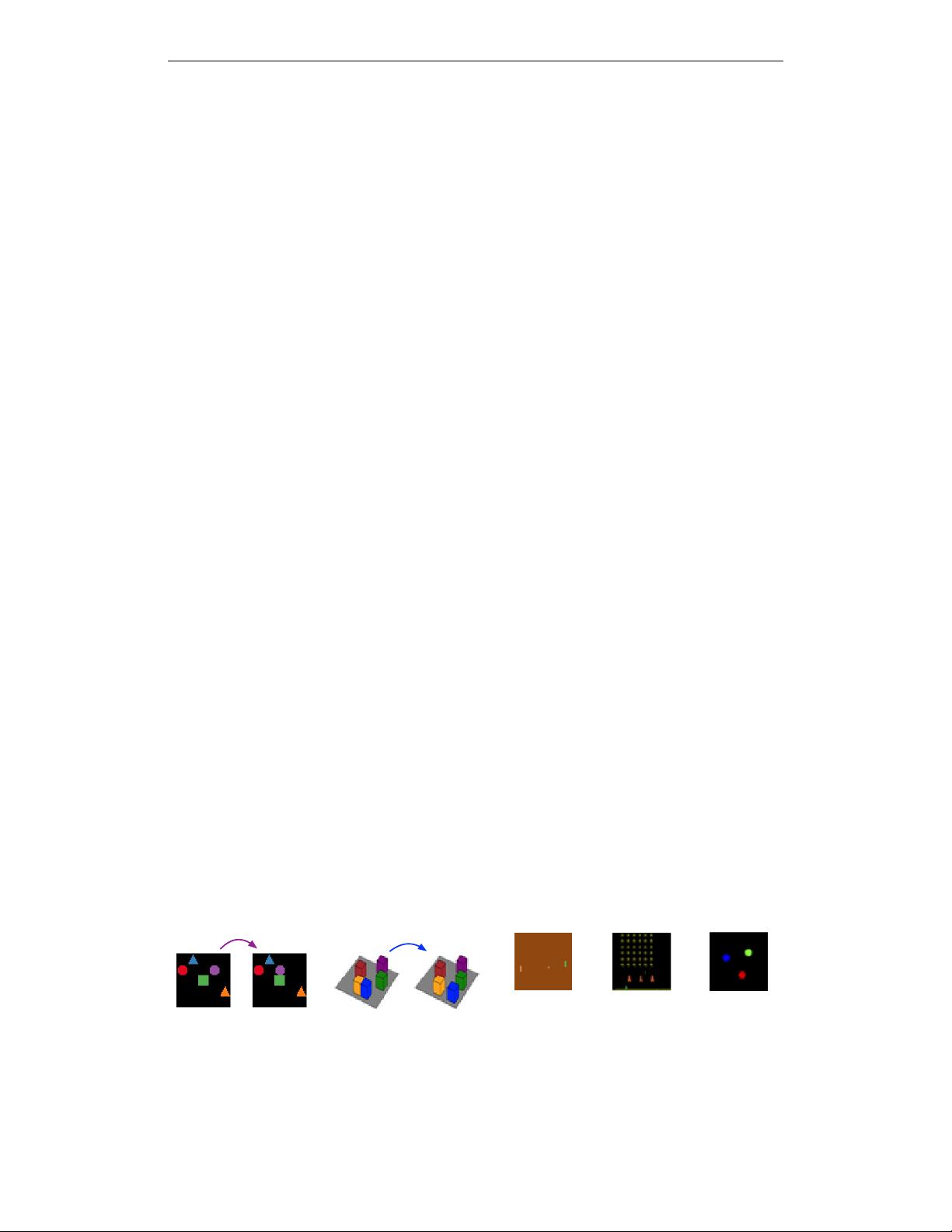
Published as a conference paper at ICLR 2020

Contrastive Learning Contrastive learning methods are widely used in the ﬁeld of graph rep-

resentation learning (Bordes et al., 2013; Perozzi et al., 2014; Grover & Leskovec, 2016; Bordes

et al., 2013; Schlichtkrull et al., 2018; Veli

ckovi

c et al., 2018), and for learning word representations

(Mnih & Teh, 2012; Mikolov et al., 2013). The main idea is to construct pairs of related data exam-

ples (positive examples, e.g., connected by an edge in a graph or co-occuring words in a sentence)

and pairs of unrelated or corrupted data examples (negative examples), and use a loss function that

scores positive and negative pairs in a different way. Most energy-based losses (LeCun et al., 2006)

are suitable for this task. Recent works (Oord et al., 2018; Hjelm et al., 2018; H

enaff et al., 2019;

Sun et al., 2019a; Anand et al., 2019) connect objectives of this kind to the principle of learning

representations by maximizing mutual information between data and learned representations, and

successfully apply these methods to image, speech, and video data.

State Representation Learning State representation learning in environments similar to ours is

often approached by models based on autoencoders (Corneil et al., 2018; Watter et al., 2015; Ha &

Schmidhuber, 2018; Hafner et al., 2019; Laversanne-Finot et al., 2018) or via adversarial learning

(Kurutach et al., 2018; Wang et al., 2019). Some recent methods learn state representations without

requiring a decoder back into pixel space. Examples include the selectivity objective in Thomas et al.

(2018), the contrastive objective in Franc¸ois-Lavet et al. (2018), the mutual information objective in

Anand et al. (2019), the distribution matching objective in Gelada et al. (2019) or using causality-

based losses and physical priors in latent space (Jonschkowski & Brock, 2015; Ehrhardt et al., 2018).

Most notably, Ehrhardt et al. (2018) propose a method to learn an object detection module and a

physics module jointly from raw video data without pixel-based losses. This approach, however,

can only track a single object at a time and requires careful balancing of multiple loss functions.

4 EXPERIMENTS

Our goal of this experimental section is to verify whether C-SWMs can 1) learn to discover object

representations from environment interactions without supervision, 2) learn an accurate transition

model in latent space, and 3) generalize to novel, unseen scenes. Our implementation is available

under https://github.com/tkipf/c-swm.

4.1 ENVIRONMENTS

We evaluate C-SWMs on two novel grid world environments (2D shapes and 3D blocks) involving

multiple interacting objects that can be manipulated independently by an agent, two Atari 2600

games (Atari Pong and Space Invaders), and a multi-object physics simulation (3-body physics).

See Figure 2 for example observations.

For all environments, we use a random policy to collect experience for both training and evaluation.

Observations are provided as 50 × 50 × 3 color images for the grid world environments and as 50 ×

50×6 tensors (two concatenated consecutive frames) for the Atari and 3-body physics environments.

Additional details on environments and dataset creation can be found in Appendix B.

Move left Move right

(a) 2D Shapes

Move left Move right

(b) 3D Blocks

Pong

(d) Space

Invaders

(e) 3-Body

Physics

Figure 2: Example observations from block pushing environments (a–b), Atari 2600 games (c–

d) and a 3-body gravitational physics simulation (e). In the grid worlds (a–b), each block can

be independently moved into the four cardinal directions unless the target position is occupied by

another block or outside of the scene. Best viewed in color.

剩余20页未读，继续阅读

潜夙

粉丝: 0
资源: 40

对比学习结构化世界模型

Article Analysis(AA): A Simple Framework for Contrastive Learning of Visual Representations

Contrastive Learning

Contextualized Spatio-Temporal Contrastive Learning with Self-S

多模态对比学习（Multimodal Contrastive Learning）的项目

基于监督对比学习的重音语音识别_Supervised Contrastive Learning for Accented Spe

contrastive-learning

ICLR2023: 时间序列对比学习自适应框架CONTRASTIVE LEARNING FOR TIME SERIES UDA

contrastive learning loss

Contrastive Learning?

attentive contrastive learning network

最新资源