方差分析在生物统计学中的应用

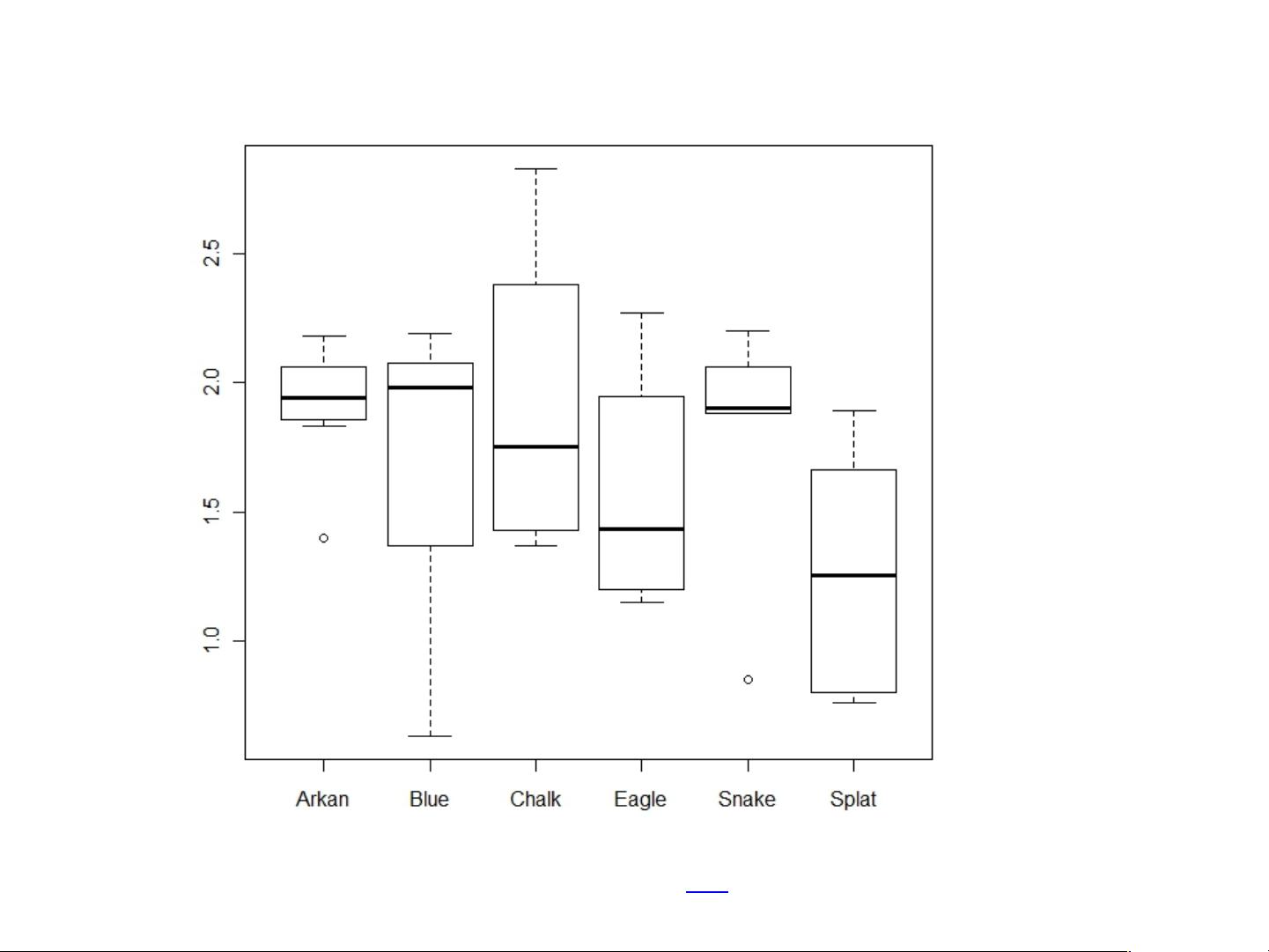
该资源是关于Biostat(生物统计学)的一次讲解，主要涉及了方差分析在生物统计中的应用，包括单向方差分析和双向方差分析，并通过一个具体的例子来阐述如何使用R进行数据分析。 单向方差分析(One-Way ANOVA)是生物统计学中一种常用的比较多个样本均值是否相等的方法。当需要比较的总体数量超过两个时，单向方差分析成为首选。它分为固定效应模型和随机效应模型： 1. 固定效应模型：在这个模型中，因子的水平被视为固定且非随机选取的。例如，在上述例子中，研究者选择的重金属污染河流的锌含量被视为固定水平。在R中，可以使用`lm()`函数来进行固定效应模型的方差分析。 ```r Call: lm(formula = DIVERSTY ~ ZINC, data = dat) ``` 这行代码表示用ZINC（锌含量）作为解释变量，DIVERSTY（物种多样性）作为响应变量进行线性回归分析。 2. 随机效应模型：在这种情况下，因子的水平被视为随机变量。在生物统计学中，这通常出现在研究设计中，如随机化区组设计或重复测量设计。 单向方差分析的基本假设包括： - 数据来自正态分布的总体。 - 各组间的方差相等，即同质性方差假设。 - 观测值在各组内是独立的。 双向方差分析(Two-Way ANOVA)用于同时考虑两个独立因素对响应变量的影响。它可以进一步分为嵌套设计和因子设计： 2.1 嵌套设计：在某些情况下，一个因素的水平被另一个因素的水平所包含，这样的设计称为嵌套设计。例如，班级内的学生可以被看作是嵌套在班级这个因素之内的。 2.2 因子设计：每个观察值都受到两个或更多独立因子的影响，每个因子有多个水平。在因子设计中，可以分析每个因子单独以及它们的交互作用对响应变量的影响。 协方差分析(Covariance Analysis)是在方差分析中考虑了协变量的情况，协变量是与响应变量相关的其他变量，可能影响实验结果。通过调整协变量，可以更好地估计因子对响应变量的真实效应。 在R中，可以使用`aov()`函数进行单向和双向方差分析，以及协方差分析。实际操作时，需要根据实验设计和数据特性选择合适的统计方法，以确保结果的有效性和可靠性。