SAMR网格上SFVE格式的逼近性和TL算法：扩散方程求解的关键策略

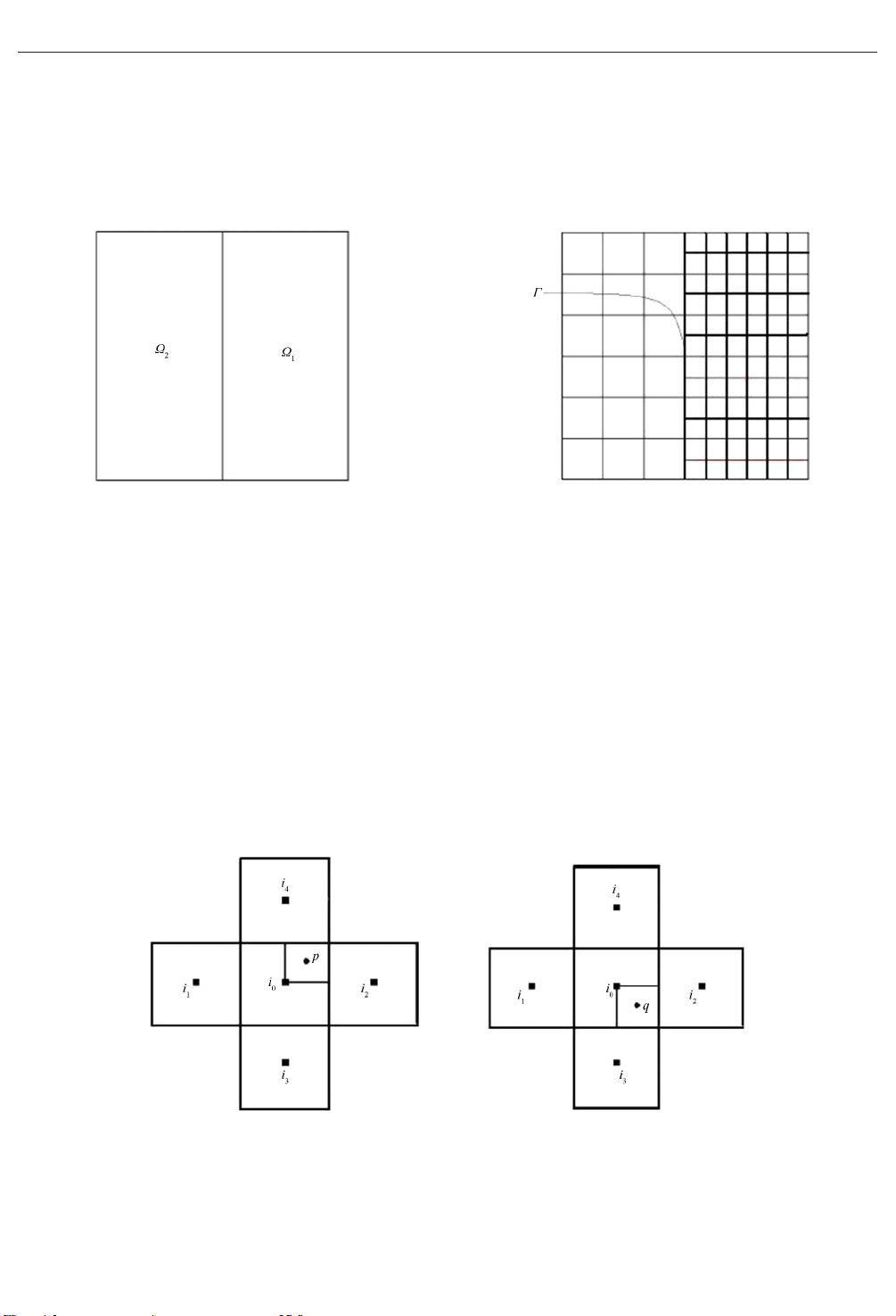
本文主要探讨了在结构自适应加密网格(SAMR)环境下，扩散方程的数值求解方法。SAMR是一种针对复杂物理现象局部区域进行网格加密的技术，特别适用于那些具有局部特征的问题，如激波、物质界面和能量传播前沿。文章首先回顾了一种常见的守恒型有限体格式，这种格式在处理扩散方程时，需要满足特定的网格加密区域条件和精细/粗化插值算子规则，以保证数值解的稳定性。 然而，为了提高逼近性和减少对网格加密区域以及插值算子的依赖，作者提出了一种新的保对称有限体元(SFVE)格式。SFVE通过在粗细界面附近添加辅助三角形单元，消除了非协调单元的存在，从而改善了网格的均匀性和精度。SFVE格式的分析结果显示，它在逼近性上优于传统格式，对网格的要求更为宽松，这有利于在SAMR网格上的实际应用。 接下来，文章的核心部分是设计并分析一种针对SFVE格式的两层网格(TL)算法。TL算法的目的是构造一个层次分明的网格结构，确保在处理网格细化和加密过程中的一致性。通过理论分析和数值实验，作者证明了该算法在SAMR网格上的收敛性，这意味着随着网格的细化，数值解将更加精确地逼近真实解。 TL算法的优势在于，它不仅可以有效地管理SAMR的复杂性，还能保持计算效率，尤其是在处理大规模网格时。通过这种方式，扩散方程在SAMR网格上的求解变得更加高效和精确，这对于许多实际工程问题的模拟具有重要意义。 总结来说，这篇文章深入研究了SAMR网格上扩散方程求解中的逼近性问题，通过对现有有限体格式的改进和两层网格算法的设计，优化了数值解的质量，为自适应网格加密技术在实际应用中的进一步发展提供了有价值的方法论支持。