MATLAB实现数值分析：误差与范数探索

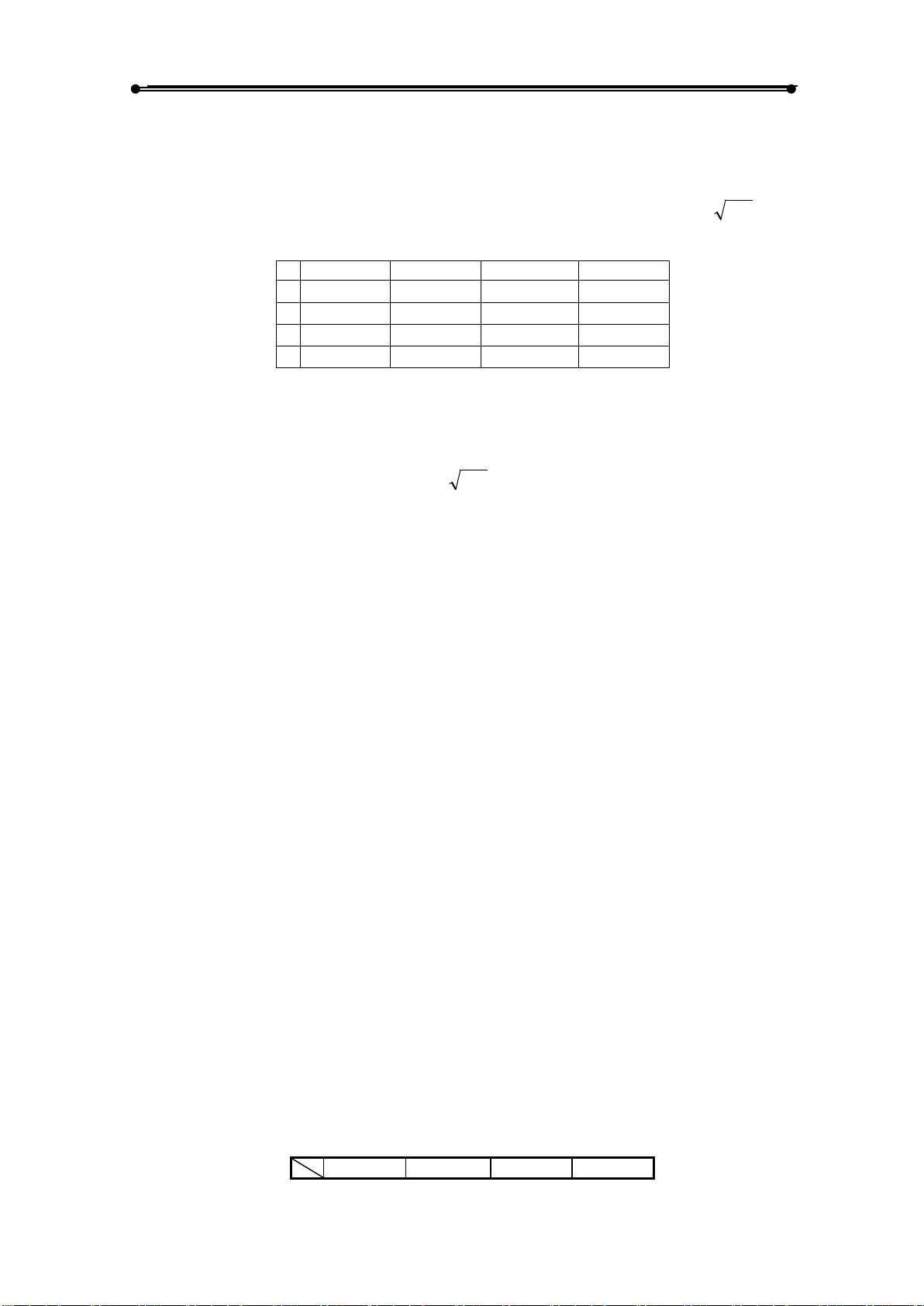
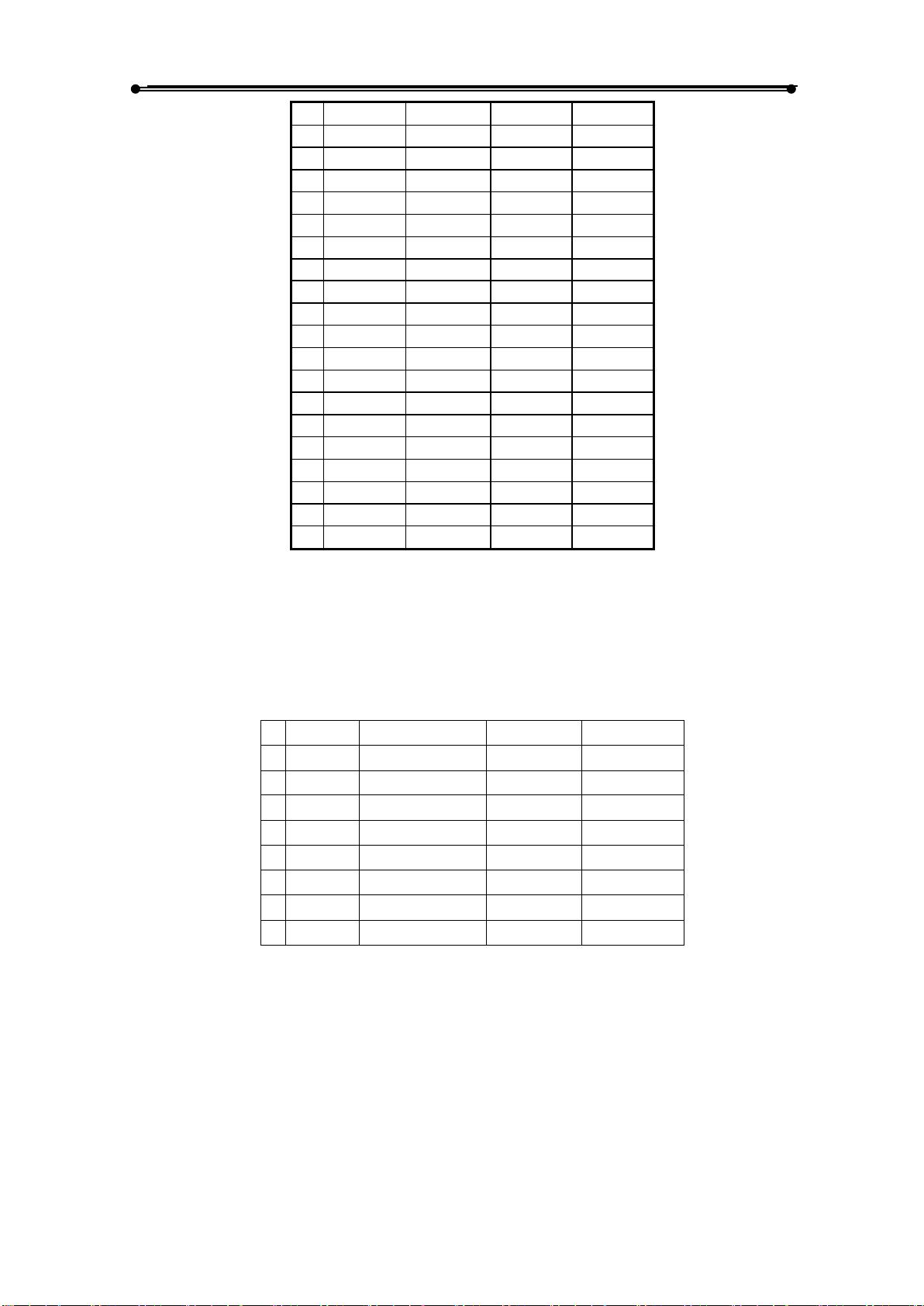
"基于Matlab的数值分析，讨论了误差与范数的概念，并通过实例展示了如何使用Matlab进行数值计算，包括求导、解线性方程组和近似值的计算。" 在数值分析中，Matlab是一个强大的工具，用于实现各种数学算法和计算。本资料主要关注误差和范数这两个核心概念，并通过实际编程示例来阐述它们在数值计算中的应用。 1. 误差的来源与处理 误差在数值计算中是不可避免的，它可能源于数据采集、近似方法以及计算过程中的舍入误差。例如，在例1.1.1中，通过差商法求导会引入误差。当使用不同的步长h来计算导数的近似值时，结果的精度会有所不同。在Matlab中，我们可以通过改变h的值来观察误差的影响。例子显示，过小的步长可能导致较大的相对误差，这是因为浮点运算的限制，而不是更小的步长总是带来更精确的结果。 2. 解线性方程组 在例1.1.2中，展示了如何使用Matlab的 `\` 运算符来求解线性方程组。对于方程组 AX = b，Matlab的 `\` 运算符可以快速找到解X。在这个例子中，我们看到对于不同系数矩阵A和向量b，Matlab都能有效地求解。对于对角占优或病态的矩阵，选择合适的求解策略是至关重要的，因为这会影响解的稳定性和计算效率。 3. 数值积分与近似 例1.1.3探讨了使用泰勒级数逼近复杂函数，如自然对数的底e。由于泰勒级数是无穷级数，计算机不能直接求和，因此需要取有限项进行近似计算。在Matlab中，可以编写循环或利用内置函数（如`sympy`库）来实现级数展开并估算误差。 通过这些实例，我们可以了解到在数值分析中，理解误差来源和控制误差的方法是非常重要的。Matlab提供了丰富的工具和函数，使得数值计算变得直观且高效。然而，使用时需谨慎，因为不恰当的参数设置可能会导致不准确的结果。同时，掌握如何评估和减少误差是数值计算中的关键技能。在实际操作中，我们需要不断调整计算参数，以达到所需的精度和稳定性。