离散信源与马尔科夫信源解析
需积分: 25 164 浏览量
更新于2024-07-27
收藏 3.18MB PDF 举报
"离散信源,马尔科夫信源,信息量,无记忆信源,离散平稳信源,信源模型,随机变量,随机矢量"
马尔科夫信源是离散有记忆信源的一个特殊类型,在信息论中具有重要地位。离散信源指的是信源输出的消息集合是有限或可数的,并且每次只产生一个单一的消息。这种信源可以被数学化地建模为随机变量,通过定义每个消息发生的概率来描述其统计特性。
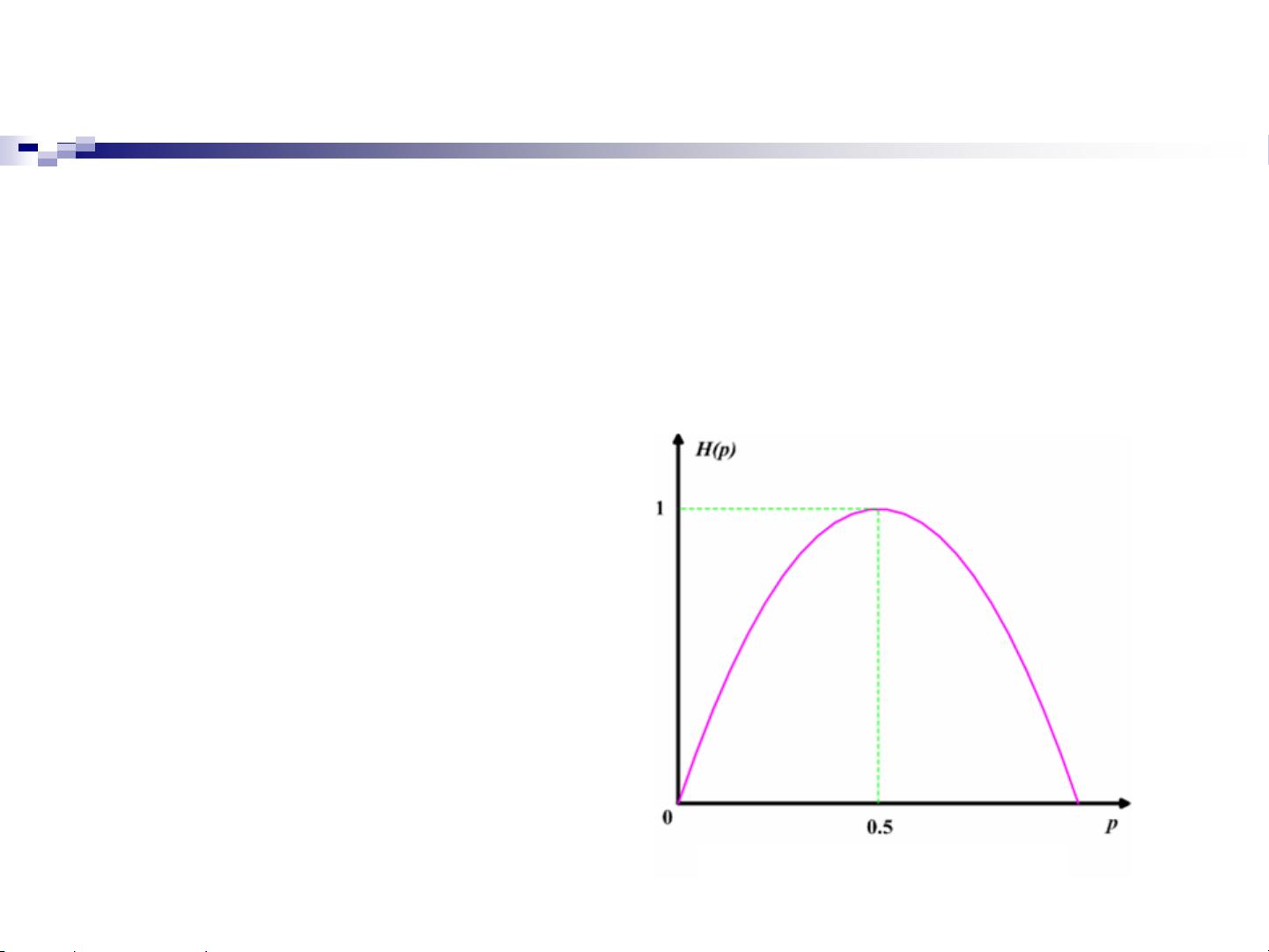
在信息论中,我们关注的是信源输出中的信息含量。信息量通常与消息的不确定性相关,一个事件发生的概率越小,它所携带的信息量越大。例如,如果扔一枚公平的骰子,每个面朝上的概率相等,那么每种结果都含有相同的信息量,因为它们的概率都是1/6。相反,如果某个结果非常罕见,它的信息量就更大。
信源的数学模型主要包括随机变量和随机矢量两种。对于离散型信源,我们使用随机变量来表示,其中每个可能的消息对应于随机变量的一个取值,其概率分布反映了信源的统计特性。如果消息的取值是连续的,我们会使用连续随机变量描述,其概率密度函数定义了每个值出现的可能性。
随机矢量则用于描述由多个符号组成的复合消息,例如,连续时间的音频信号或空间上连续的图像。这些信源的输出可以看作是在时间或空间上的序列,每个时间点或像素位置对应着一个随机变量。
马尔科夫信源是一种具有记忆的离散信源,其特点在于当前输出的状态只依赖于前几个状态,而不是整个历史。这种特性可以用马尔科夫链来建模,其中每个状态转移的概率仅取决于前一状态,而不受更早状态的影响。马尔科夫信源在文本生成、语音识别等领域有广泛应用,因为它能简洁地描述序列数据的动态特性。
除了马尔科夫信源,还有无记忆信源和离散平稳信源。无记忆信源是指下一个符号的出现不依赖于之前符号的出现,如独立同分布的随机变量序列。离散平稳信源则是其统计特性(如符号出现的概率)随时间不变的信源,这在处理大量时间序列数据时十分有用。
理解和建模不同类型的信源对于设计高效的信息传输系统至关重要,包括无失真编码、有噪信道编码以及限失真编码等。这些理论和方法不仅应用于通信工程,也在数据压缩、图像处理、自然语言处理等多个领域发挥着关键作用。
3435 浏览量
338 浏览量
201 浏览量
828 浏览量
154 浏览量
irinisha
- 粉丝: 0
- 资源: 1
最新资源
- attention
- worker-manager:您是否希望执行长时间运行的任务而又不会阻塞您的主要流程?
- ipmail-开源
- URP Shadow Receicer Shader
- systemjs-mocha-spike:SystemJS Mocha Spike
- 兄弟姐妹重布线:波哥大大学(Proyecto de la lagogo)毕业于JoséManuelGalán和Virginia Ahedo。 铝制耐火材料生产商协会,墨西哥铝业联合公司
- pity-calc:找出Genshin Impact可惜的计算器
- watershed.zip
- Memo-code-snippets-and-notes:杂项代码段和注释
- springboot075基于SpringBoot的电影评论网站系统(开题报告+论文)
- TogglWeekByTag:用于按标签进行 Toggl 每周报告的 Chrome 扩展
- C#快速学习笔记.rar
- proyecto_m17
- poc-bradesco:我旁边的Pruebas de aplicacion
- 保险行业培训资料:少儿险主打产品介绍
- 项目案例-班级管理系统