Y. Yang et al. / Information Fusion 30 (2016) 91–102 93
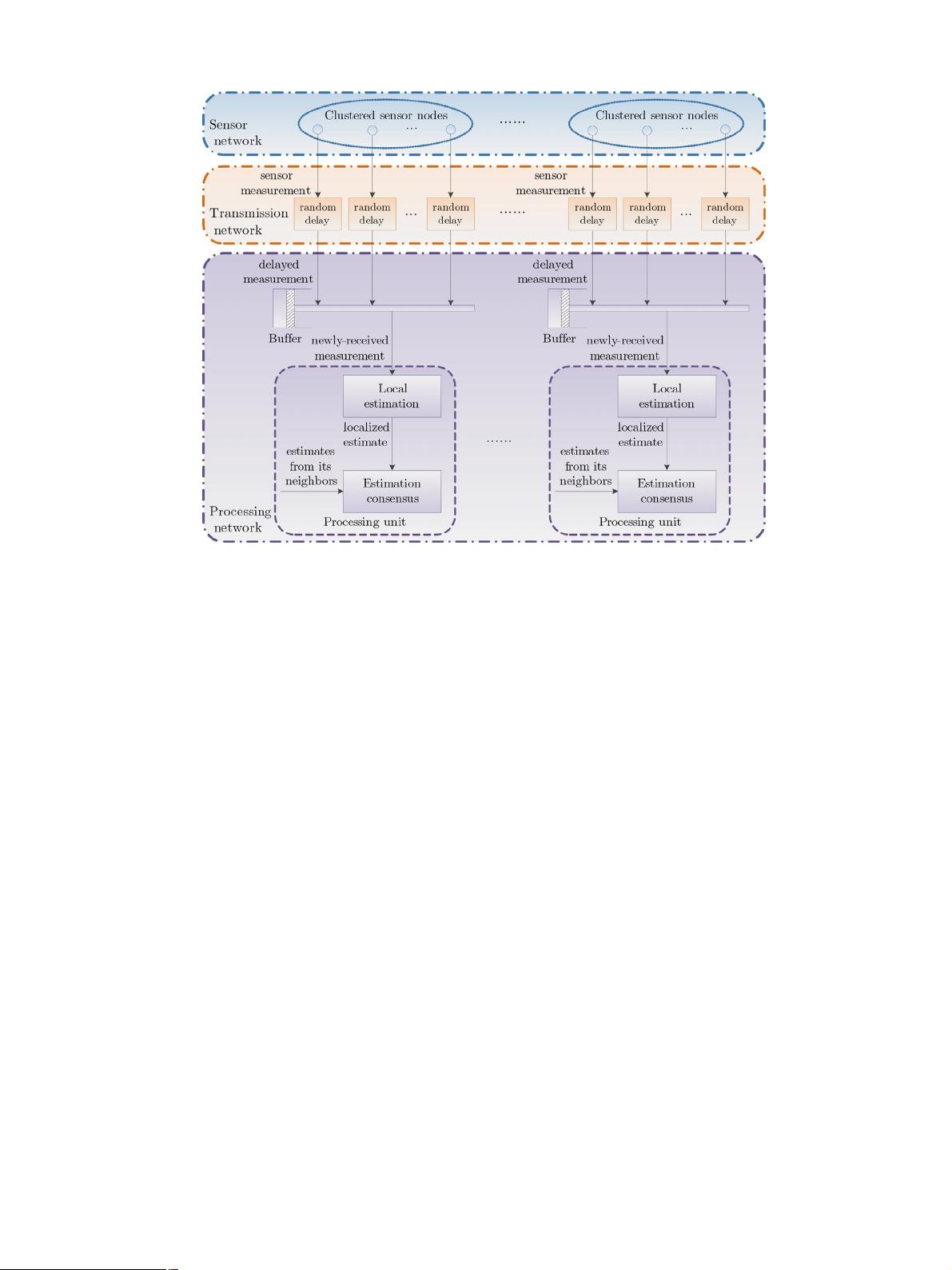
Fig. 1. Problem formulation.
is given:
min(k+1,s
m
)
j=0
γ
m
j,k+1
= 1. (5)
Moreover,
γ
m
j,k+1
is uncorrelated with x
0
, w
k
and v
k
in the corre-
sponding sensor node.
Remark 1. It is easily testified that our proposed system (1)-(5)
in a PU can be degraded to the nonlinear system without de-
layed measurements if P
{γ
m
0,k
= 1} = 1andP{γ
m
j,k
= 1} = 0for j =
1, ··· , min
(k, s
m
). Moreover, the proposed system without mea-
surement delay is also a common nonlinear system in networked
sensors. On the other hand, our system in the mth PU will be de-
graded to the nonlinear system with randomly Bernoulli delayed
measurements if
γ
m
i,k
and γ
m
j,t
are mutually uncorrelated for any k
= t, due to that the Bernoulli process is only a special case for this
Markov process [28]. Furthermore, it is equivalent to the model
in [22,23] with P
{γ
m
j,k
= 1} = 0forj = 2, ··· , min(k, s
m
), or to the
model in [25] for j = 3, ··· , min
(k, s
m
).
Except for the decentralized and distributed structure of pro-
cessing network, model nonlinearity, stochastic parameters and
mode uncertainty caused by random delay coexist in the consid-
ered system. Thus, the filter to be designed should own not only
the decentralized structure, but also the ability for joint state esti-
mation and parameter identification in the nonlinear case. Based
on it, the GCF is proposed in the following section to pursue a
tradeoff between estimation accuracy and computation cost. It is
expected to obtain not only a novel and generalized GAF for non-
linear systems with randomly delayed measurements in a single
PU, but also a scalable and distributed fusion among multiple PUs.
Remark 2. The GAF is a convenient and widely used filter in non-
linear cases [14,23]. The Gaussian density belongs to the expo-
nential family and will still be Gaussian after any linear trans-
formation. This makes the recursive operation being available and
the corresponding GAF is analytical, under reasonable Gaussian as-
sumptions. Therefore, in the considered problem, it is rational to
design a novel GAF considering random delay in the single PU to
obtain an accuracy estimate performance. Meanwhile, due to the
existence of random delay, the posterior probability of delay is also
identified.
Remark 3. Based on the novel GAF in a single PU, the following
three considerations prompt us to give the following decentralized
structure. Firstly, the decentralized structure is needed in mas-
sive data processing, which can support the multi-core processing
or cooperative processing of multiple distributed computing units.
Secondly, the computation efficiency is expected to be greatly
improved because the consensus strategy avoids computation-
intensive cross-covariance calculations among local estimate errors
in distributed fusion [29–32]. Thirdly, PUs are always geographic
proximity and have high-speed data exchange links, which can
support information interaction of consensus iteration.
3. Gaussian-consensus filter for nonlinear systems with
randomly delayed measurements in sensor networks
In this part, we will firstly derive the GEDPF for nonlinear sys-
tems with randomly delayed measurements in a PU, and then the
GCF will be presented based on the GEDPF to obtain an asymptot-
ically consistent estimate in the whole processing network.
3.1. Gaussian approximated filter in a single processing unit
In this subsection, we will derive the local estimation in the
mth PU. For simplicity, the superscript “m” is omitted without con-
fusion here, for example,
λ
m
ij,k+1
is simplified as λ
ij,k+1
.
Denote the obtained measurement sequence
{y
1
, ··· , y
l
} as Y
1: l
.
Define
ˆ℘
k|l
:= E(℘
k
|Y
1:l
), P
℘
k,t
|l
:= cov(℘
k
,
t
|Y
1:l
) = E( ˜℘
k|l
˜
t|l
),









