78 CHINESE OPTICS LETTERS / Vol. 7, No. 1 / January 10, 2009
Effect of mutual inductance coupling on superconducting
flux qubit decoherence
Yanyan Jiang (
ÿÿÿÿÿÿ
)
1,3
, Hualan Xu (
MMM
uuu
===
)
1
, and Yinghua Ji (
℄℄℄
===
uuu
)
1,2∗
1
College of Physics and Communication Electronics, Jiangxi Normal University, Nanchang 330022
2
Key Laboratory of Optoelectronic and Telecommunication of Jiangxi, Nanchang 330022
3
Department of Physics, Anqing Teachers College, Anqing 246011
∗
E-mail: jyh2006@jxnu.edu.cn
Received March 21, 2008
In the Born-Markov approximation and two-level approximation, and using the Bloch-Red field equation,
the decoherence property of superconducting quantum circuit with a flux qubit is investigated. The
influence on decoherence of the mutual inductance coupling between the circuit components is complicated.
The mutual inductance coupling between different loops will decrease the decoherence time. However, the
mutual inductance coupling of the same loop, in a certain interval, will increase the decoherence time.
Therefore, we can control the decoherence time by changing t he mutual inductance parameters such as
the strength and direction of coupling.
OCIS codes: 270.0270, 000.6800.
doi: 10.3788/COL20090701.0078.
In the quest for practica l systems for carrying out quan-
tum computations, solid-state systems that make use
of the Josephson effect are available candidates
[1,2]
.
Presently, three prototypes of superconducting qubits
are studied experimentally
[3−6]
. The interaction be-
tween quantum system and environment will cause two
demolishment processes, i.e., quantum dissipation and
quantum decohere nce
[7,8]
. The former will cause en-
ergy dissipation, a nd the latter will make the system
degenerate from coherent state to classical state
[9,10]
.
Compared with other qubit candidates (such as trapped
ions, nuclear spins, and cavity quantum electrodynamics
(QED)), decoherence presents a much more formidable
challenge to superconducting qubits. For a true two-
level qubit, decoherence occurs due to the coupling of
the qubit to its environment. However, all of the pro-
posed superco nducting q ubits have multiple energy lev-
els which result in adverse effects on quantum gate op-
erations. In fact, coupling between the computational
bases, i.e., |0i, |1i and states |n ≥ 2i of the noncomputa-
tional subspace results in significant errors for one-qubit
gate operations. Previous theoretical works on decoher-
ence of superconducting qubits have typically relied on
the widely used spin- boson model which postulates a
purely two-level dynamics, therefore neglecting leakag e
effects
[11]
. As a basic model describing a quantum sys-
tem, the spin-boson model provides a s imple and effective
way to study the q uantum dissipation characteris tics.
Based on this model, the evolution of the quantum sys-
tems is describe d as a two-level dynamics proces s. Com-
bining network graph theory with the Caldeira-Leggett
model fo r dissipative elements, Burkard, Koch, and Di-
Vincenzo (BKD) presented a multi-level qua ntum circuit
theory o f decoherence for a general circuit realization of
a superconducting qubit
[12,13]
. The decoherence of “IBM
qubit” was studied using the c ircuit theory. A number of
decoherence mechanisms can be important, being both
intrinsic characteristic to the Josephson junctions, and
current and voltage from the external control circuits.
The effect of the current or voltage fluctuations are re-
lated to the mutual inductance between external circuits
and environment. In this letter, we study the effect of
the mutual inductance between IBM qubit a nd environ-
ment for decoherence.
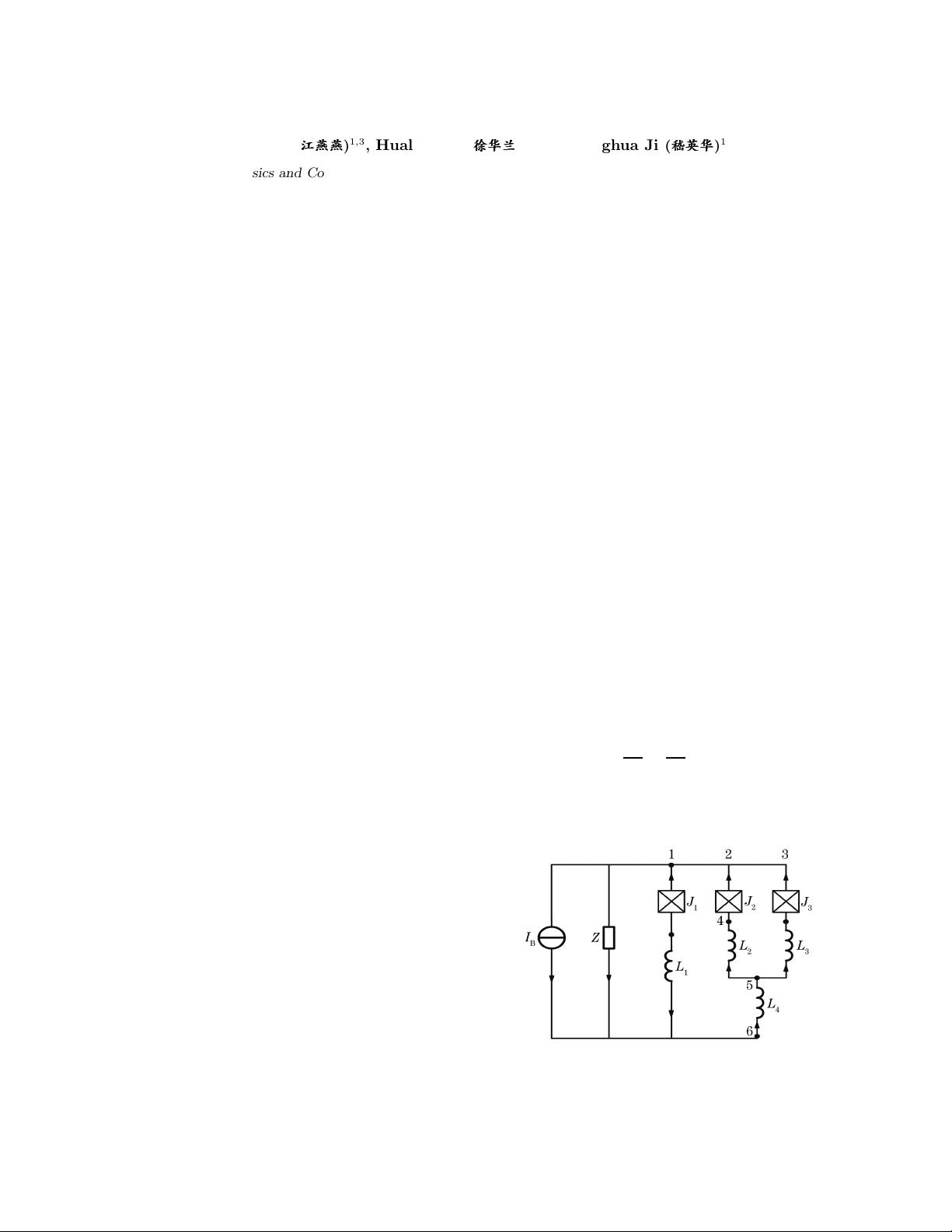
The IBM qubit is described by the electrical circuit
shown in Fig. 1. We will investigate the decoherence
property o f superconducting flux qubits coupling with
the environment. In the circuit, shunt resistors R, exter-
nal impedances Z(ω), and bias current sources I
B
form
the environment.
The constraint relation between the current flowing
through Josephson junction and voltage (flux) is
I
J
= I
C
sin ϕ, (1)
dϕ
dt
=
Φ
0
2π
V
J
(t), (2)
where, I
J
is the super-current of Josephson junction,
I
C
is the critical current of the junction, ϕ is the pulse
difference across the junction, V
J
is the voltage across
Fig. 1. Quantum circuit with flux qubit. Impedance Z
reflects the dissipative effect of environmental electromag-
netic fluctu ation on qubit. The coefficient of th e mutual in-
ductance between L
1
and L
2
, L
3
and L
4
is M
1
, while that
between L
3
and L
2
, L
1
and L
4
is M
2
. J
i
(i = 1, 2, 3): Joseph-
son junctions.
1671-7694/2009/010078-04
c
2009 Chinese Optics Letters









