MATLAB信号系统实验：绘制连续信号波形与复信号分析

本篇文档是关于MATLAB信号与系统仿真实验的报告，针对信号与系统课程，通过MATLAB编程实现了一系列实验内容，旨在帮助学生熟悉MATLAB软件的应用，并深入理解信号和系统的概念。实验分为两个主要部分，第一个部分涉及连续信号的波形图绘制，包括正弦函数（cos）、单位阶跃函数（U）、延迟单位阶跃函数（t(u(t)-u(t-1))) 和周期函数（t(u(t)-u(t-1))）的图形表示。 在实验的第2章中，具体步骤如下： 1. 用MATLAB命令画出`k`倍的余弦信号（`k*cos(w*t+phi)`），其参数分别为振幅`k=2`，角频率`w=3`，相位`phi=pi/4`。波形图显示了信号在时间`t`从0到5的周期变化，范围设定为[0,4]轴限，标题为'cos'。 2. 画出了一个线性衰减的阶跃函数`ft=(a-exp(b*t)).*(t>=0)`，其中`a=2`，`b=-1`。该函数只在`t>=0`时有效，展示了不同时间点上的函数值，范围[-1,4]，标题为'U'。 3. 实现了`t(u(t)-u(t-1))`函数，即单位阶跃函数与延迟单位阶跃函数的乘积，展示时间变量`t`的变化对输出的影响，同样在[-1,4]范围内，标题为't(u(t)-u(t-1))'。 4. 对于周期性函数`ft=(1+cos(pi*t)).*((t>=0)-((t-2)>=0))`，同样绘制了波形图，并分析其特性。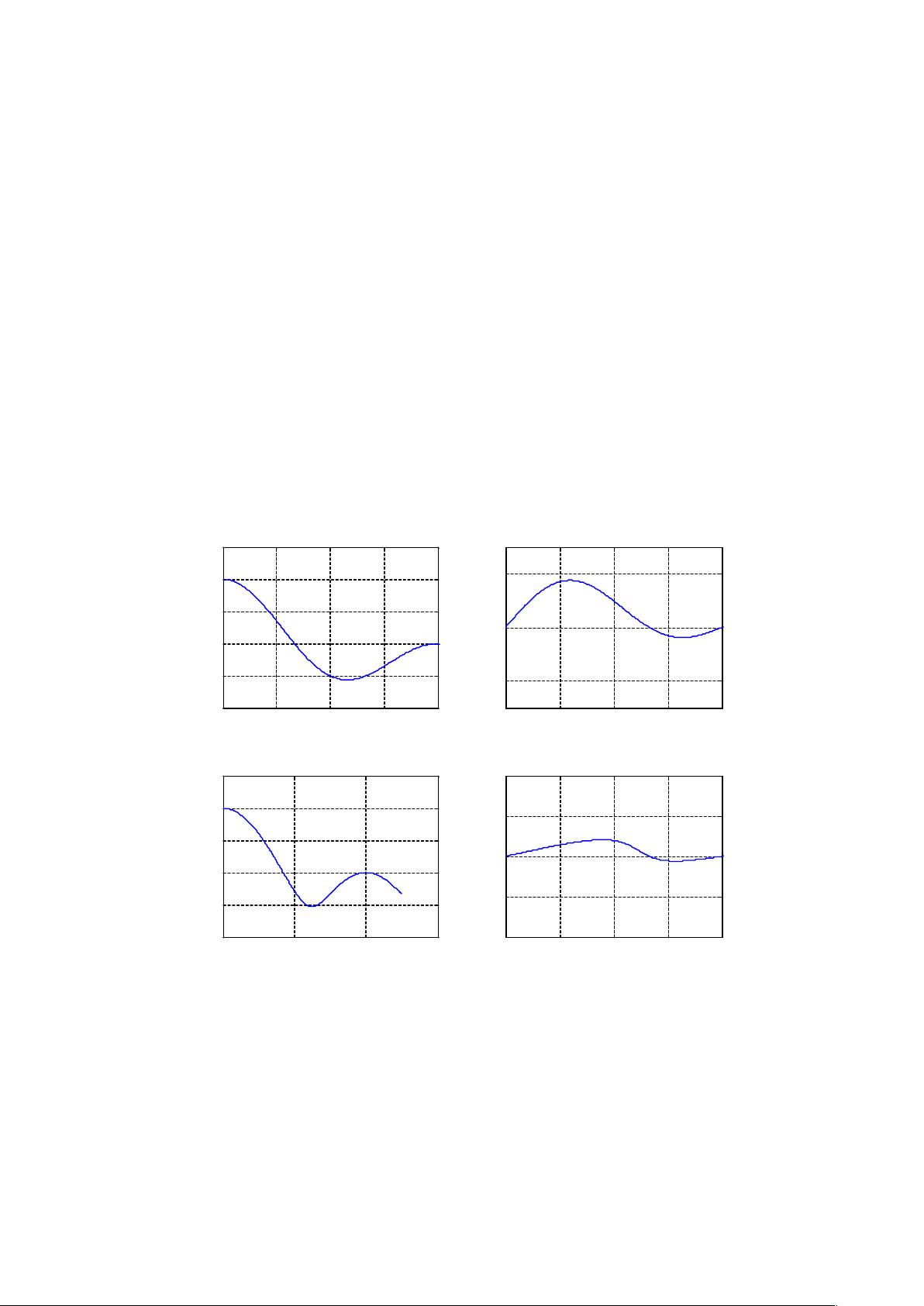 第二部分则关注复信号的分析，通过以下两个例子来处理： 1. 定义复信号`ft=a+exp((i*b)*t)+exp((c*i)*t)`，其中`a=2`，`b=pi/4`，`c=pi/2`。分别计算并绘制了实部、虚部、模（幅度）和幅角随时间`t`的变化，每个子图都设置了适当的轴限和标题，便于观察信号的属性。 2. 第二个复信号的定义和分析与第一个类似，只是参数不同。通过`subplot`函数将四个子图组织在同一图中，方便对比分析。 这些实验内容不仅锻炼了学生的编程技能，也加深了他们对信号和系统基本概念的理解，如正弦波、阶跃函数、复数表示等。通过实际操作，学生能够掌握MATLAB工具在信号处理中的应用，提升解决问题的能力。