"控制系统数学建模与转换：连续离散、线性非线性、时变定常等"

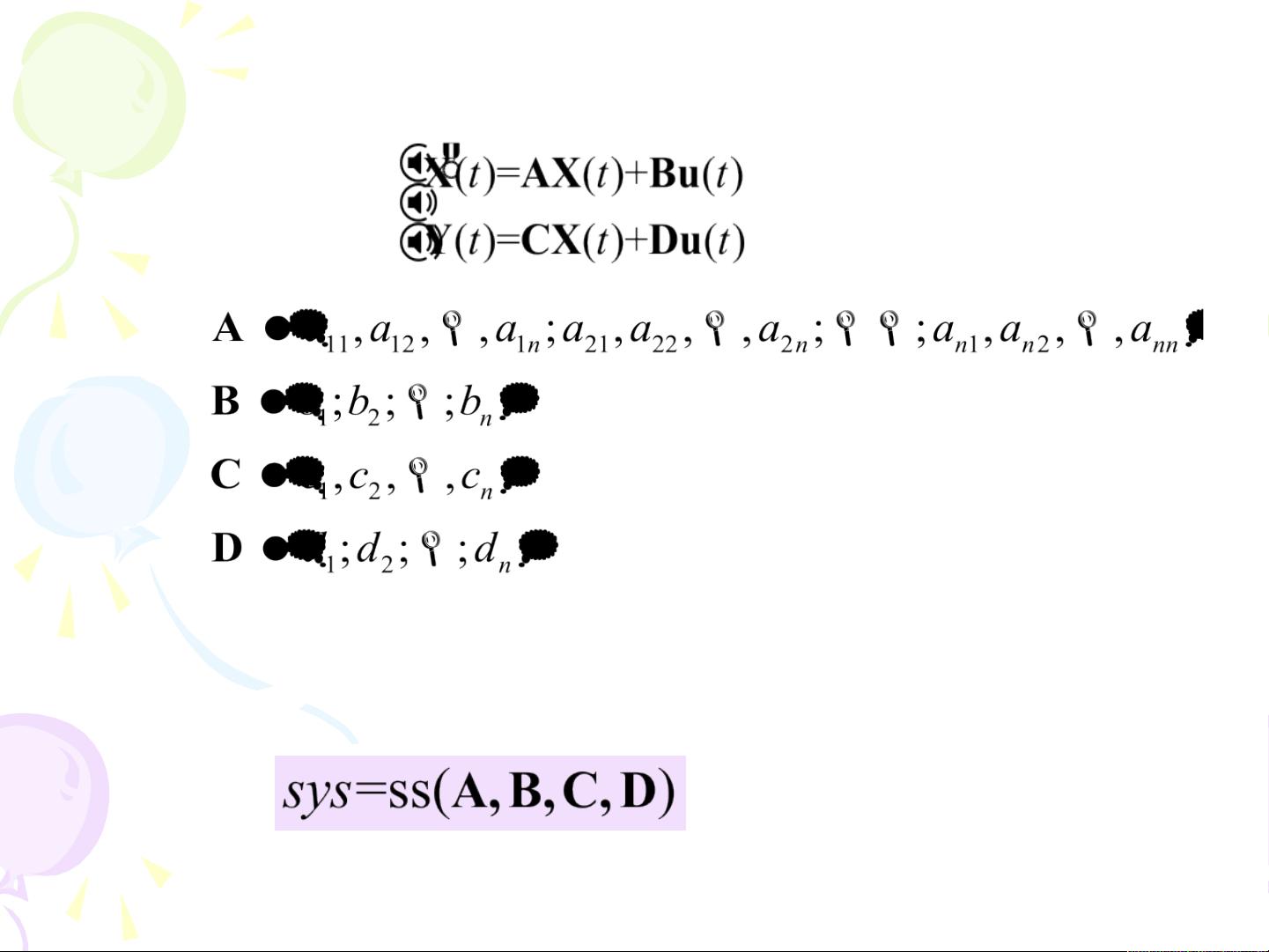
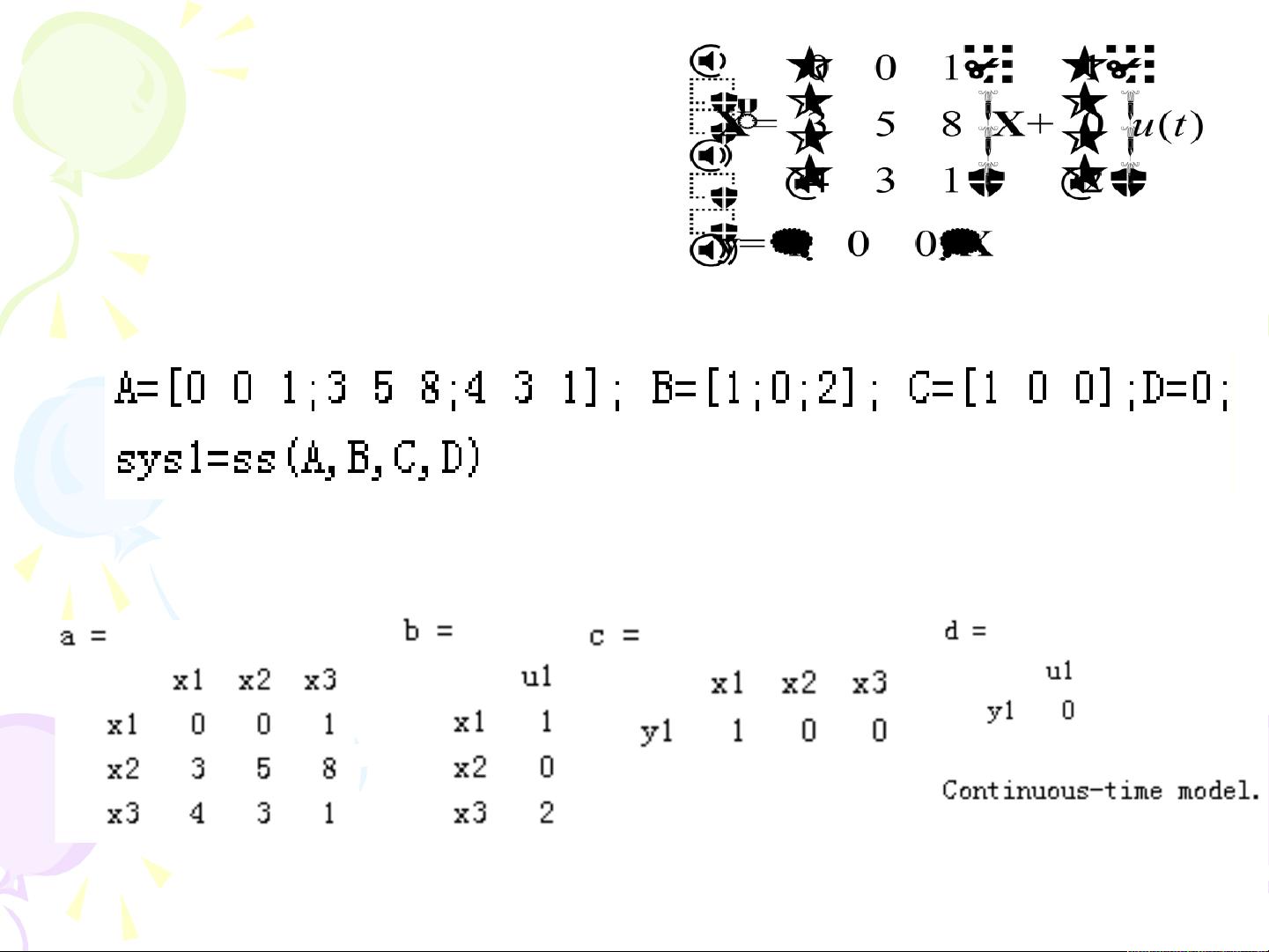
《工学计算机控制系统仿真》PPT中的第4章主要介绍了控制系统的数学模型及其转换以及系统环节模型的连接和标准型实现。在控制系统中，常常使用微分方程模型、传递函数模型、状态空间模型和零极点模型等数学模型。不同的数学模型适用于不同的控制系统场景，掌握模型之间的转换是灵活应用各种数学模型的关键。 控制系统类型方面，本章介绍了连续系统和离散系统、线性系统和非线性系统、时变系统和定常系统（时不变系统）、确定性系统和随机系统。其中，连续系统和离散系统是根据连续时间和离散时间两种不同的控制信号来分类的；线性系统和非线性系统是根据系统的线性性质来分类的；时变系统和定常系统是根据系统参数是否随时间变化来分类的；确定性系统和随机系统是根据系统的输入和输出是否具有随机性质来分类的。 在控制系统中常用的数学模型包括连续系统数学模型和离散系统数学模型。对于线性定常单输入单输出系统（SISO系统），连续系统数学模型可以用系统的微分方程形式来描述，即通过微分方程将系统的输入和输出之间的关系进行建模。而系统的传递函数形式模型则是在零初始条件下，系统输出的拉普拉斯变换与输入的拉普拉斯变换之比。在MATLAB中，可以使用分子、分母多项式系数向量来表示微分方程和传递函数，分子、分母多项式系数向量中的系数按照s的降幂排列。通过printsys()和tf()函数在MATLAB中建立传递函数的系统模型。 除了介绍数学模型之外，本章还涉及了系统数学模型的转换和系统环节模型的连接及标准型实现。系统数学模型的转换是指不同数学模型之间的相互转换，掌握这种转换可以根据具体的需求和场景选择最合适的数学模型。系统环节模型的连接是将多个环节模型进行组合，形成完整的系统模型。标准型实现则是将系统模型转换为最简单和标准化的形式，便于分析和设计控制系统。 总的来说，《工学计算机控制系统仿真》PPT中的第4章介绍了控制系统的数学模型及其转换、系统环节模型的连接和标准型实现等内容。通过学习本章，读者可以了解到不同的控制系统类型和常用的数学模型，并能够掌握模型之间的转换和系统模型的连接与标准化。这些知识对于掌握控制系统的建模和仿真具有重要的指导意义。