华南师大ACM程序设计：最短路径与差分约束系统解析

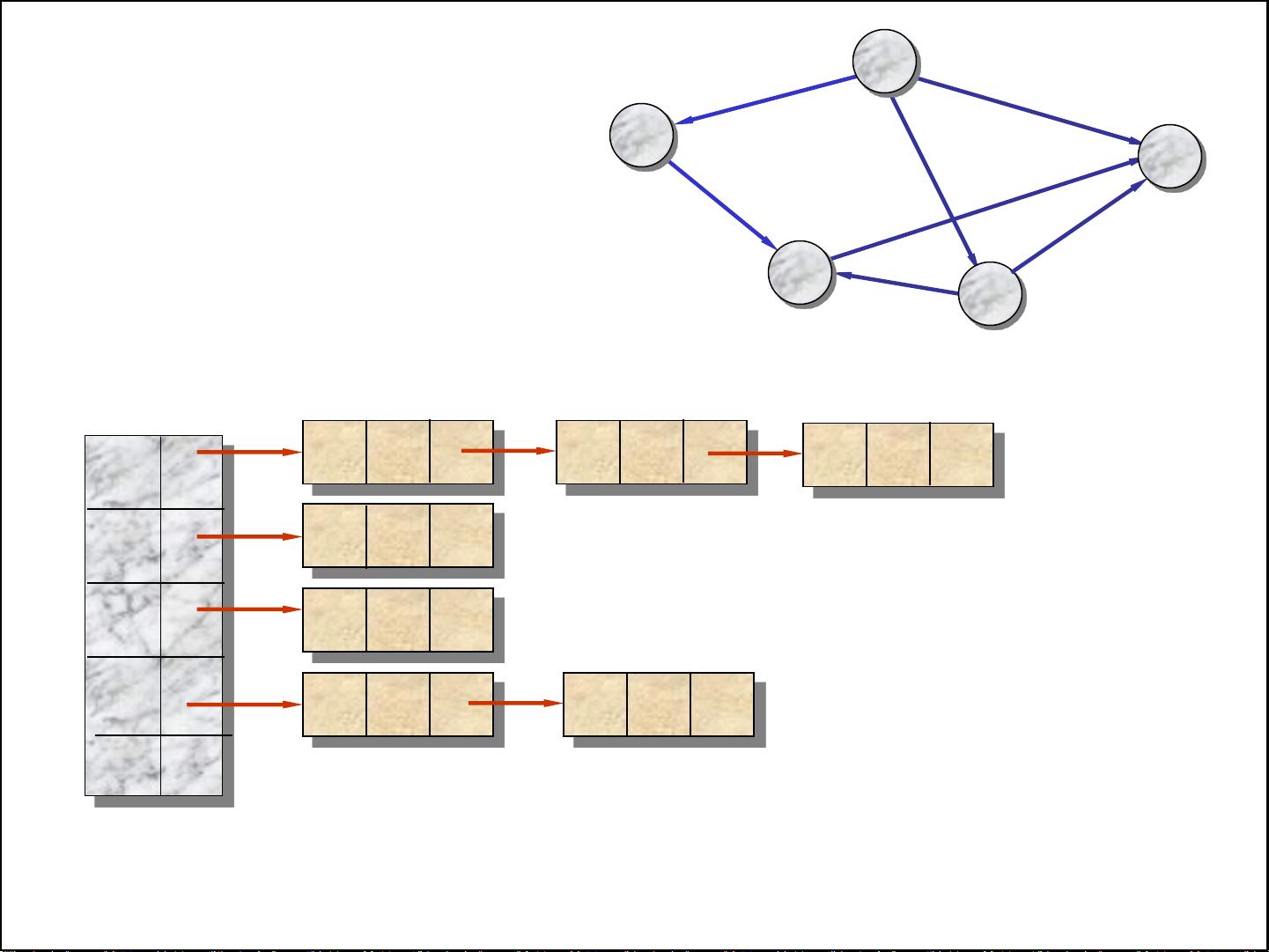
"ACM程序设计课程的讲稿，主要探讨了图论中的最短路径问题以及差分约束系统。这份讲稿来自华南师范大学，通过一个电影情节引入问题，讲述了在面临追捕的情况下如何找到最安全的路径，即最大化不被捕获概率的路线。" 在这份讲稿中，重点讲解了ACM程序设计中与图论相关的内容，特别是如何寻找图中的最短路径。图论是计算机科学中的一个重要分支，它研究如何用图来表示各种关系或结构，并解决其中的问题。在这个场景下，图中的节点代表交叉路口，边则代表连接这些交叉路口的路段。每条边都具有一定的权重，这个权重在这里表示的是从一个交叉路口到达另一个交叉路口时被捕获的概率。 讲稿中提到了输入规格，每个测试用例包含两个整数n和m，分别表示交叉路口的数量和需要考虑的街道数量。n的取值范围是2到100，m的取值范围在1到n*(n-1)/2之间。接下来的m行会详细描述每一条街道，每条街道由三个整数a、b和p定义，a和b表示街道连接的两个交叉路口，p则表示在这条街道上不被捕获的概率，取值范围在1到100之间。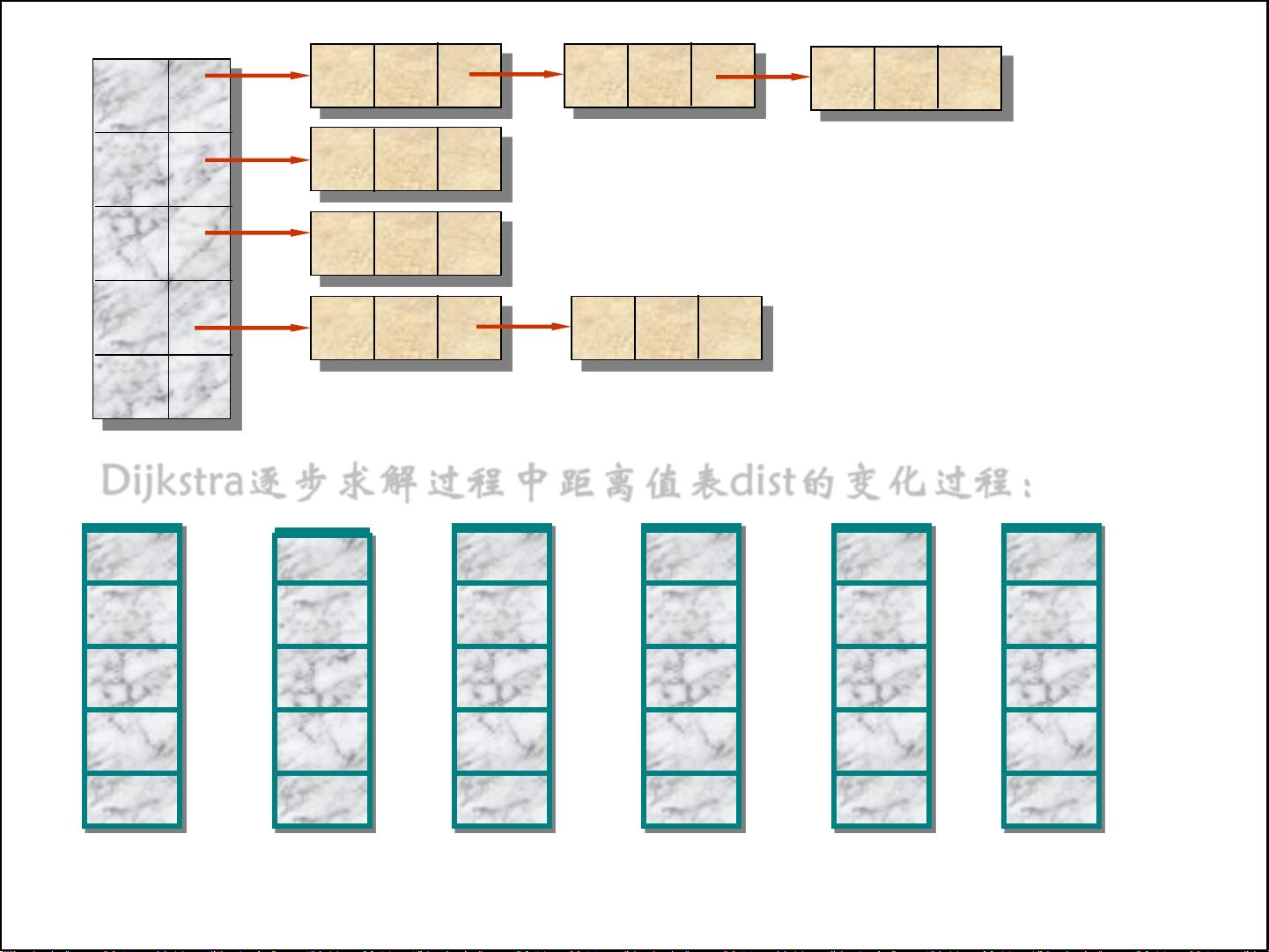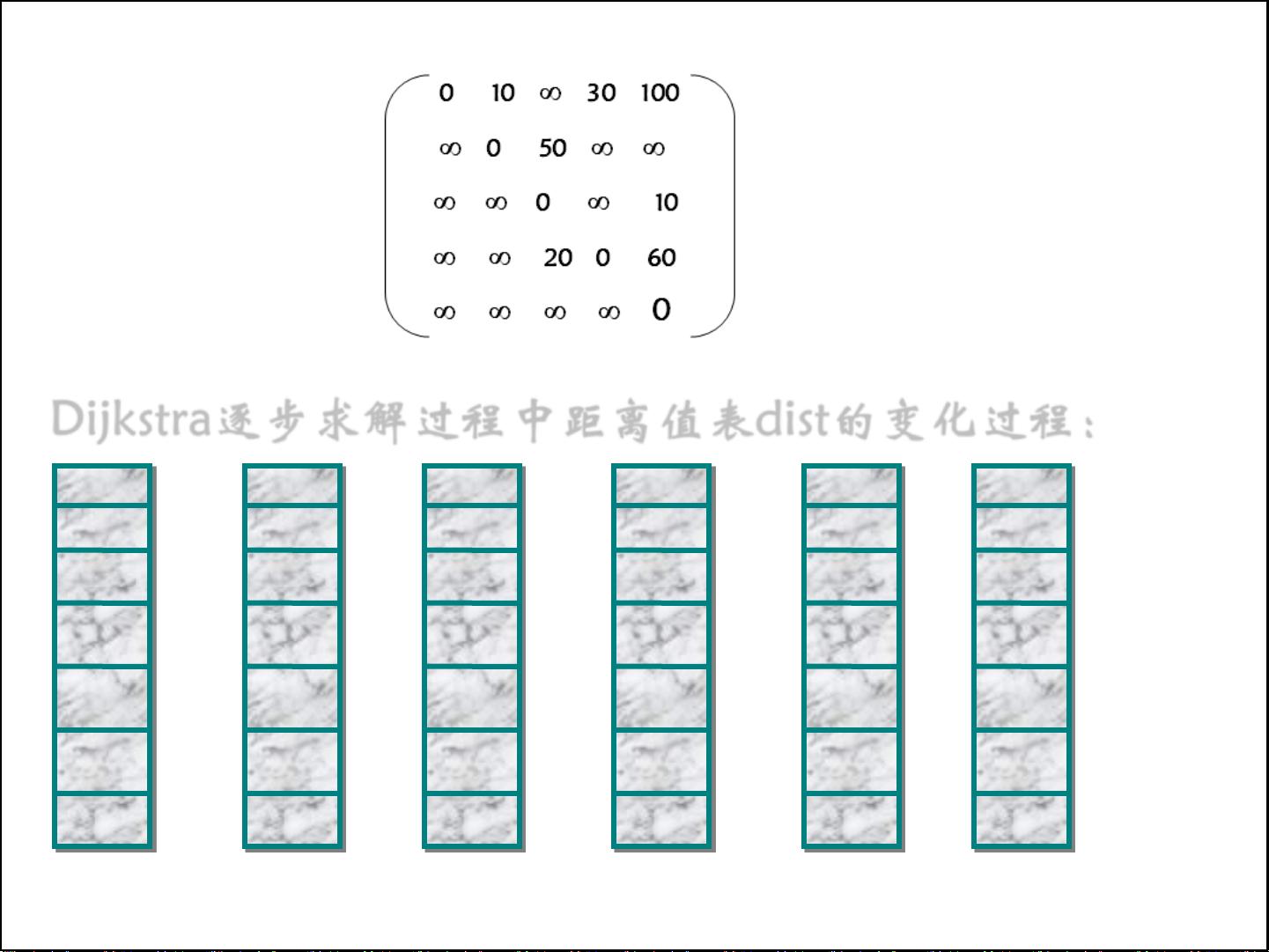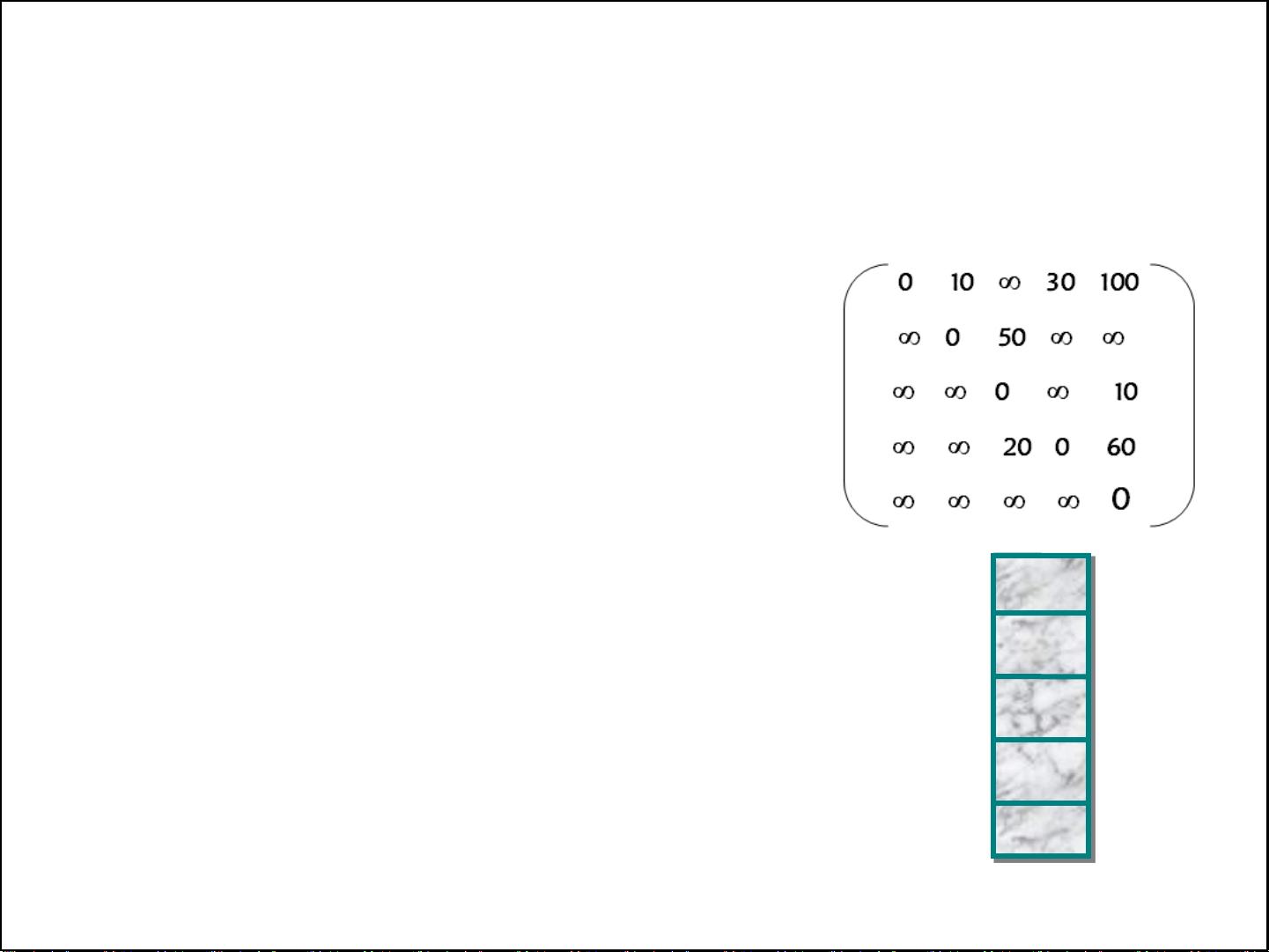 寻找最安全的路径，实际上是一个优化问题，需要最大化整个路径上的总概率。这通常涉及到动态规划或者网络流算法，如Dijkstra算法、Floyd-Warshall算法或Bellman-Ford算法等，但根据问题的设定，可能需要针对概率进行特殊处理，例如使用期望值或者加权平均。 差分约束系统（Difference Constraints System）在解决此类问题时也可能会派上用场，特别是在路径优化和调度问题中。差分约束系统可以用来描述变量之间的关系，通过线性规划或迭代方法求解最优解。在这个问题中，可能需要建立一个差分约束模型，来确保路径的选择能够使总被捕获概率最小。 这份讲稿提供了关于图论中最短路径问题的实际应用，以及如何在ACM程序设计竞赛中解决这类问题的思路。对于学习ACM竞赛或者图论的初学者来说，这是一份非常有价值的参考资料。