Improved Unified Architecture for 3, 5, and 7-point
Winograd Fourier Transform Algorithm
Qiang Zhang, Changyin Liu, Peng Zhang, Yuanzhi Chen, Jianhe Du
School of Information and Communication Engineering
Communication University of China
Beijing, China
qiangzhang@cuc.edu.cn, liuchy@cuc.edu.cn, zhangpeng@cuc.edu.cn, chenyuanzhi@cuc.edu.cn, dujianhe1@gmail.com
Abstract—This paper proposes an improved unified
architecture for 3, 5, and 7-point Winograd Fourier Transform
Algorithm (WFTA). We define the mapping rules of inputs and
outputs and modify the matrices in WFTA by matrix
transformation. This design not only reduces hardware resource
consumption by reducing multiplexers from 7 to 3, but also
simplifies the control flow by performing data input and ports
mapping through certain rules.
Keywords—WFTA; unified architecture; simplified control
flow
I. INTRODUCTION
Orthogonal Frequency Division Multiplexing (OFDM)
technology, which has strong immunity to frequency selective
fading, is widely used in modern wireless communication
systems. One of its core technologies is the DFT. In general,
FFT is used to reduce the complexity of the DFT.
FFT can be divided into two categories: power-of-two and
non-power-of-two. For power-of-two FFTs, algorithm
simulation and hardware implementation are very mature.
Currently, some standards involve non-power-of-two FFTs.
E.g., 3G Long Term Evolution (LTE) involves 1536-point
DFT
[1]
, Chinese Digital Terrestrial/Television Multimedia
Broadcasting (DTMB) involves 3780-point DFT
[2]
, and Digital
Radio Mondiale (DRM) involves 228-point DFT
[3]
. Non-
power-of-two FFTs are mostly calculated using Cooley-Tukey
Algorithm and Prime Factor Algorithm (PFA) to decompose an
N-point DFT into smaller DFTs, which are calculated by the
Winograd Fourier Transform Algorithm (WFTA). E.g., for
DTMB, 3780-point is decomposed into 3, 4, 5, 7, and 9-point
[4,
5]
.
WFTA calculates small point DFTs through matrix
decomposition, which greatly reduces the number of
multiplications. References [4] and [5] need to use different
circuits to calculate different small point WFTAs, and the
architecture is not uniform. Reference [6] proposed a unified
architecture of 2, 3, 4, 5, and 7-point WFTA. It can calculate 2,
3, 4, 5, and 7-point WFTA in the same circuit, reducing
resource consumption. However, it is just a blunt combination
of 2, 3, 4, 5 and 7-point signal flow graph. The input data and
ports mapping have no regularity, which leads to complicated
timing control. We think that 2 and 4-point DFTs needs 4
adders to achieve, which takes less resources. So there are no 2
and 4-point in the improved unified architecture. When using
the architecture in reference [6] for 3, 5, and 7-point WFTA, 36
complex adders, 16 real multipliers and 7 multiplexers are
needed, which results in great circuit differences and complex
control flow.
Section II introduces N-point WFTA. The improved unified
architecture design of N-point WFTA is proposed in the section
III. The last section concludes the paper.
II. N-
POINT WFTA
N-point WFTA can be expressed as:
T T
01 -101 -1
== ,
X CBA
N
N
xxXxXX ΛΛ
( 1 )
where A is an M × N matrix related to the input (M ≥ N), C is
the N×M matrix associated with the output, B is an M×M
diagonal matrix about θ (θ = 2/N), and the diagonal element is
denoted as {B
0
= 1, B
1
, ..., B
M -1
}, where B
1
, …, B
M-1
are purely
real or purely imaginary.
For 3-point WFTA, M = 3, N = 3, and the Winograd
algorithm gives the following matrices
11 1 1 0 0 10 0
=01 1, =0cos 1 0 , =11-1 .
01-1 0 0 j
2/3
2/3sin 1 1 1
AB C
(2)
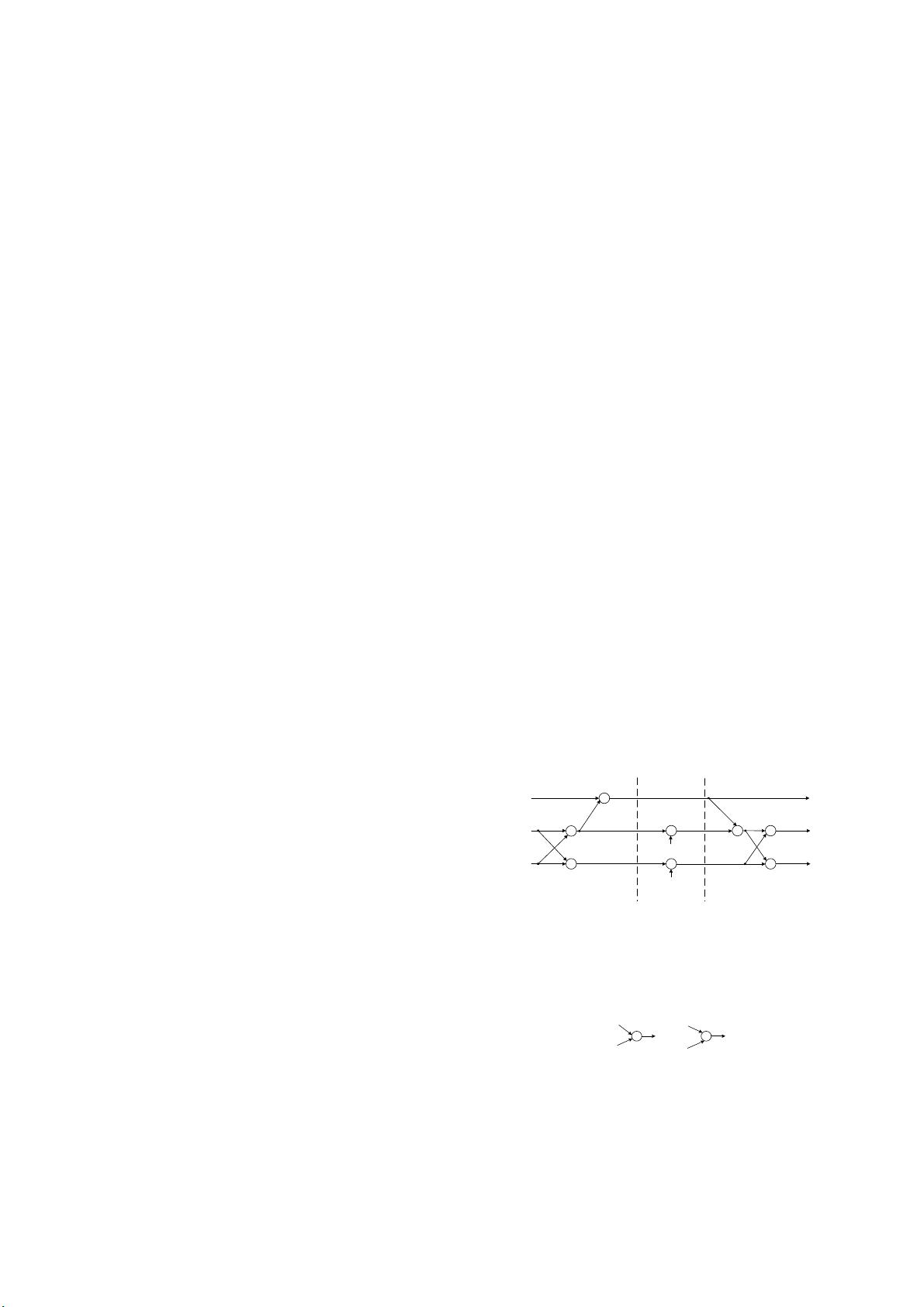
Bringing (2) into (1), we can get a 3-point WFTA signal
flow graph, as shown in Fig. 1. It can be seen that 3-point
WFTA involves 6 complex adders and 4 real multipliers.
x
0
+
x
1
-
-
x
2
B
2
B
1
× X
1
X
2
+
X
0
+
× +
a = A[x
0
x
1
x
2
]
T
b=Ba
[X
0
X
1
X
2
]
T
=Cb
Ⅰ Ⅱ Ⅲ
Fig. 1 3-point WFTA signal flow graph
The operation rules of the adder in Fig. 1 is explained in
Fig. 2. The input of the upper branch minus the input of the
lower branch is shown in Fig. 2(a). The addition is shown in
Fig. 2(b).
‐
S
0
=U
0
−D
0
(a)
+
S
1
=U
1
+D
1
(b)
U
0
D
0
S
0
U
1
D
1
S
1
Fig. 2 Symbol description
978-1-7281-0513-0/19/$31.00 ©2019 IEEE
2019 IEEE 3rd Advanced Information Management,Communicates,Electronic and Automation Control Conference (IMCEC 2019)









