神经网络基础：从M-P神经元模型到正则化

"本文主要介绍了神经网络的基本概念和神经元模型，强调了正则化在防止过拟合中的重要作用，并简述了M-P神经元模型的结构和激活函数的使用，特别是Sigmoid函数的特性。" 在机器学习领域，神经网络是一种模仿生物神经系统的结构和功能的模型，用于处理各种复杂的学习任务。正则化是神经网络中一个至关重要的概念，其目的是通过在损失函数中加入惩罚项来控制模型的复杂度，避免过拟合现象。在训练过程中，正则化使网络在试图最小化预测误差的同时，也要最小化权重参数的大小，从而达到平衡模型性能和泛化能力的效果。 神经网络的基本组成单元是神经元，它们通过复杂的连接方式形成网络。生物神经元具有树突、轴突和细胞体等结构，而在数学模型中，神经元被简化为M-P神经元模型。这个模型接受多个输入信号，每个信号都带有相应的权重，这些加权后的输入信号汇总后与神经元的阈值进行比较。如果总输入超过阈值，神经元会输出一个信号，否则不输出。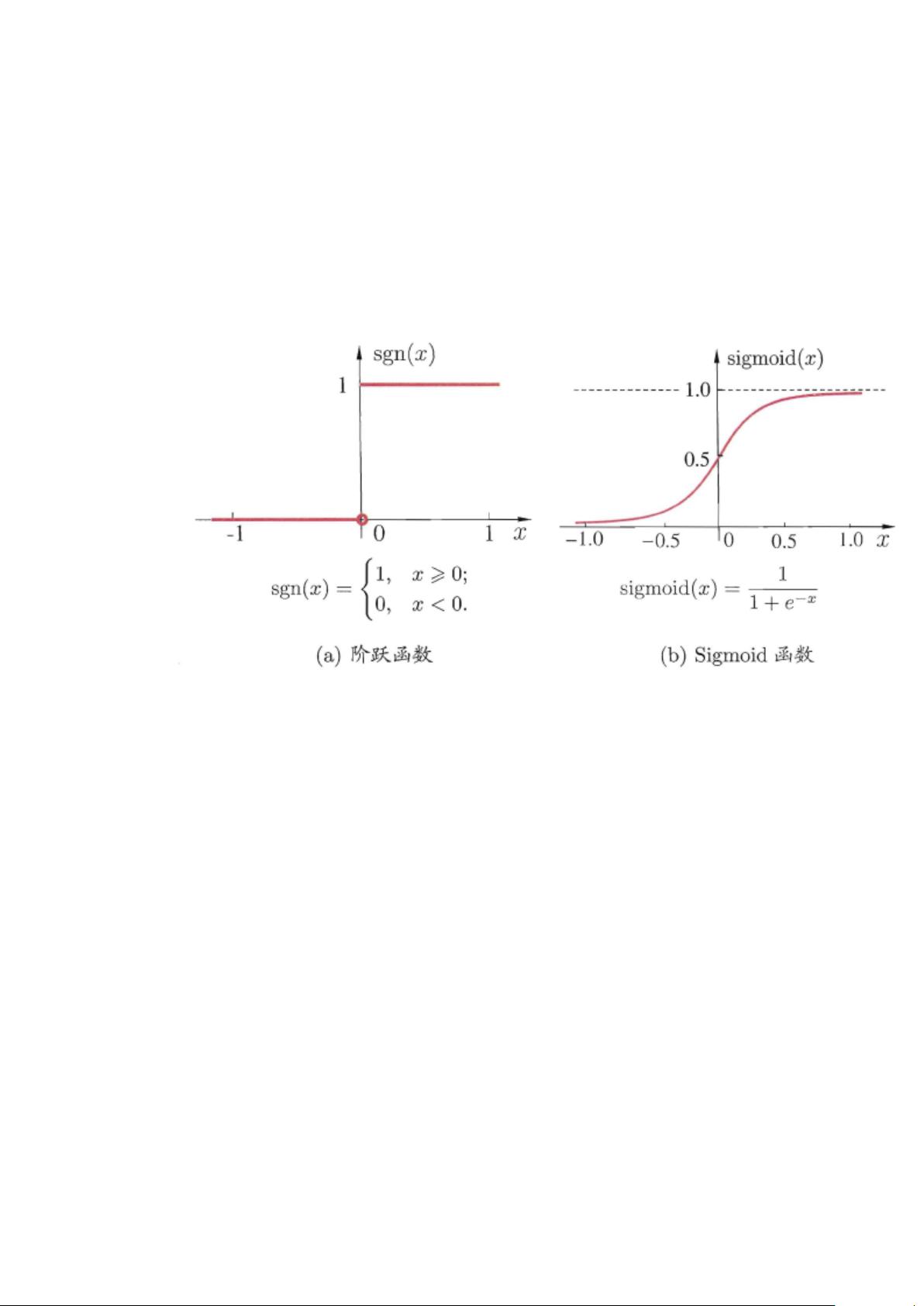 激活函数在神经元模型中起到关键作用，它决定了神经元何时被激发。早期的M-P神经元模型使用了阶跃函数，但由于其非连续性和不光滑性，实际应用中往往采用Sigmoid函数作为替代。Sigmoid函数可以将实数范围内的输入值压缩到(0,1)之间，提供了连续且可微的输出，有利于网络的梯度下降优化过程。 Sigmoid函数的输出值可以解释为神经元的激活程度或概率，对于二分类问题，0.5通常作为分类的阈值。然而，Sigmoid函数在输入接近正负无穷时导数值非常小，可能导致梯度消失的问题，因此在现代深度学习中，人们更倾向于使用ReLU（Rectified Linear Unit）及其变种，如Leaky ReLU和ELU，这些激活函数在解决梯度消失问题上表现更好。 神经网络通过正则化和合理的神经元模型来实现高效学习和泛化，而激活函数的选择则直接影响网络的表达能力和训练效果。随着研究的深入，神经网络模型和理论不断发展，如深度学习、卷积神经网络和循环神经网络等，为各种复杂问题的解决提供了强大的工具。