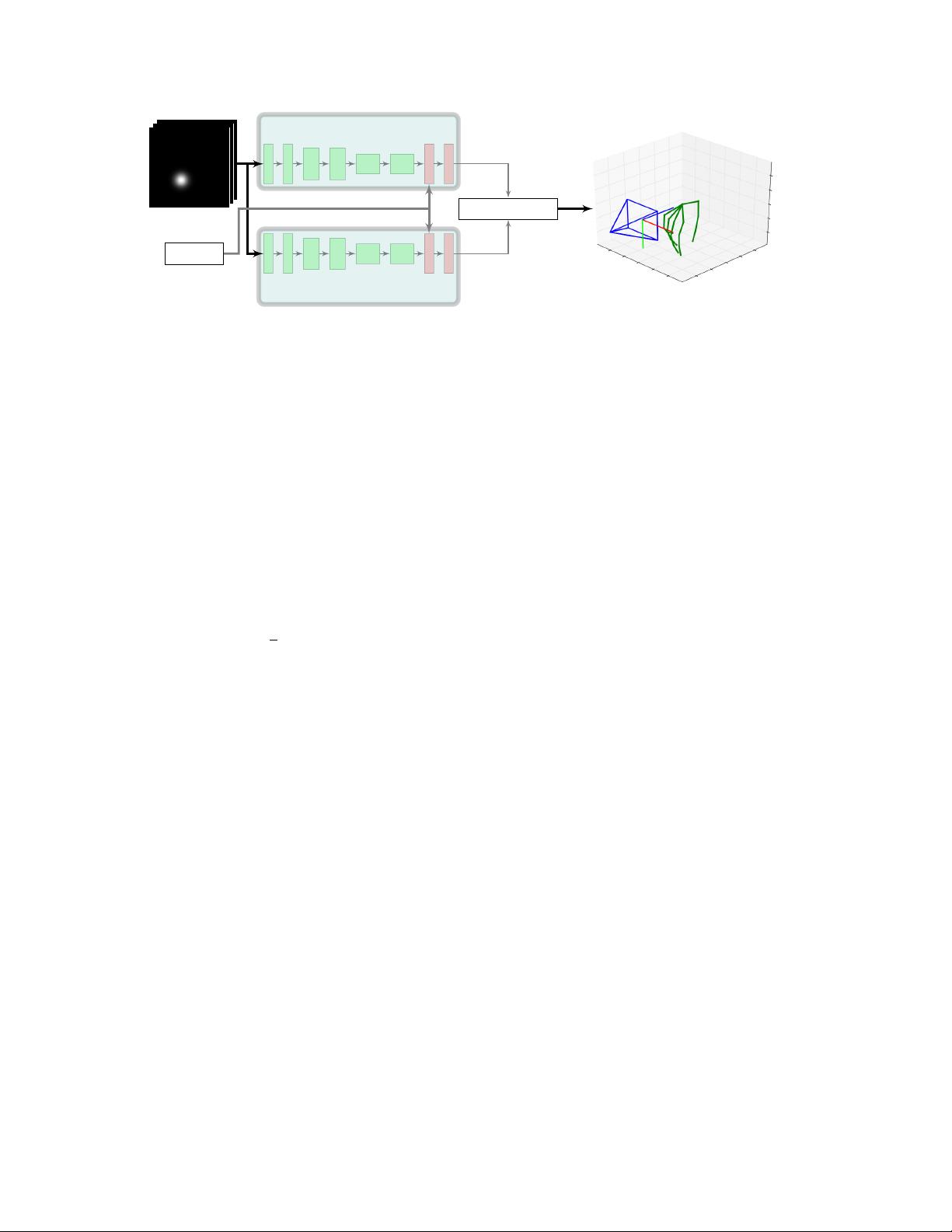
Canonical Coordinates
Viewpoint
left/right
w
rel
= w
c
· R
>
R
w
c
w
rel
Figure 3: Proposed architecture for the PosePrior network. Two almost symmetric streams estimate canonical coordinates
and the viewpoint relative to this coordinate system. Combination of the two predictions yields an estimation for the relative
normalized coordinates w
rel
.
3. Hand pose representation
Given a color image I ∈ R
N ×M ×3
showing a single
hand, we want to infer its 3D pose. We define the hand pose
by a set of coordinates w
i
= (x
i
, y
i
, z
i
), which describe the
locations of J keypoints in 3D space, i.e., i ∈ [1, J] with
J = 21 in our case.
The problem of inferring 3D coordinates from a single
2D observation is ill-posed. Among other ambiguities, there
is a scale ambiguity. Thus, we infer a scale-invariant 3D
structure by training a network to estimate normalized co-
ordinates
w
norm
i
=
1
s
· w
i
, (1)
where s = kw
k+1
− w
k
k
2
is a sample dependent constant
that normalizes the distance between a certain pair of key-
points to unit length. We choose k such that s = 1 for the
first bone of the index finger.
Moreover, we use relative 3D coordinates to learn a
translation invariant representation of hand poses. This is
realized by subtracting the location of a defined root key-
point. The relative and normalized 3D coordinates are given
by
w
rel
i
= w
norm
i
− w
norm
r
(2)
where r is the root index. In experiments the palm keypoint
was the most stable landmark. Thus we use r = 0.
4. Estimation of 3D hand pose
We estimate three-dimensional normalized coordinates
w
rel
from a single input image. An overview of the general
approach is provided in Figure 2. In the following sections,
we provide details on its components.
4.1. Hand segmentation with HandSegNet
For hand segmentation we deploy a network architecture
that is based on and initialized by the person detector of Wei
et al. [19]. They cast the problem of 2D person detection as
estimating a score map for the center position of the hu-
man. The most likely location is used as center for a fixed
size crop. Since the hand size drastically changes across
images and depends much on the articulation, we rather
cast the hand localization as a segmentation problem. Our
HandSegNet is a smaller version of the network from Wei
et al. [19] trained on our hand pose dataset. Details on the
network architecture and its training prcedure are provided
in the supplemental material. The hand mask provided by
HandSegNet allows us to crop and normalize the inputs in
size, which simplifies the learning task for the PoseNet.
4.2. Keypoint score maps with PoseNet
We formulate localization of 2D keypoints as estimation
of 2D score maps c = {c
1
(u, v), . . . , c
J
(u, v)}. We train a
network to predict J score maps c
i
∈ R
N ×M
, where each
map contains information about the likelihood that a certain
keypoint is present at a spatial location.
The network uses an encoder-decoder architecture simi-
lar to the Pose Network by Wei et al. [19]. Given the image
feature representation produced by the encoder, an initial
score map is predicted and is successively refined in resolu-
tion. We initialized with the weights from Wei et al. [19],
where it applies, and retrained the network for hand key-
point detection. A complete overview over the network ar-
chitecture is located in the supplemental material.
4.3. 3D hand pose with the PosePrior network
The PosePrior network learns to predict relative, nor-
malized 3D coordinates conditioned on potentially incom-
plete or noisy score maps c(u, v). To this end, it must learn
the manifold of possible hand articulations and their prior
probabilities. Conditioned on the score maps, it will output
the most likely 3D configuration given the 2D evidence.
Instead of training the network to predict absolute 3D co-
ordinates, we rather propose to train the network to predict
coordinates within a canonical frame and additionally esti-









