优化数据结构：AVL树与平衡二叉操作详解

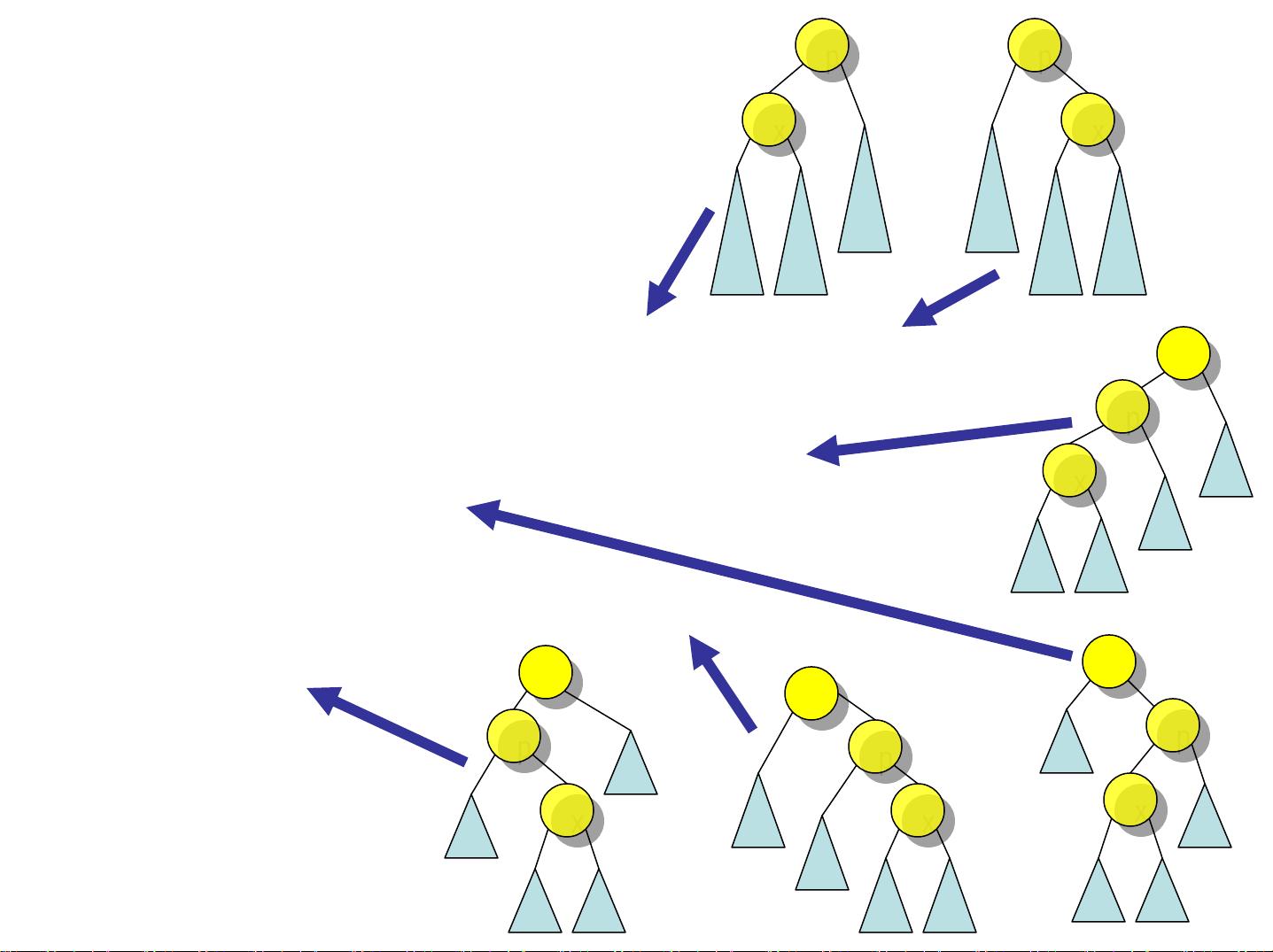
高级数据结构是计算机科学中的重要概念，特别是在算法设计和项目开发中起着核心作用。本课程由刘汝佳教授讲解，主要涵盖了平衡二叉树、可并优先队列、线段树和树状数组基础，以及RMQ与LCA等高级主题。 首先，平衡二叉树（如基本BST）是一种特殊的二叉搜索树，其特点是每个节点的左子树小于根节点，右子树大于根节点。基本实现中，查找、插入和删除操作的时间复杂度分别为O(h)，其中h表示树的高度。由于不平衡的树可能导致这些操作效率降低，因此保持树的平衡至关重要。一个平衡的树在渐进意义上，其高度为O(logn)，这意味着随着结点数量的增长，操作速度会保持高效。 AVL树是平衡二叉树的一种，它通过限制每个节点的左右子树高度差不超过1来确保平衡。AVL树的高度可以通过斐波那契数列近似表示，即最大高度h与结点数n之间的关系为S(n)~1.44logn。当树变得不平衡时，通过旋转操作进行调整，包括单旋转和双旋转，以恢复平衡。插入新元素时，算法需找到第一个不平衡的祖父节点，根据其与孙子节点的关系进行适当的旋转。 接下来，课程还介绍了可并优先队列，一种特殊的数据结构，用于处理优先级任务。它的特点是可以同时合并两个优先队列，同时保持队列的优先级特性。线段树和树状数组是用于高效查询区间和范围操作的数据结构，它们在解决区间查询问题时表现出色，常用于求解RMQ（Range Minimum Query）和LCA（Least Common Ancestor）等问题。 高级数据结构的学习对于提升编程技巧和解决复杂算法问题至关重要。理解并掌握这些数据结构能够帮助开发者设计出更高效的程序，尤其是在ACM竞赛或实际项目开发中，能够显著提高代码的性能和可维护性。