SVD分解详解:从直观到几何意义
需积分: 0 2 浏览量
更新于2024-08-05
1
收藏 383KB PDF 举报
"SVD分解的理解 | 计算机视觉博客"
奇异值分解(Singular Value Decomposition, SVD)是线性代数中的一个重要概念,尤其在计算机视觉领域有着广泛的应用。SVD能够将一个矩阵分解成三个矩阵的乘积:U * Σ * V^T,其中U和V是正交矩阵,Σ是对角矩阵。这种分解方式不仅理论上有深刻的意义,而且在实际问题中非常实用。
在计算机视觉中,SVD常用于图像处理、特征提取和降维等多个方面。例如,它可以用来分析图像的结构信息,通过分解可以得到图像的主要成分,这对于理解和压缩图像数据非常有帮助。此外,SVD还能用于主成分分析(PCA),这是一种常见的数据降维技术,可以将高维数据映射到低维空间,同时保持数据集中的大部分方差。
对于一个矩阵A,SVD的几何解释如下:
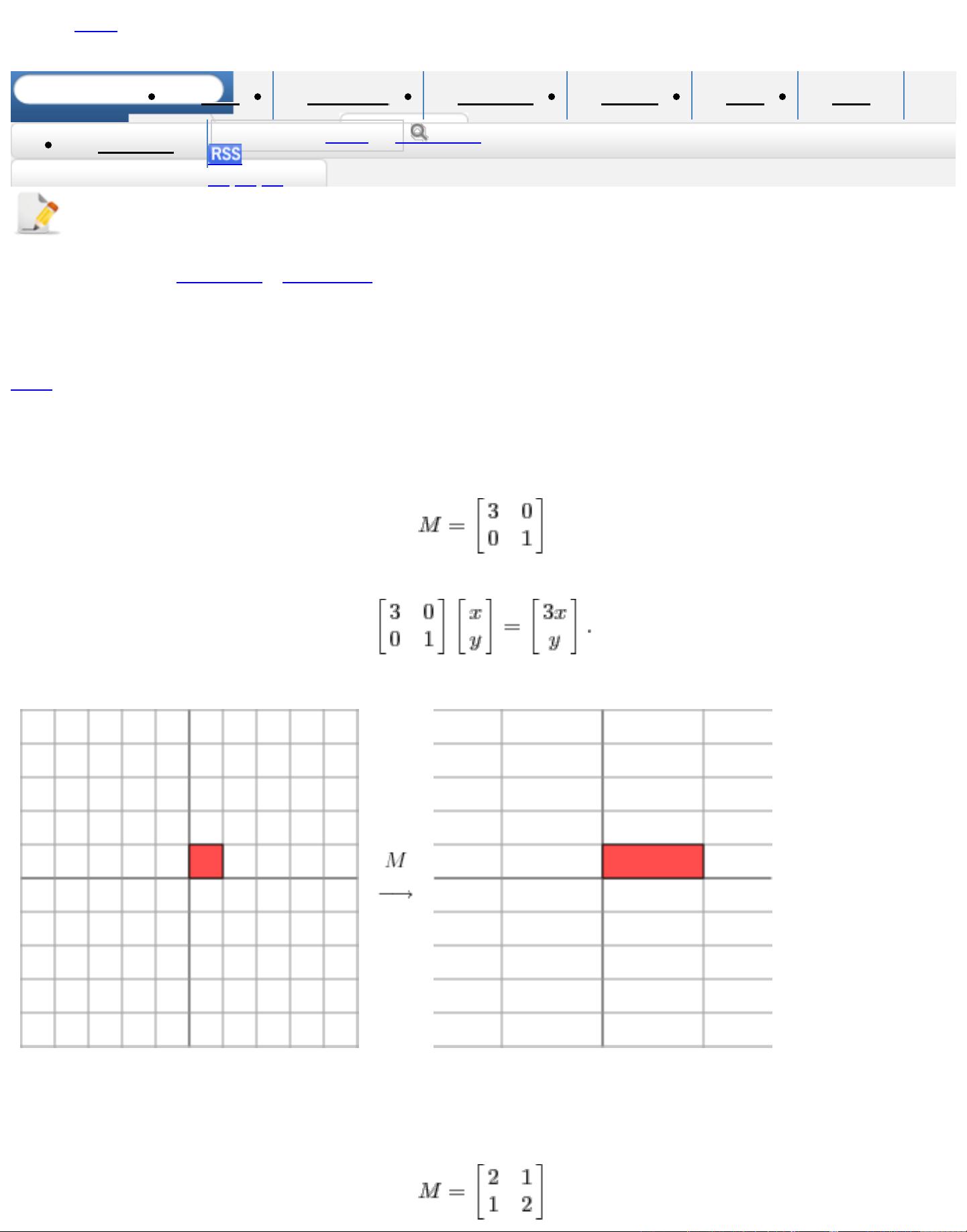
1. 旋转:U矩阵代表了从原坐标系到一个新的正交坐标系的旋转。每一列向量u_i是原坐标系中的基向量在新坐标系中的表示。
2. 尺度拉伸:Σ矩阵是对角矩阵,对角线上的元素σ_i是奇异值,它们代表了数据在各个方向上的拉伸或压缩程度。σ_i越大,对应的方向上数据变化越大;σ_i越小,对应的方向上数据变化越小。
3. 再次旋转:V^T矩阵则表示从新坐标系回转到原坐标系,使得原始数据在新坐标系下的拉伸和压缩可以清楚地看到。
以对称矩阵为例,由于对称矩阵的特性,它们总是可以被对角化,即存在一组正交基,使得矩阵在这些基下的表示是对角的。特征向量v_i和对应的特征值λ_i满足Mv_i = λ_i v_i,特征值λ_i对应于对角矩阵Σ上的元素。
非对称矩阵的SVD并不直接给出对角化,但依然提供了对数据变化的直观理解。例如,一个剃刀(shear)效应的矩阵可以通过旋转坐标系使得变换在新的正交坐标系下变得更简单。在这种情况下,虽然不能完全对角化,但SVD仍然能找到一组正交基,使得矩阵在这些基下的作用更易于理解。
SVD分解在计算机视觉中的具体应用包括但不限于:
- 图像去噪:通过保留具有较大奇异值的成分,忽略小的奇异值,可以去除噪声并保留主要图像特征。
- 图像恢复与压缩:SVD可以帮助恢复损坏的图像,也可以用于有损压缩,只保留重要的奇异值以减小存储需求。
- 相机标定:在多视图几何中,SVD可用于解算单应性矩阵,进而计算相机参数。
- 人脸识别:SVD可以用于PCA-Eigenface方法,通过降维来捕获人脸的关键特征。
SVD是理解复杂矩阵操作的强大工具,它的应用远远超出了这个简单的解释,深入到许多复杂的机器学习和计算机视觉算法中。理解SVD对于解决涉及矩阵运算的问题至关重要。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2020-01-11 上传
2021-10-04 上传
2021-06-08 上传
2023-06-06 上传
2023-05-23 上传
2022-02-20 上传
茶啊冲的小男孩
- 粉丝: 30
- 资源: 326
最新资源
- 全国江河水系图层shp文件包下载
- 点云二值化测试数据集的详细解读
- JDiskCat:跨平台开源磁盘目录工具
- 加密FS模块:实现动态文件加密的Node.js包
- 宠物小精灵记忆配对游戏:强化你的命名记忆
- React入门教程:创建React应用与脚本使用指南
- Linux和Unix文件标记解决方案:贝岭的matlab代码
- Unity射击游戏UI套件:支持C#与多种屏幕布局
- MapboxGL Draw自定义模式:高效切割多边形方法
- C语言课程设计:计算机程序编辑语言的应用与优势
- 吴恩达课程手写实现Python优化器和网络模型
- PFT_2019项目:ft_printf测试器的新版测试规范
- MySQL数据库备份Shell脚本使用指南
- Ohbug扩展实现屏幕录像功能
- Ember CLI 插件:ember-cli-i18n-lazy-lookup 实现高效国际化
- Wireshark网络调试工具:中文支持的网口发包与分析