非正弦周期电流电路分析：傅里叶级数与谐波

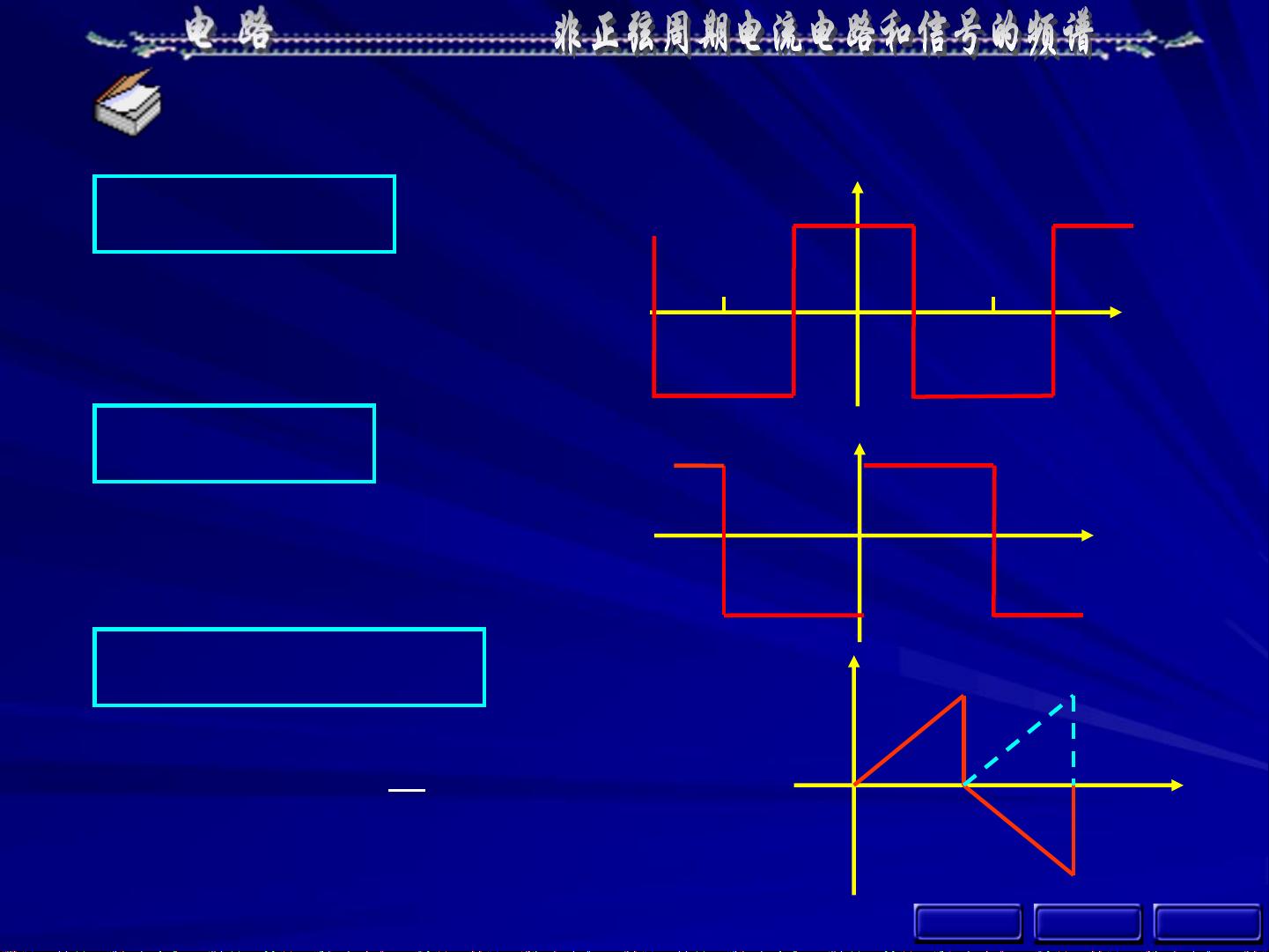
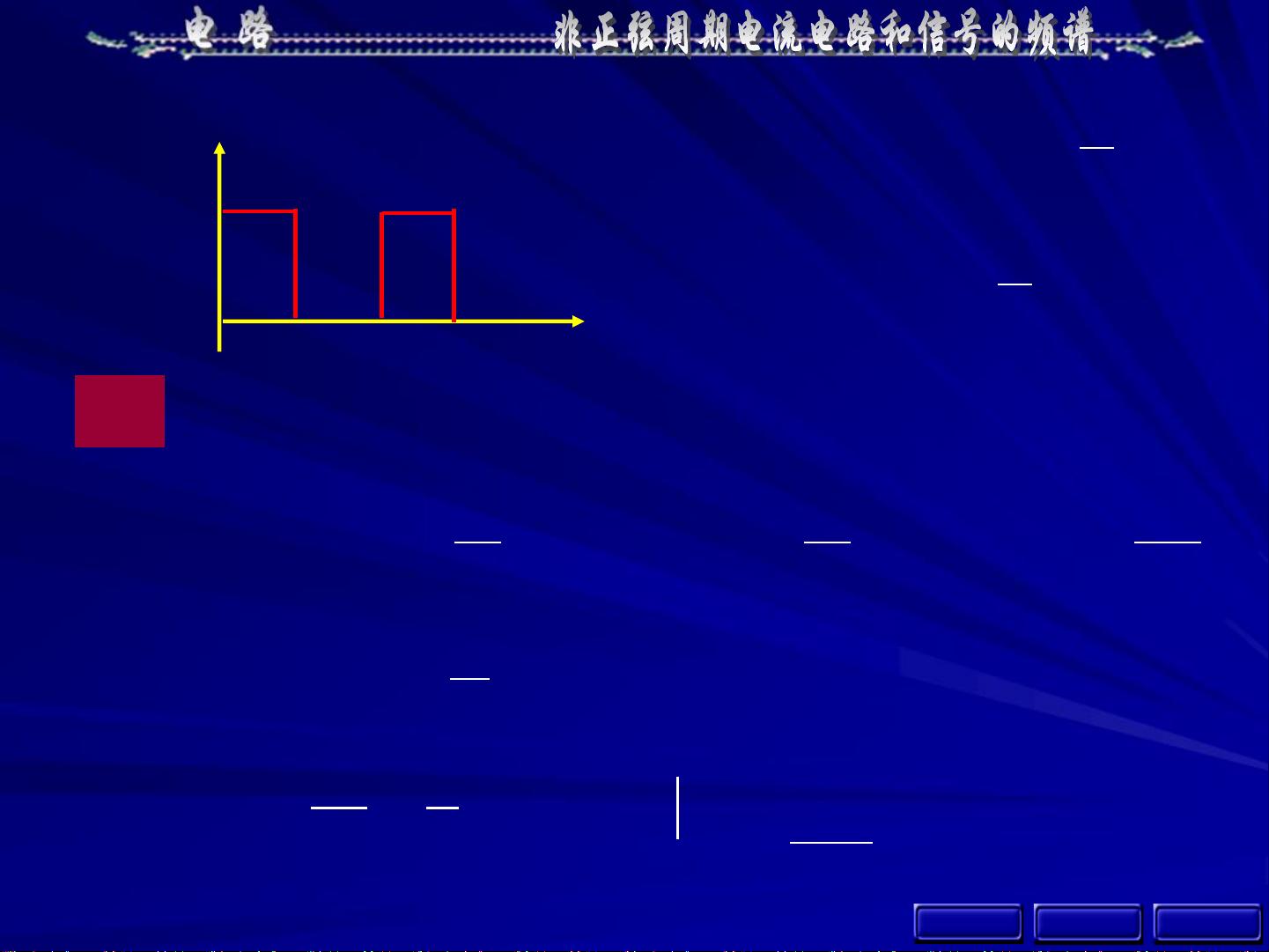
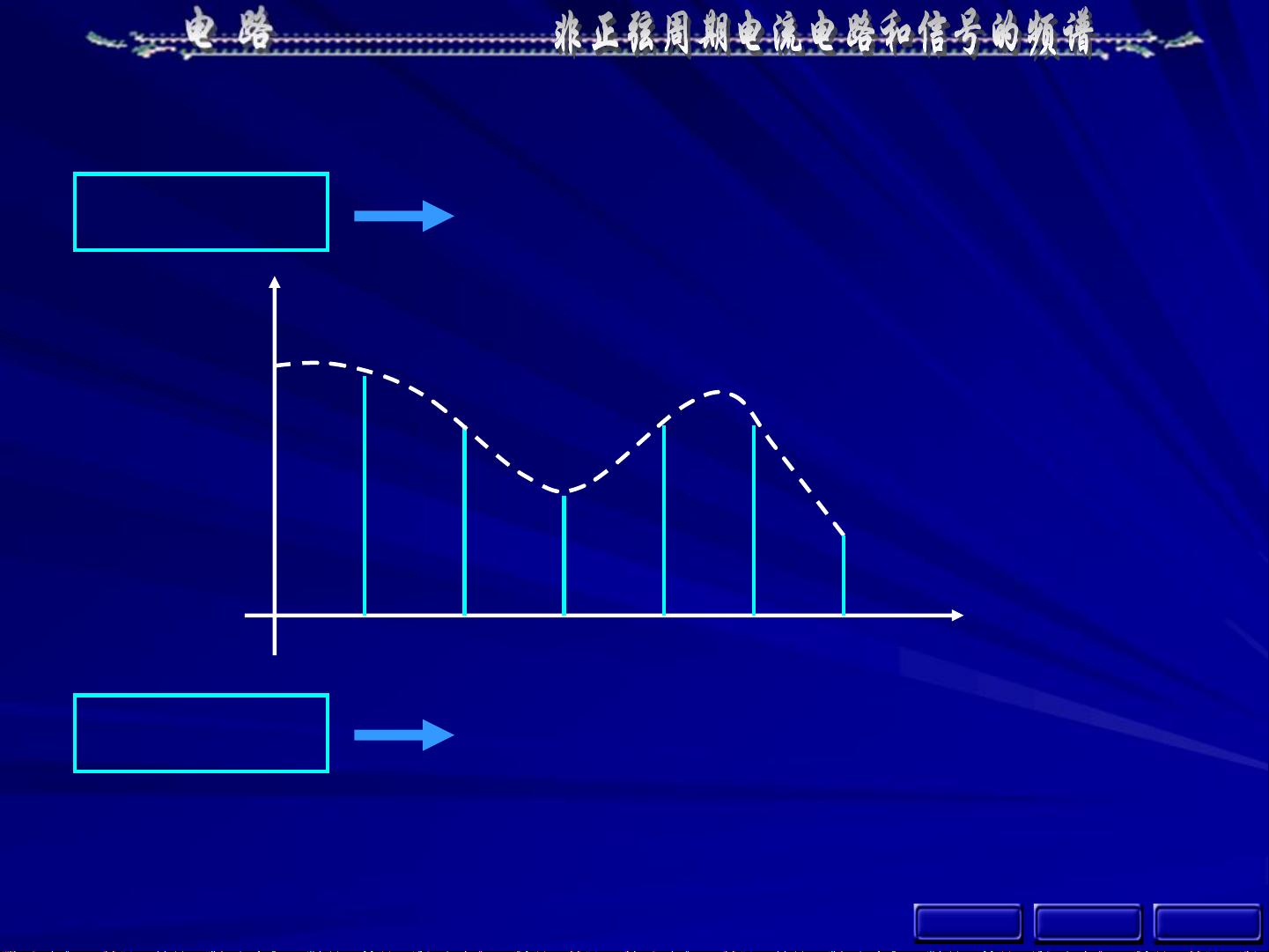
"第13章 非正弦周期电流电路" 在电力系统和电子技术领域中，非正弦周期电流电路是一个重要的研究主题。本章内容主要围绕非正弦周期信号的特性、分析方法及其在实际应用中的表现进行深入探讨。 13-1 非正弦周期信号 非正弦周期信号是指不遵循简单正弦波规律的周期性电信号，常见于多种工程场景。例如，半波整流电路的输出、示波器的水平扫描电压、脉冲电路中的脉冲信号以及交、直流共存电路等。这些信号的特点是它们不是单一频率的正弦波，而是由多个不同频率的正弦波成分叠加而成，且按照一定的周期规律变化。 13-2 非正弦周期函数分解为傅里叶级数 傅里叶级数是一种数学工具，用于将任意周期函数表示为一组简谐波（正弦和余弦函数）的线性组合。一个周期函数如果满足狄里赫利条件（周期性、有限极值点和绝对可积性），就可以被分解为傅里叶级数。傅里叶级数包含直流分量（平均值）、基波（与原函数相同频率的正弦波）以及一系列的谐波（包括二次谐波、三次谐波等高次谐波）。每个谐波都有其特定的幅度A_k和相位φ_k，与频率ω_k相关。 13-3 非正弦周期电流电路的计算 在电路分析中，非正弦周期电流电路的计算涉及到有效值、平均值和平均功率的求解。有效值是衡量交流电等效于直流电的标准，它反映了电流或电压在一段时间内的平均效果。平均值则用于计算非正弦电流或电压在一个周期内的平均效应。平均功率是设备在非正弦周期信号下消耗的功率。理解这些概念对于设计和分析电力系统至关重要。 13-4 对称三相电路中的高次谐波 在对称三相电路中，除了基波之外，还可能存在高次谐波。这些谐波可能会引起系统的效率降低、设备过热、线路损耗增加等问题，因此需要通过滤波或其他补偿技术来减少其影响。 *13-5 傅里叶级数的指数形式 傅里叶级数也可以表示为指数形式，即复指数函数的系列，这在某些分析和计算中更加便捷。 *13-6 傅里叶积分简介 傅里叶积分是傅里叶级数的连续形式，它将非周期函数转换为频域表示，有助于理解信号的频谱特性。 *13-7 2.非正弦周期函数的有效值和平均功率 有效值和平均功率的概念同样适用于非正弦周期函数，它们是分析非正弦电流电路的关键参数，可以帮助我们评估电路的性能和稳定性。 总结起来，非正弦周期电流电路的分析不仅涉及基础的电路理论，还涵盖了傅里叶变换和信号处理等高级概念。理解和掌握这些知识点对于理解和解决实际工程问题具有重要意义。