XGBoost算法解析：构建与优化目标函数

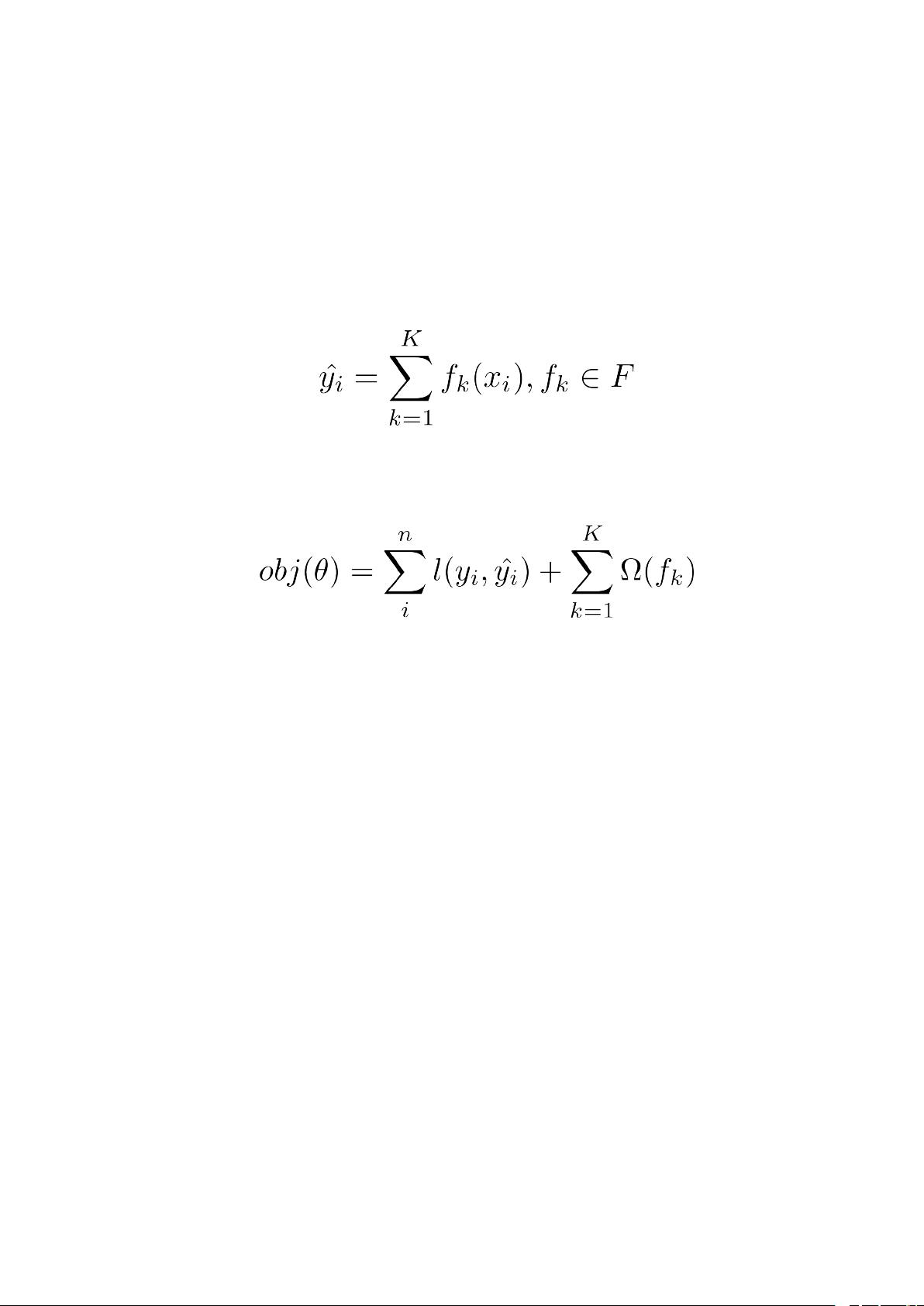
"非编程作业1，讨论XGBoost算法及其决策树原理" XGBoost算法是一种广泛应用的梯度提升决策树（Gradient Boosting Decision Tree, GBDT）框架，尤其在机器学习竞赛和实际项目中表现出色。它由陈天奇博士开发，其核心在于优化了GBDT的效率和泛化能力。 XGBoost模型基于 CART (Classification and Regression Trees) 决策树，通过连续添加树来逐步提高预测准确率。每一棵树的预测结果会累加到总预测分数上。模型的形式可以表示为所有CART树的预测分数之和： \( \hat{y} = \sum_{k=1}^{K} f_k(x) \) 这里，\( K \) 是树的数量，\( f_k \) 表示第 \( k \) 棵CART树。XGBoost的目标函数包含了损失函数和正则项，用于平衡模型的拟合程度和复杂度： \( L = \sum_{i=1}^{n} l(y_i, \hat{y}_i) + \sum_{k=1}^{K}\Omega(f_k) \) 其中，\( n \) 是样本数量，\( l \) 是损失函数，\( \Omega(f_k) \) 是正则化项，用于防止过拟合。正则项通常包括树的复杂度（如叶子节点数量）和叶子节点分数的平方和。 XGBoost采用加法训练方法，逐棵优化决策树。在第 \( t \) 步，它寻找一棵能最大程度减少目标函数的CART树 \( f_t \)，这棵树是基于前 \( t-1 \) 棵树的预测结果构建的： \( \arg\min_{f_t} L + \Omega(f_t) \) 当损失函数为均方误差（MSE）时，可以利用泰勒展开简化优化过程。在一阶和二阶导数的基础上，XGBoost仅需考虑二次可微的损失函数。 CART树的结构用函数 \( q(x) \) 表示，它将样本映射到特定的叶子节点，而 \( w_q(x) \) 是样本在该叶子节点上的预测值。正则化项可以写为： \( \Omega(f) = \lambda \sum_{j=1}^{T} w_j^2 + \gamma T \) 这里的 \( \lambda \) 和 \( \gamma \) 控制树的复杂度，较大的值会使树更加简单，因为更多的叶子节点会被较大的惩罚。 最终，XGBoost通过求解优化问题来确定每棵树的结构和叶子节点分数，以最小化目标函数。这种方法使得XGBoost能够高效地构建出既能有效拟合数据又避免过拟合的强预测模型。 总结来说，XGBoost算法是通过迭代构建CART决策树，逐步改进预测性能，同时通过正则化控制模型复杂度，确保良好的泛化能力。它在处理各种预测任务，特别是分类和回归问题时，展现出优秀的性能。