控制系统数学模型与线性化分析
需积分: 9 166 浏览量
更新于2024-08-01
收藏 284KB PPT 举报
"大学课程课件,包含自动控制系统中的经典控制部分,如线性系统的数学模型,传递函数,框图化简,以及如何建立控制系统模型等。"
在自动控制系统领域,数学模型是理解和分析系统行为的关键工具。本课件详细介绍了线性系统的数学模型,包括输入-输出传递函数描述、机理分析法、非线性环节的线性化处理等核心概念。首先,线性系统的输入-输出传递函数描述了系统对不同输入信号的响应方式,它是通过微分方程或传递函数来表示的。传递函数定义了一个系统在零初始条件下,输出对输入的拉普拉斯变换比,具有明确的物理意义,可以揭示系统的动态性能。
建立系统数学模型的机理分析法是从系统内部工作原理出发,基于物理定律(如基尔霍夫定律、牛顿定律等)建立描述系统运动的方程。在实际工程应用中,常常需要对非线性环节进行小范围线性化处理,以便于分析和设计。此外,框图和信号流程图是简化系统模型并进行计算的有效工具,梅逊公式则用于快速求解复杂框图的传递函数。
在建立控制系统数学模型的过程中,通常会遵循以下步骤:对系统进行线性化处理,建立近似的线性模型,然后分析系统的近似特性。这有助于我们理解系统的动态行为,并为控制器设计提供基础。模型建立方法主要包括机理分析法和实验辨识法,前者依赖于对系统工作原理的理解,后者则通过实验数据来确定模型参数。
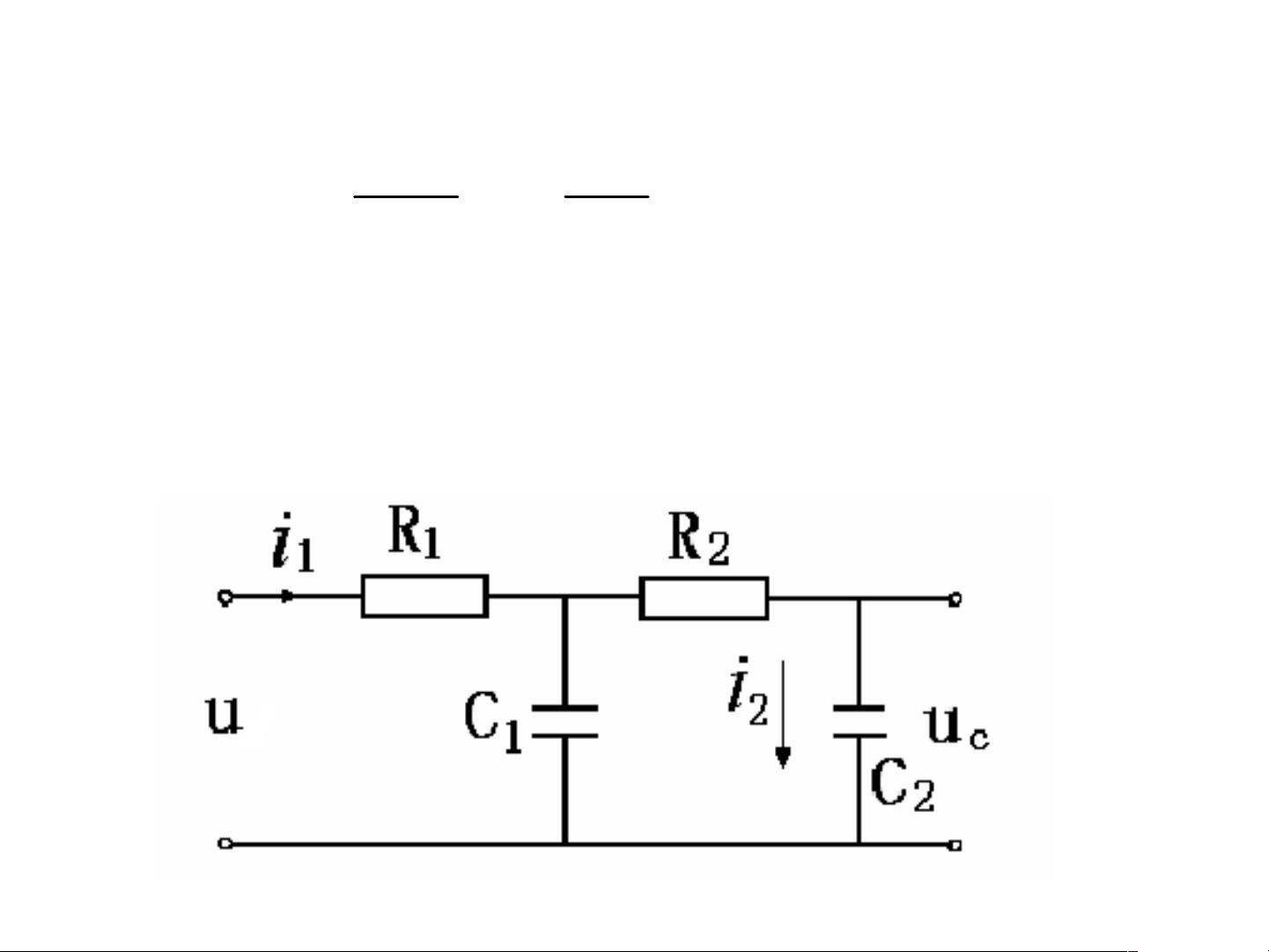
课件中举了两个实例来展示如何建立线性系统的输入-输出时间函数描述。第一个例子是弹簧阻尼系统,通过牛顿定律建立微分方程,求得输入力F与输出位移y的关系。第二个例子是RC滤波电路,通过分析电路工作原理,假设理想电阻和电容,建立输入电压u到输出电压uc的微分方程。这些实例深入浅出地展示了理论知识在实际问题中的应用。
这个大学课程课件提供了关于自动控制系统数学建模的全面介绍,对于学习控制系统理论和实践操作非常有帮助。通过对这些知识点的掌握,学生能够更好地理解和设计控制系统,解决实际工程问题。
相关推荐






feixuezj
- 粉丝: 0

最新资源
- 算符优先分析器:基于分析法的语法分析程序
- Google ADB工具包使用教程与文件解析
- 以太网POWERLINK资源:规范与PCAP报文解析
- 周立功讲授ARM技术精华课程
- MFC C++应用程序开发实战指南
- 掌握Superpowers-Redux:下一代JavaScript开发
- 简易性能计数器应用开发与本地化处理
- 一步到位:Maven Eclipse离线插件的直接使用教程
- WPF嵌入Win32控件实现摄像头功能的应用指南
- 掌握Excel VBA:从基础到进阶的应用技巧
- 深入解析莱昂氏UNIX源码与操作系统原理
- Informatica常用Transformation实例解析
- Windows平台高度自定义的ListView控件
- 掌握前端街机游戏开发:瓢虫迁徙挑战
- Lht蓝海豚PHP团购导航系统v4.0.3新功能介绍
- 掌握Bochs模拟器:新手入门与基础教程