C#递归全排列算法详解及去重实例

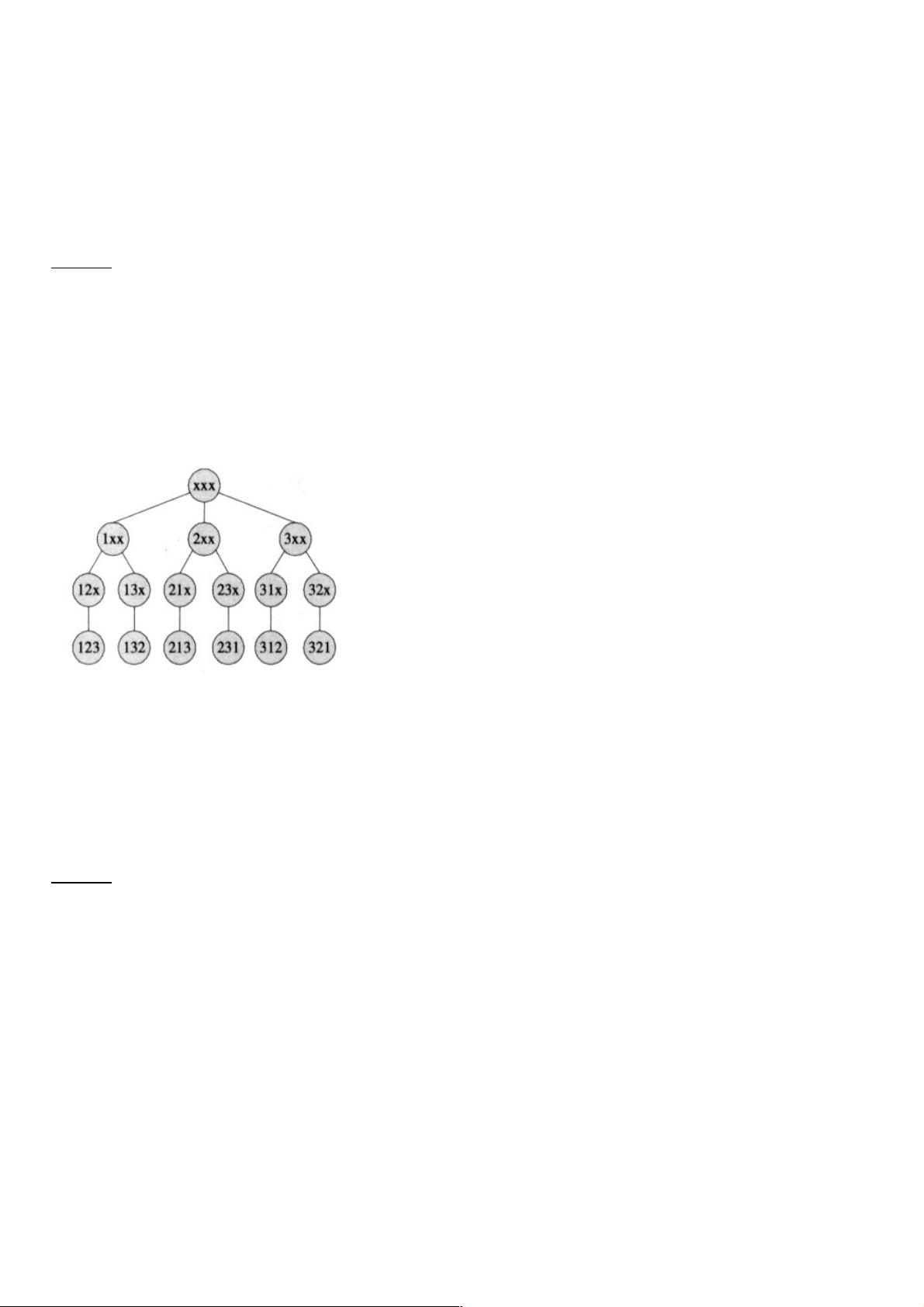
C#算法之全排列递归算法实例讲解深入解析 在C#编程中，全排列是一种常见的算法问题，尤其在需要生成所有可能的元素排列组合时非常有用。全排列指的是从n个不同元素中取出所有可能的m个元素序列，当n=m时，得到的是所有元素的唯一排列组合，也就是所谓的全排列。例如，对于集合{1,2,3}，全排列包括{123}, {132}, {213}, {231}, {321}, {312}这六个不同的排列。 全排列递归算法的关键在于理解其逻辑结构。算法的核心思想可以用以下步骤概括： 1. 递归定义：n个元素的全排列可以通过(n-1个元素的全排列)与剩余一个元素的所有可能位置组合来生成。这是一种分治策略，将大问题分解成小问题来解决。 2. 出口条件：当只剩下一个元素时，不再有排列的可能性，此时直接输出这个元素并结束递归。这是递归算法的终止条件。 3. 递归过程：对于每一个元素，首先将其设为第一个元素，然后递归处理剩下的(n-1)个元素，得到一个排列。接着，将当前元素移到下一个位置，再次递归处理，这样可以覆盖所有可能的排列组合。 4. 避免重复：在实际实现中，为了处理可能出现的重复元素，需要在每次交换元素后恢复原始状态，以防止重复计算相同的排列。例如，代码中通过`Swap`函数实现字符数组元素的临时交换，并在递归结束后通过`sum`变量记录不同排列的数量。 C#代码实例展示了如何利用递归方法实现全排列算法，包括`Swap`函数用于元素交换，以及`Perm`函数负责递归调用和排列生成。在`main`函数中，用户输入元素个数和元素本身，然后调用`Perm`函数生成所有排列，并统计总数。 总结来说，C#全排列递归算法是一种高效且简洁的方法，它利用了递归的思想，通过不断地将元素置于首位并调整其余元素的位置，直至所有可能的排列都被生成。这种算法在处理需要列举所有可能排列的问题时，如密码生成、数据排序等场景，具有重要意义。同时，理解如何处理重复元素是确保算法正确性的关键。