MATLAB实现：数字滤波器实战-巴特沃斯、高斯与低通/高通

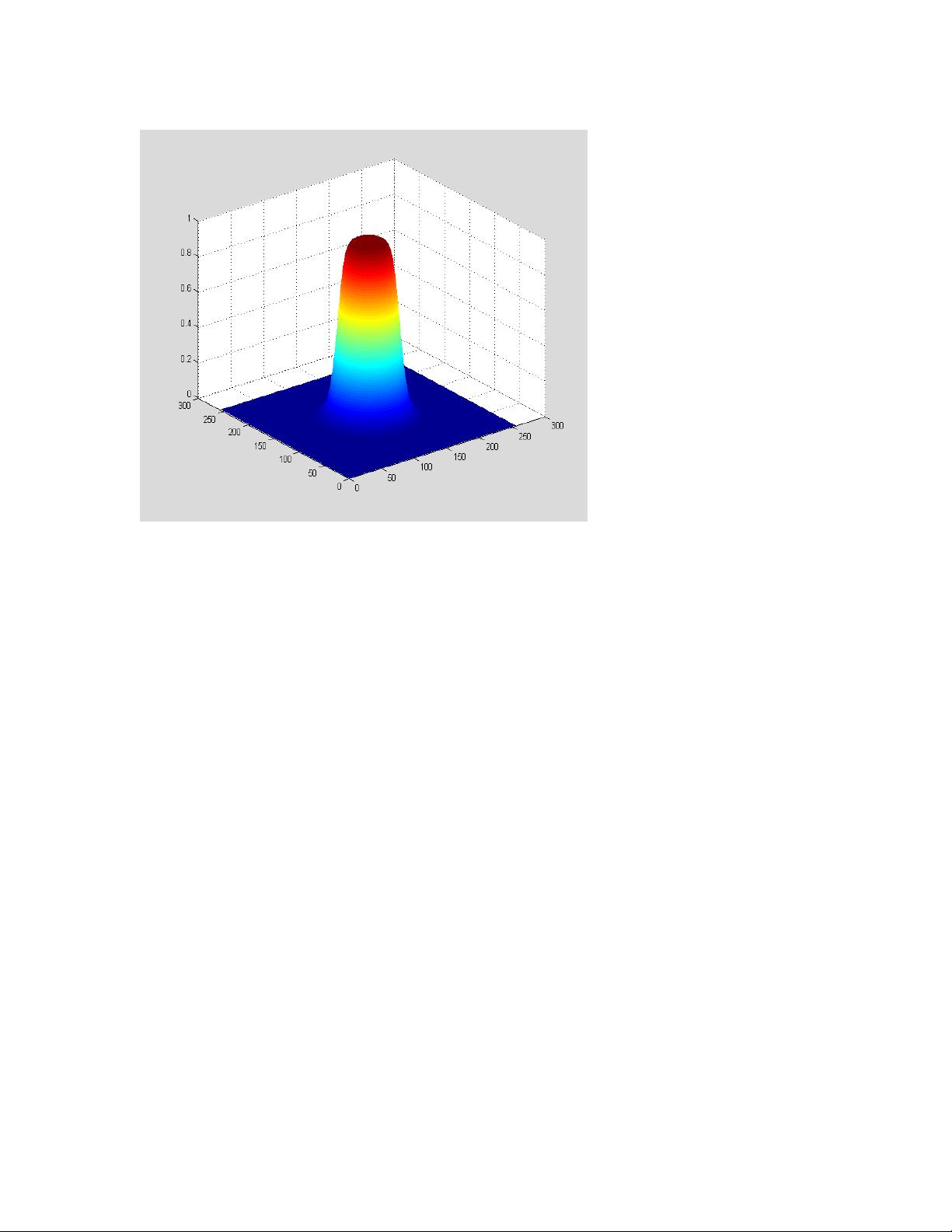
在MATLAB中，数字滤波器是一种用于处理数字信号的重要工具，特别是在图像处理领域，它们被广泛应用以增强、平滑或分离图像特征。本文将介绍几种常见的数字滤波器，包括理想低通滤波器、理想高通滤波器以及Butterworth低通滤波器。 1. **理想低通滤波器** 理想低通滤波器主要用于保留频率较低的部分，去除高频噪声。在MATLAB示例中，首先读取 Lena 图像，然后通过快速傅里叶变换（FFT）将其转换到频域。创建一个二维函数Hd，其中所有高于给定截止频率（这里是0.2）的频率分量被设为0。接着，对原图像进行卷积操作，并将结果反变换回时域，得到低通滤波后的图像。通过imshow显示原始图像和处理后的图像，可以看到滤波效果，以及通过surf函数展示滤波器的频率响应。 2. **理想高通滤波器** 理想高通滤波器则相反，它允许高频成分通过而抑制低频成分。在MATLAB中，同样的步骤应用于高通滤波，只是截止频率被设置在0.2以下，使得高频部分保持不变。处理后的图像同样通过imshow和surf展示。 3. **Butterworth低通滤波器** Butterworth滤波器是一种无极点零点的线性相位滤波器，特别适用于需要平坦频率响应的场合。在这个例子中，使用了Butterworth设计，通过计算频率域中的阶数n和截止频率D，构建了一个具有特定衰减特性的滤波器函数Hd。滤波过程包括频域卷积和反变换，最后得到的图像展示了低通特性。通过比较原始图像和处理后的图像，可以观察到Butterworth滤波器如何平滑图像并抑制高频噪声。 这些滤波器的实现方法不仅展示了MATLAB在数字信号处理中的强大功能，而且直观地展示了不同滤波类型在图像处理中的应用。通过调整截止频率和滤波器类型，用户可以根据具体需求优化图像质量，如去除噪声、细节增强或频域分析等。理解这些基本概念和MATLAB代码有助于提高图像处理技能，并在实际项目中灵活运用各种滤波技术。