多目标多播路由遗传算法MulRoGA：一种经典优化方法

需积分: 9 2 浏览量更新于2024-07-18 收藏 1.52MB PDF 举报

MulRoGA: A Multicast Routing Genetic Algorithm Approach 是一篇发表在2010年6月《应用智能》(Applied Intelligence)期刊上的研究论文，其作者是Aluizio F. R. Araújo和Cícero Garrozi。这篇经典的研究着重于多播路由问题，特别是采用遗传算法（Genetic Algorithm, GA）的多目标优化方法。在多播网络中，数据需要同时发送到多个接收节点，而有效的多播路由设计不仅要考虑带宽效率，还要关注延迟、可靠性和其他性能指标，这些构成了多目标优化问题。论文的核心内容是提出了一种名为MulRoGA的算法，它将遗传编程技术应用于解决多播路由问题。遗传算法在此情境下被用来模拟自然选择和进化过程，通过一代代迭代来搜索可能的最佳路由路径组合，以满足多个目标函数。这种算法的优势在于能够处理复杂的问题，并且能够找到全局最优解或近似最优解，尤其是在面对动态网络环境时，其适应性和灵活性至关重要。 MulRoGA的关键贡献在于其设计了适应性较强的多目标优化框架，能够在满足服务质量的同时兼顾网络资源的高效利用。通过种子讨论、统计分析以及作者的个人资料，我们可以看到该研究的影响和后续工作。Aluizio F. R. Araújo在联邦佩尼亚布洛科大学有丰富的研究成果，共发表了124篇论文，获得了992次引用，而Cícero Garrozi则来自巴西农村联邦大学，虽然论文数量较少，但也有10篇，得到32次引用。文章本身在2008年10月29日首次在线发布，Springer Science+Business Media出版，DOI为10.1007/s10489-008-0148-5。全文探讨了如何将遗传算法与多播路由结合，提供了一种创新的方法来处理现实网络中的复杂多目标问题。阅读这篇文章不仅可以深入理解遗传算法在多播路由中的应用，还能学习如何在实际网络环境中平衡多个性能指标，这对于网络管理员和研究人员来说是一份极具价值的参考资料。

332 A.F.R. Araújo, C. Garrozi

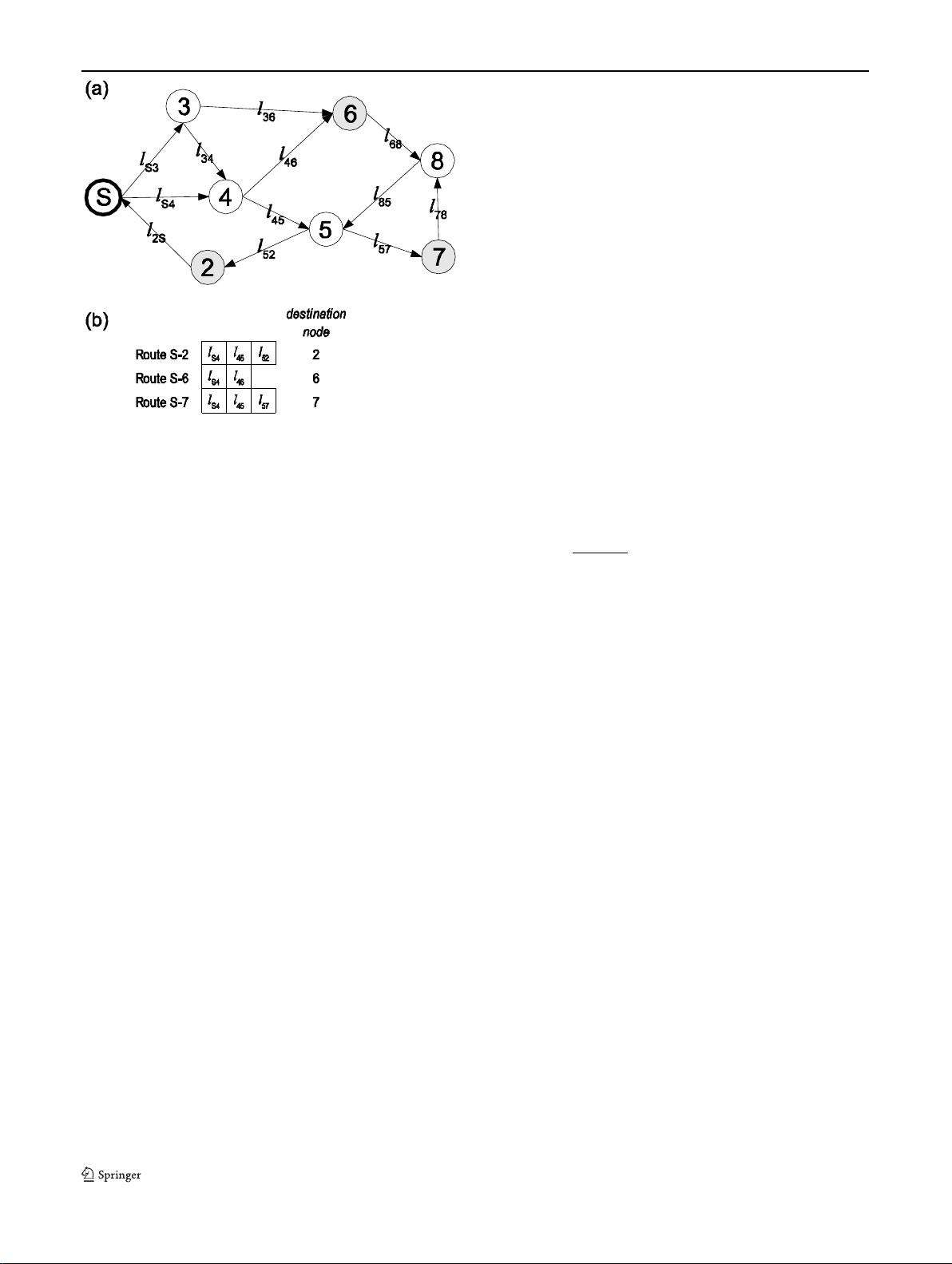
Fig. 1 A representation example: (a) A network with source node S

and twelve unidirectional links. The gray nodes form the multicast

group; (b) An individual with three chromosomes (routes) and a vari-

able number of genes (links)

links. A viable route (a feasible chromosome) must have

a sequence of links from the initial node to a destination

node which are topologically connected, i.e., each pair of

links must share a common node, so that, at the end of each

feasible chromosome, the destination node is reached. Fig-

ure 1 shows an instance of an individual with three chromo-

somes. From this point onwards, a route is deﬁned as a set of

paths from the source-node (S) to a destination node (D

whereas a multicast route is deﬁned as the routes from S

(starting node) to the multicast group (D

,i =1,...,M).

The randomly generated initial population takes into ac-

count the existence of actual connections between two con-

secutive network nodes as a local constraint. An empty chro-

mosome is ﬁlled as follows: choose randomly a link, from

the source node to any other node in the network, and place it

at the ﬁrst locus; ﬁll the subsequent loci following the same

procedure. A link cannot be selected more than once, hence,

whenever there are no viable links to be chosen at any step,

the chromosome is not completely ﬁlled and the destination

node is not reached. Thereafter, variation operators will act

to improve incomplete paths.

2.2 Multiobjective optimization problems

A general multiobjective optimization problem (MOP) com-

bines two or more objectives to determine the overall goal.

Such objectives often affect each other in complex and non-

linear ways [27]. Formally, a MOP can be stated as:

Find the vector X

∗

=[x

∗

,...,x

∗

]

that optimizes the

function:

G(X) =(g

(X), g

(X),...,g

(X)) (1)

satisfying the constraints of m inequality

(X) ≥0 i =1, 2,...,m (2)

and the constraints of (z −m) equality

(X) =0 j =m +1,m+2,...,z (3)

where X is the vector of decision variables [28], and g

(X)

with v = 1,...,u are objective functions often mutually

conﬂicting in nature. In some approaches, the constraints

are also treated as objective functions. There are also ap-

proaches in which a number of objectives are treated as con-

straints in order to reduce the dimensionality of the objective

space [29].

The current problem takes into consideration three ob-

jectives, hence the aim is to maximize the function G(X) =

(g

(X), g

(X)) in which g

(X), g

(X), and g

(X)

consider the number of common paths, the total length of the

route, and a reward for viable routes (or absence of violated

constraints), respectively. Hence, the objective function is

given as follows

G(X) =1 −

(X)

+ω

(X) (4)

where ω

,ω

are the weights of real value functions.

Equation (4) is subject to constraints which limit the maxi-

mum and the minimum number of links of a route and es-

tablish the connections of each route, as follows:



q,r∈H

≤L

max

(5)



q,r∈H

≥L

min

(6)



q,r,s∈H

·l

=1 with q =s (7)

where q,r,s are indices of the network nodes in each chro-

mosome (route) H

,i =1,...,M, and l

is a potential link

(gene) from node j to node k within route H , i.e., l

is an

element of the network connection matrix which has values

of 0 for each link absent or of 1 for each existing link. For

this case, L

max

=L;L

min

=1. Equations (5)–(6) restrict the

minimum and maximum number of paths and (7) checks if

each path is actually connected within the network, taking

the value 1 if it is fully connected and value 0 otherwise.

2.3 Fitness function

In this paper we propose the following ﬁtness function. The

objective function (4) is transformed into a ﬁtness function

剩余16页未读，继续阅读

solibear

粉丝: 7
资源: 1

多目标多播路由遗传算法MulRoGA：一种经典优化方法

Cisco Press： Interdomain Multicast Solutions Guide.chm

A multicast routing algorithm based on searching in directed graph

Delay-constrained least-energy-consumption multicast routing based on heuristic genetic algorithm in unreliable wireless networks

Cisco Networkers 2000：PIM multicast routing详解与部署策略

Interdomain Multicast Routing

IP multicast routing

A new green multicast grooming protection algorithm in WDM optical networks

Cisco Multicast Routing And Switching MCGRAW-HILL 1999

Distributed QoS-aware source-specific multicast routing protocol (2005年)

dou.rar_QoS matlab_matlab Qos_multicast routing_蚁群 qos_蚁群路由Mat

最新资源