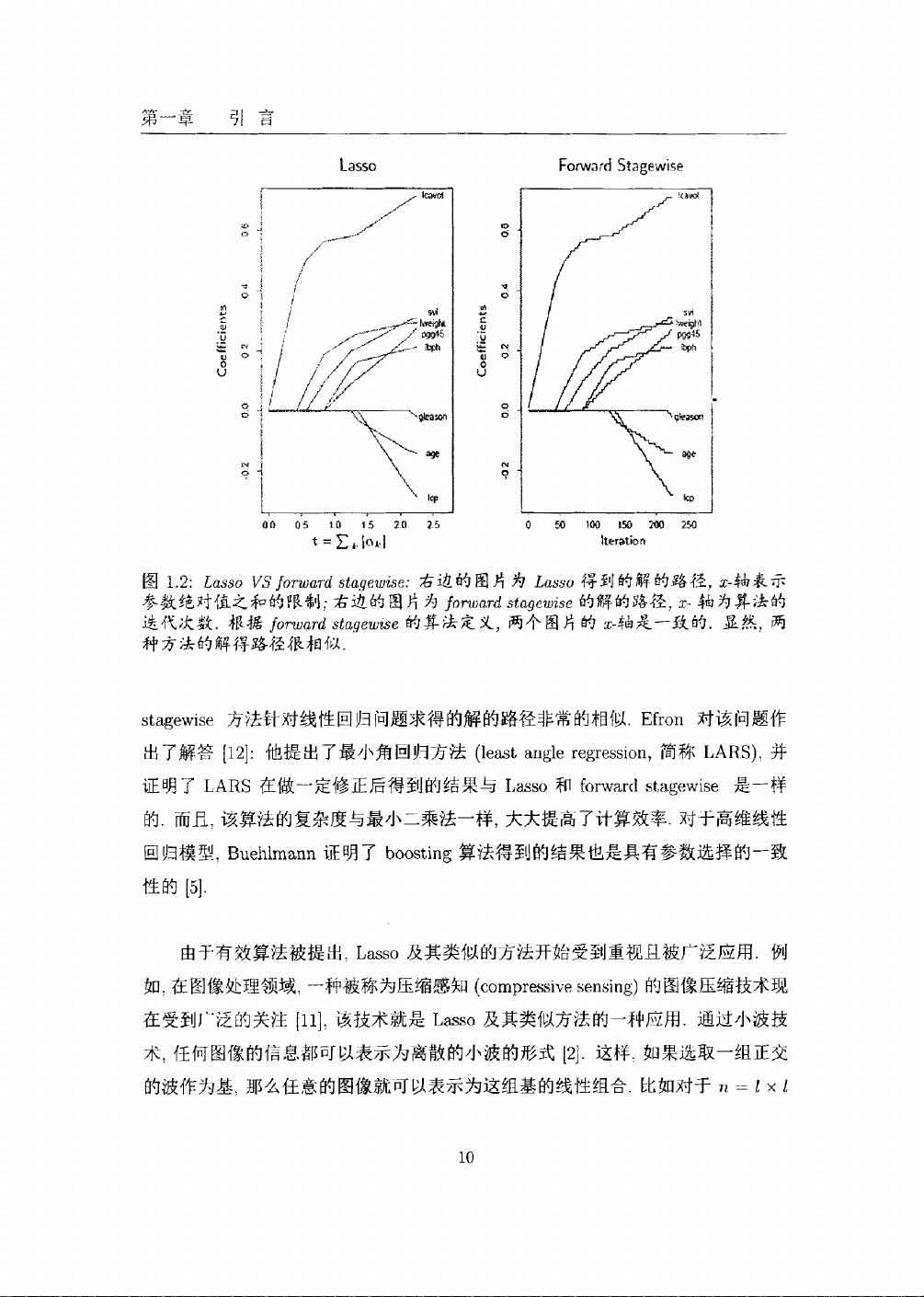
高维线性回归的Adaptive Lp正则化：渐近性质探讨

“数据回归-对于使用Adaptive Lp正则化的线性回归问题在高维情况下渐近性质的讨论” 这篇论文聚焦于高维线性回归模型中的Adaptive Lp正则化方法，特别是当0 < P < 1时的情况。在统计学和机器学习中，线性回归是一种常见的建模技术，用于研究因变量和一个或多个自变量之间的关系。然而，在高维数据集（特征数量远大于样本数量）中，传统的线性回归模型可能会遇到挑战，如过拟合问题。为了克服这些问题，正则化技术被引入，其中Lp正则化（尤其是L1和L2正则化）是两种常用的方法。 Adaptive Lp正则化是一种改进的正则化策略，它通过调整每个参数的惩罚权重来适应不同的特征重要性。与Lasso（L1正则化）相比，Adaptive Lp正则化可以更好地处理非稀疏解决方案，并且在选择变量（变量选择）和估计参数（参数估计）方面可能更有效。在高维设置下，这种正则化方法能够帮助识别重要的变量，同时忽略不相关的特征，从而提高模型的预测性能。 论文特别关注当样本量和变量数量都趋向于无穷大时，Adaptive Lp正则化估计器的渐近性质。传统的“Oracle属性”是评估正则化估计器性能的一个关键指标，它意味着即使在不知道哪些变量真正相关的假设下，估计器也能达到与知道这些信息的理想情况相媲美的表现。在固定变量数量的情况下，已经证明了Adaptive Lp正则化具有Oracle属性。然而，这篇论文扩展了这一结果，提出了在变量数量无限增加时保持Oracle属性的具体条件。 论文还介绍了一种通过二次规划算法实现Adaptive Lp正则化的算法，并通过模拟实验与Lasso、Adaptive Lasso、Lp正则化以及普通的最小二乘法（OLS）进行了比较。这些比较旨在展示Adaptive Lp正则化在不同情况下的优势和适用性。 关键词包括Oracle属性、Adaptive Lp正则化、变量选择、零一致性和损失函数，这些都是理解和评估正则化技术核心概念的关键术语。通过深入探讨这些主题，论文为高维线性回归模型的理论和实践提供了有价值的贡献。