《Essential Calculus》早期超越函数电子书-理论与应用
需积分: 34 51 浏览量
更新于2024-07-18
收藏 22.71MB PDF 举报
" Essential Calculus: Early Transcendental Functions 是一本由Ron Larson、Robert Hostetler和Bruce H. Edwards合著的大学数学教材，主要涵盖了微积分的基础知识及其在不同领域的应用。这本书分为13个章节，深入浅出地介绍了极限、微分、积分、级数以及多元函数等多个核心概念。"
此书详细讲解了以下几个关键知识点：
1. **极限与它们的性质**（Chapter 1）：这一章主要介绍极限的概念，包括极限的定义、极限的求法、无穷小量和无穷大、极限运算法则以及极限的存在性。这些基础知识为微积分提供了理论基础。
2. **微分**（Chapter 2）：微分是微积分的核心部分，讨论了导数的定义、计算方法、导数的几何意义以及物理解释，如速度和加速度。此外，还包括高阶导数、隐函数的导数和参数方程的导数。
3. **微分的应用**（Chapter 3）：这里探讨了微分在实际问题中的应用，如利用导数找函数的极值、解决优化问题以及曲线的切线和凹凸性分析。
4. **积分**（Chapter 4）：介绍了不定积分和定积分的基本概念，积分的几何和物理意义，如面积、体积和工作量的计算。还包括基本积分表和部分分式分解等求积分的方法。
5. **积分的应用**（Chapter 5）：讨论积分在物理、工程等领域中的应用，如定积分在求解物理问题中的作用，如质心、弧长、功和流量等。
6. **积分技巧，L'Hôpital's规则和不恰当积分**（Chapter 6）：进一步探讨了洛必达法则用于处理0/0或∞/∞型未定义形式的极限，以及处理无穷大积分和无穷区间上的积分。
7. **无穷级数**（Chapter 7）：涵盖几何级数、调和级数、泰勒级数和幂级数，以及级数的收敛性测试，如比较测试、比值测试和积分测试。
8. **圆锥曲线、参数方程和极坐标**（Chapter 8）：介绍如何用参数方程和极坐标表示和理解二维空间的曲线，包括椭圆、双曲线和抛物线。
9. **向量与空间几何**（Chapter 9）：涉及三维空间中的向量运算，包括向量的数量积、向量积和混合积，以及向量在解析几何中的应用。
10. **向量值函数**（Chapter 10）：研究多变量函数，特别是向量函数的微分学，包括方向导数、梯度矢量和曲率。
11. **多个变量的函数**（Chapter 11）：介绍多元函数的极限、连续性、偏导数、全微分和多元函数的最大值和最小值。
12. **多重积分**（Chapter 12）：包括二重积分和三重积分的计算，以及积分在物理和几何中的应用，如求体积和质量。
13. **向量分析**（Chapter 13）：讨论矢量场、格林定理、斯托克斯定理和高斯定理，将微积分扩展到矢量函数和流形上。
这本教材广泛使用现实生活中的数据和各种软件技术输出，使学习者能够将抽象概念与实际问题联系起来，有助于提高对微积分的理解和应用能力。
Features
Section Openers
Every section begins with an outline of the key
concepts covered in the section. This serves as a
class planning resource for the instructor and
a study and review guide for the student.
Explorations
For selected topics, Explorations offer the opportunity
to discover calculus concepts before they are formally
introduced in the text, thus enhancing student under-
standing. This optional feature can be omitted at the
discretion of the instructor with no loss of continuity
in the coverage of the material.
Historical Notes
Integrated throughout the text, Historical Notes help
students grasp the basic mathematical foundations
of calculus.
xv
Essential Calculus offers a number of proven
pedagogical features developed by the Larson team
to promote student mastery of Calculus. In order to
streamline this version for faster paced courses, we
have moved some content to online resources, leaving
the essential course content presented in a variety of
ways to appeal to different learning styles, instructional
approaches, and course configurations.
EXPLORATION
Integrating a Radical Function
Up to this point in the text, you have
not evaluated the following integral.
From geometry, you should be able to
find the exact value of this integral—
what is it? Using numerical integra-
tion with Simpson’s Rule or the
Trapezoidal Rule, you can’t be sure
of the accuracy of the approximation.
Why?
Try finding the exact value using the
substitution
and
Does your answer agree with the
value you obtained using geometry?
dx cos
d
.
x sin
1
1
1 x
2
dx
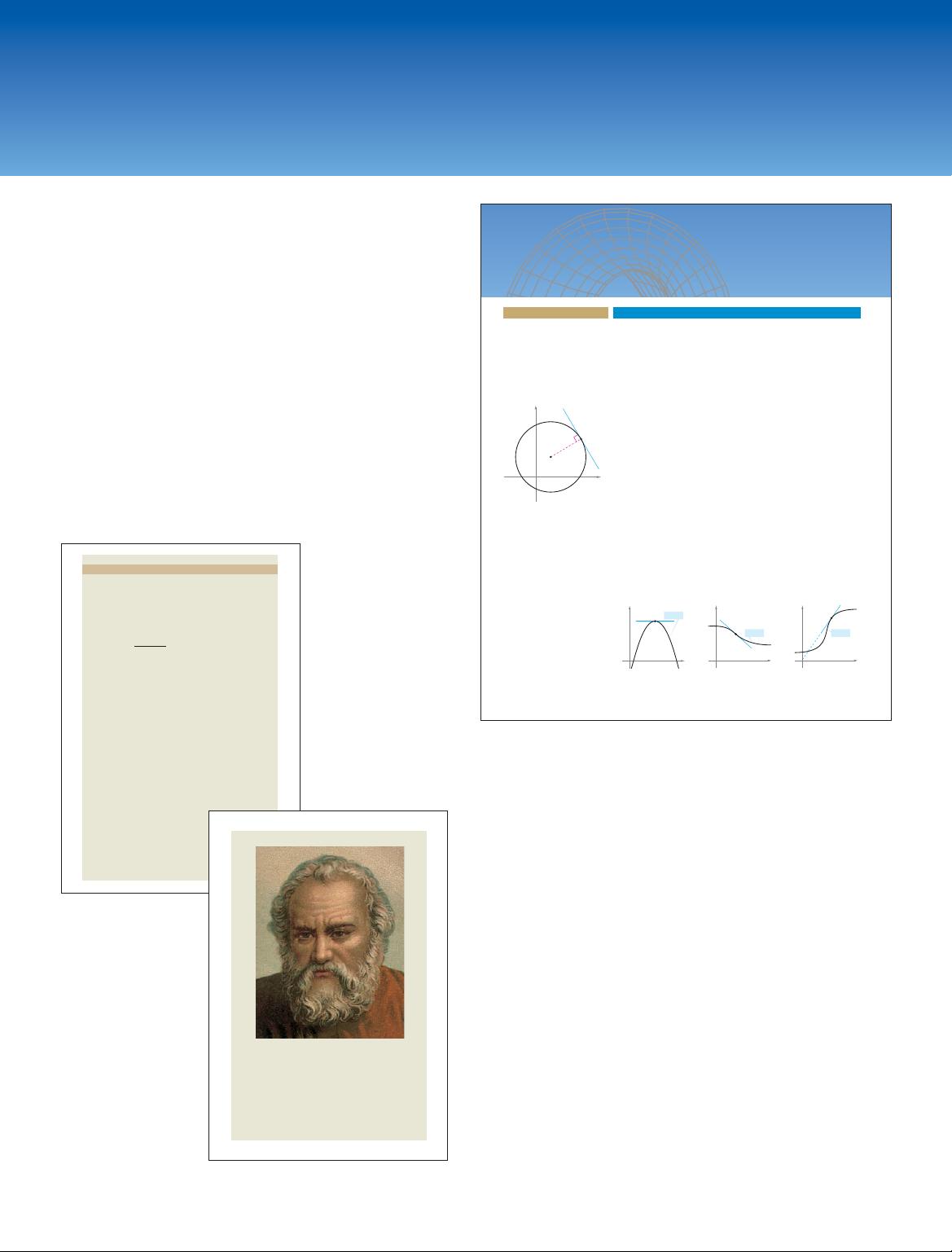
ARCHIMEDES (287–212 B.C.)
Archimedes used the method of exhaustion to
derive formulas for the areas of ellipses,
parabolic segments, and sectors of a spiral.
He is considered to have been the greatest
applied mathematician of antiquity.
Mary Evans Picture Library
80
Section 2.1 The Derivative and the Tangent Line Problem
• Find the slope of the tangent line to a curve at a point.
• Use the limit definition to find the derivative of a function.
• Understand the relationship between differentiability and continuity.
The Tangent Line Problem
Calculus grew out of four major problems that European mathematicians were work-
ing on during the seventeenth century.
1. The tangent line problem (this section)
2. The velocity and acceleration problem (Sections 2.2 and 2.3)
3. The minimum and maximum problem (Section 3.1)
4. The area problem (Section 4.2)
Each problem involves the notion of a limit, and calculus can be introduced with any
of the four problems.
Although partial solutions to the tangent line problem were given by Pierre de
Fermat (1601–1665), René Descartes (1596–1650), Christian Huygens (1629–1695),
and Isaac Barrow (1630 –1677), credit for the first general solution is usually given to
Isaac Newton (1642–1727) and Gottfried Leibniz (1646–1716). Newton’s work on
this problem stemmed from his interest in optics and light refraction.
What does it mean to say that a line is tangent to a curve at a point? For a circle,
the tangent line at a point is the line that is perpendicular to the radial line at point
as shown in Figure 2.1.
For a general curve, however, the problem is more difficult. For example, how
would you define the tangent lines shown in Figure 2.2? You might say that a line is
tangent to a curve at a point if it touches, but does not cross, the curve at point
This definition would work for the first curve shown in Figure 2.2, but not for the
second. Or you might say that a line is tangent to a curve if the line touches or
intersects the curve at exactly one point. This definition would work for a circle but
not for more general curves, as the third curve in Figure 2.2 shows.
P.P
P,
P
x
P
y
Tangent line to a circle
Figure 2.1
x
P
y
= f(x)
y
x
P
y
= f(x)
y
x
P
y
= f(x)
y
Tangent line to a curve at a point
Figure 2.2
F
OR FURTHER INFORMATION For
more information on the crediting of
mathematical discoveries to the first
“discoverer,” see the article
“Mathematical Firsts—Who Done It?”
by Richard H. Williams and Roy D.
Mazzagatti in Mathematics Teacher.
To view this article, go to the website
www.matharticles.com.
2
Differentiation
剩余1012页未读，继续阅读
点击了解资源详情
点击了解资源详情
点击了解资源详情
2009-07-19 上传
2019-09-14 上传
2010-03-31 上传
2021-09-09 上传
2021-09-13 上传
wxa_9
- 粉丝: 0
- 资源: 5
我的内容管理
展开
最新资源
- Mathematics for Computer Graphics
- Tomcat 安装配置手册
- web课件第九章 ASP.NET的XML编程
- Java Struts教程
- 基于PLC的步进电机控制系统及其在火车轴温检测系统中的应用.pdf
- Eclipse中文教程
- 基于TCPIP的局域网多用户通信
- oracle动态过程执行
- WEB SERVICE
- 嵌入式Linux驱动开发实例分析
- linux c 编程.pdf
- 1_必读_高质量C++编程指南(林锐博士).pdf
- c语言指针经验总结.pdf
- kr.ac.jbnu.ssel.misrac:OpenMRC
- ogov-importer:阿根廷国会法案进口商
- 大数据导论PPT和期末复习笔记
