随机过程概要：泊松过程与马氏过程解析

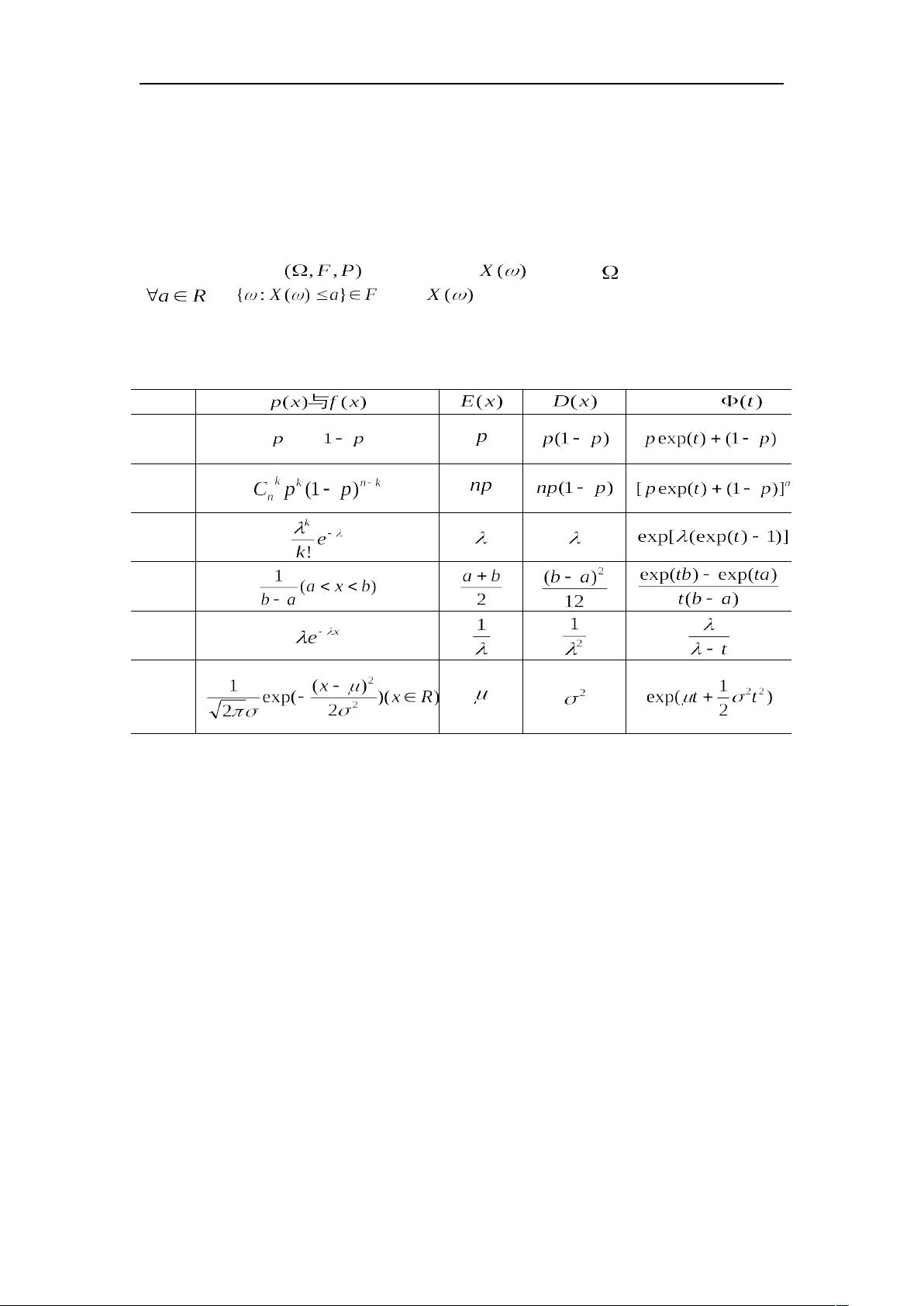
"这篇资料是对清华大学出版的随机过程教材的总结，主要涵盖了随机过程的基本概念，特别是泊松过程和马氏过程。它旨在帮助读者理解和掌握这些重要的概率论与统计学概念。" 随机过程是概率论中的一个重要分支，用于描述在时间上随机变化的系统状态。在第一章预备知识中，介绍了随机变量的基础知识，包括不同类型的随机变量分布，如两点分布、二项分布、泊松分布、均匀分布、指数分布和正态分布，以及它们的矩母函数。矩母函数是研究随机变量性质的重要工具，可以帮助计算期望值和方差。 全期望公式[pic]阐述了期望值的线性性质，即期望值的运算可以扩展到更复杂的随机变量组合上，这是概率论中一个非常基础且实用的定理。 第二章深入讨论了泊松过程，这是一个极其重要的随机过程模型。泊松过程具有四个关键特性：零初值性、独立增量性、增量平稳性和普通性。这些特性使得泊松过程在处理离散事件发生的时间序列问题时特别有用。例如，泊松过程常被用来模拟在特定时间区间内随机事件（如顾客到达、电话呼叫或机器故障）的发生次数。相邻事件的时间间隔服从指数分布，而剩余寿命和年龄的概念则进一步揭示了事件发生的连续性和随机性。 马氏过程在随机过程中的地位同样重要，但文件中没有具体展开。马氏过程是一种状态转移具有马尔科夫性质的随机过程，即当前状态只依赖于其前一个状态，而不依赖于过去的历史状态。这种过程广泛应用于物理、化学、生物学、经济学等领域，用来建模具有记忆性的动态系统。 通过深入理解随机过程、泊松过程和马氏过程，可以更好地分析和预测现实世界中的各种随机现象，如交通流量、股票市场波动、生物种群动态等。对于学习和研究这些领域的人员来说，这份总结是宝贵的参考资料。