动力学第五章习题解析：滑轮组、摆的运动微分方程

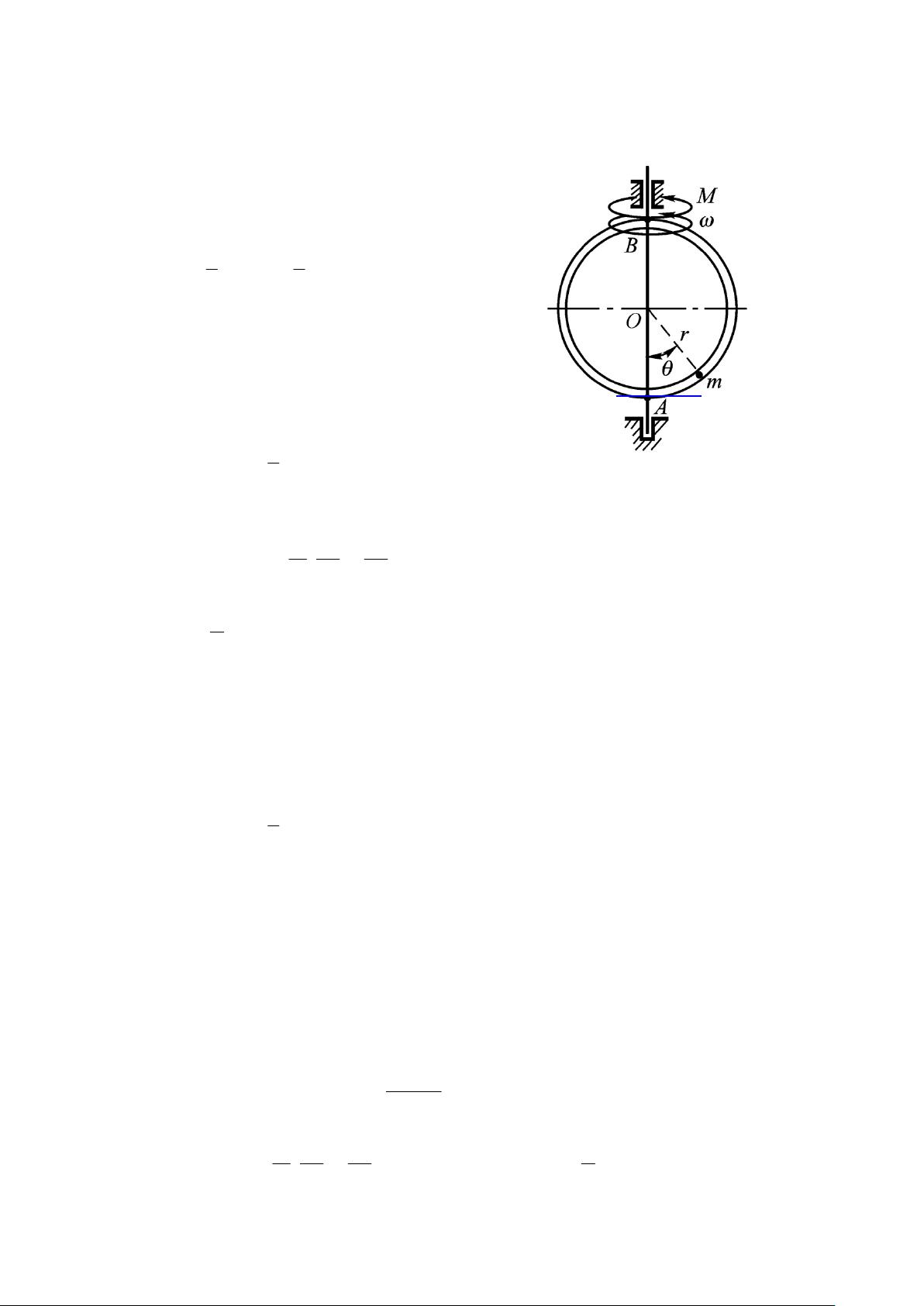
"动力学第五章部分习题解答包括滑轮组问题、摆的运动微分方程和旋轮线导轨中的质点运动规律" 在动力学第五章中，我们探讨了几个关键概念和问题的解答。首先，针对滑轮组的问题，我们需要考虑的是力的平衡和加速度的计算。在5-2题中，有两个质量分别为10kg和8kg的重物通过滑轮相连。由于忽略滑轮质量，系统中只有重力是主动力。通过对系统进行分析，我们可以利用牛顿第二定律来解决加速度和绳子拉力的问题。通过设定虚位移并应用动力学普遍方程，可以得出重物的加速度和绳子拉力的表达式。 接着，5-4题涉及到一个摆动问题，质量为m的质点在一半径为R的固定圆柱体上构成一个摆。这里，我们使用拉格朗日力学来解决运动微分方程。拉格朗日函数结合动能和势能，然后代入拉格朗日方程，可以得到描述摆运动的方程。这个方程反映了质点在摆动过程中的动态行为。 最后，5-6题涉及一个在旋轮线导轨上运动的质点。旋轮线是一种特殊的曲线，其运动规律需要通过分析质点的动能和势能来确定。同样运用拉格朗日力学，找到系统的广义坐标，构建拉格朗日函数，再代入拉格朗日方程，从而获得质点的运动微分方程。解这个方程，我们可以得到质点沿旋轮线运动的具体轨迹。 这些习题解答涵盖了经典力学中的基本概念，如力的平衡、加速度的计算、虚位移的应用以及拉格朗日力学在解决复杂动力学问题中的有效性。通过这些练习，学生可以深化对动力学的理解，提高分析和解决问题的能力。