非线性方程求解:区间二分法与迭代技巧
需积分: 28 56 浏览量
更新于2024-09-03
收藏 557KB PDF 举报
在科学计算领域,非线性方程的数值求解是一项关键任务,因为实际问题中的物理现象和工程问题往往涉及到复杂的非线性关系。本资源深入探讨了非线性方程求根问题的解决方案,主要包括区间二分法和迭代法。
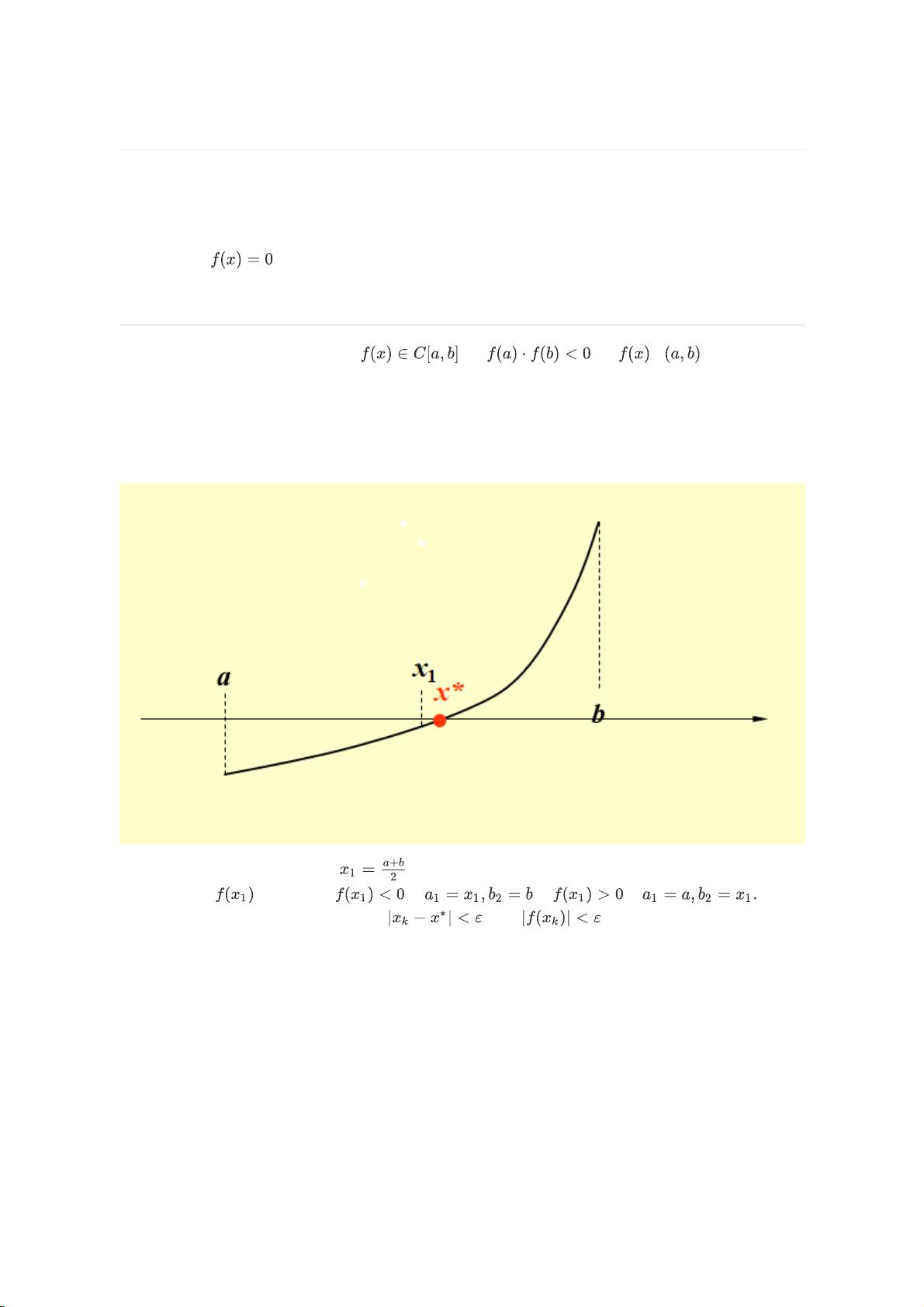
首先,区间二分法是一种基于定理的搜索策略,它假设如果函数f在闭区间[a, b]上连续,且f(a) * f(b) < 0,那么在该区间内必然存在至少一个零点。其操作步骤包括选择区间中点x_c,判断f(x_c)的符号,然后根据符号决定下一步区间,直至达到预设的精度标准或达到最大迭代次数。这种方法的优点是简单直观,但缺点是可能无法处理有重根的情况,并且对初始区间的选择较为敏感。
为了克服这些问题,迭代法引入了不动点的概念,将非线性方程的根求解转化为寻找函数g(x)的不动点。其中,Newton迭代法是最基本的形式,通过设置初始值x_0,不断逼近解的序列{x_n},直到满足收敛条件。全局收敛定理确保了当满足某些条件时,无论初始值如何,迭代序列总会收敛到唯一解,同时给出了误差估计。然而,初始值的选择对于迭代法的性能至关重要,通常需要结合全局和局部收敛性来优化。
对于具体迭代格式如固定步长法,其收敛速度可以通过收敛阶来衡量。收敛阶越高,迭代收敛得越快,但实际计算中,确定收敛阶和渐近误差常数通常是理论上的挑战。为提高迭代效率,可以对基本迭代函数g(x)进行加速,例如采用迭代-加速技术,通过构造更复杂的迭代公式来改善收敛速度。
总结来说,非线性方程的数值求解是一个涉及理论与实践相结合的过程,涵盖了区间搜索方法、不动点理论以及迭代法的迭代策略选择和优化。理解并熟练运用这些方法和技术对于解决实际问题中的非线性方程至关重要。
551 浏览量
116 浏览量
200 浏览量
2019-09-10 上传
107 浏览量
2023-03-06 上传
112 浏览量
2021-06-27 上传