傅立叶变换与傅立叶级数解析

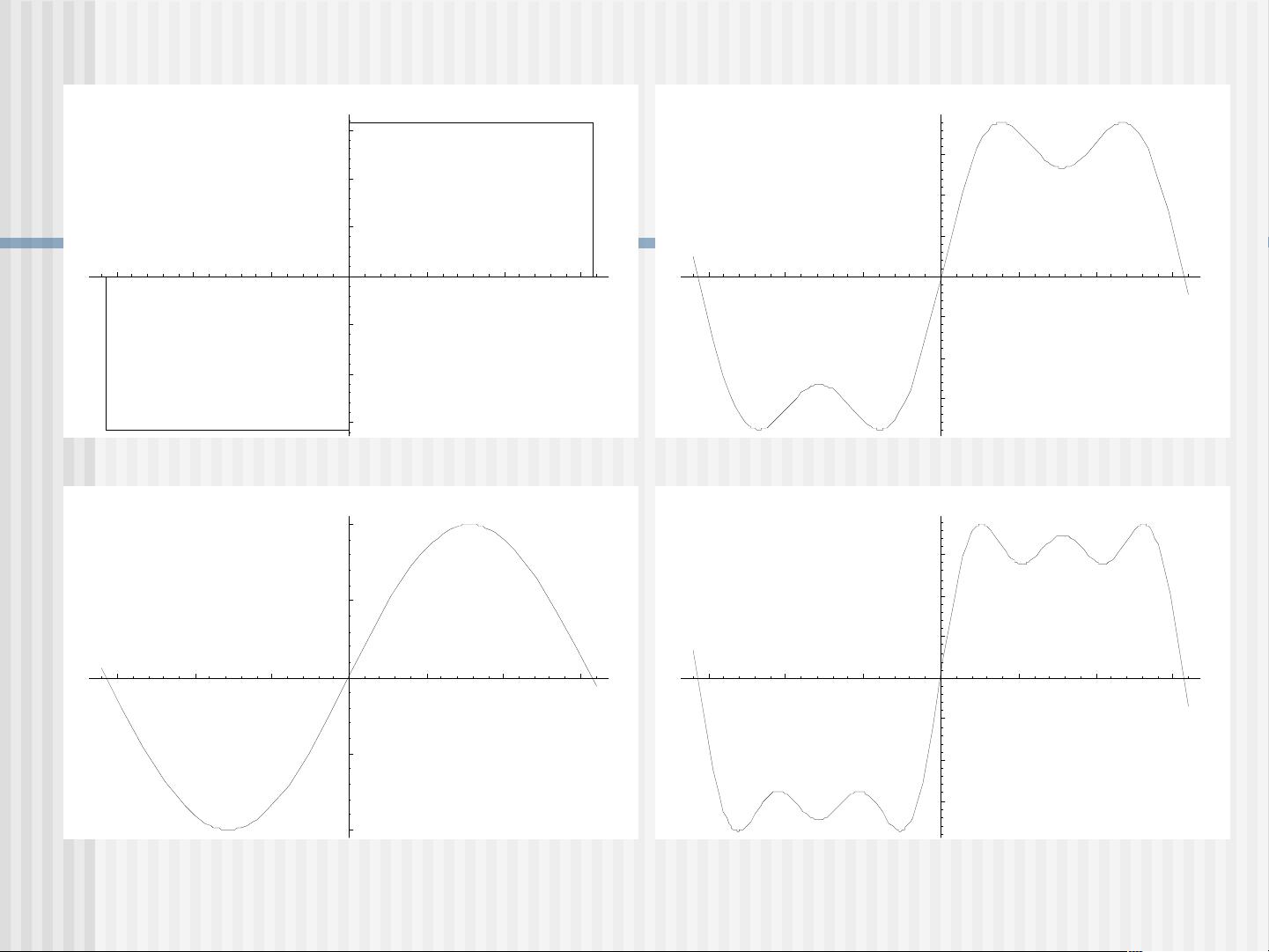
"傅立叶变换与傅立叶级数是数学物理方法中的核心概念，它们在处理周期性信号和复杂函数表示上有着重要应用。傅立叶级数是将周期为2π的函数表示为无限个正弦和余弦函数的线性组合，其基本函数包括1、cos(nx)和sin(nx)，具有正交性。傅立叶展开定理指出任何这样的函数都可以展开为三角级数，其系数可以通过函数与基本函数的积分子积求得。狄利克雷收敛定理给出了级数收敛的条件和收敛结果，对于连续点，级数收敛于函数值；对于间断点，收敛于左右极限的平均值。傅立叶变换是傅立叶级数的广义形式，适用于非周期函数。对称函数、奇函数和偶函数的傅立叶展开有特定形式。傅立叶变换和傅立叶级数的意义在于理论上的简化表达以及实际应用中的信号分析和近似表示，如对称方波的傅立叶展开。" 傅立叶变换和傅立叶级数是分析周期性信号和复杂函数的重要工具。傅立叶级数的基本思想是将一个周期函数f(x)拆解为一系列简单周期函数（正弦和余弦）的和，这样复杂的函数就可以被简化为易于处理的形式。这一过程称为傅立叶展开，其展开式包含了不同频率的正弦和余弦项，系数通过与原函数的积分相关联的公式计算得出。 傅立叶变换则是傅立叶级数的连续极限形式，它将函数从时域（或空间域）转换到频域，揭示了函数在不同频率成分上的分布情况。对于周期函数，傅立叶变换可以看作是傅立叶级数的频率域表示。傅立叶变换在信号处理、图像分析、通信工程等领域有广泛的应用。 狄利克雷收敛定理是傅立叶级数收敛性的判据，它规定了函数在什么条件下其傅立叶级数会收敛。如果函数在一个周期内连续或者只有有限个第一类间断点，并且极值点有限，那么傅立叶级数就会收敛。在连续点上，级数收敛于函数值；在间断点处，级数收敛于该点的左右极限的平均值。 傅立叶级数的具体应用包括但不限于对各种周期函数的分析，如对称函数、奇函数和偶函数。例如，一个对称的方波可以通过傅立叶级数表示为不同频率的正弦波之和，这种方式不仅可以帮助理解信号的本质，还可以用于信号的重构和滤波。 傅立叶变换和傅立叶级数是理解和处理周期性现象的强大工具，它们在理论研究和实际应用中都有着不可替代的地位。通过这些理论，我们可以将复杂的周期函数转化为简单的三角函数组合，进而更好地理解和操纵这些函数。