Linux LVM教程：添加新硬盘扩展存储并管理逻辑卷

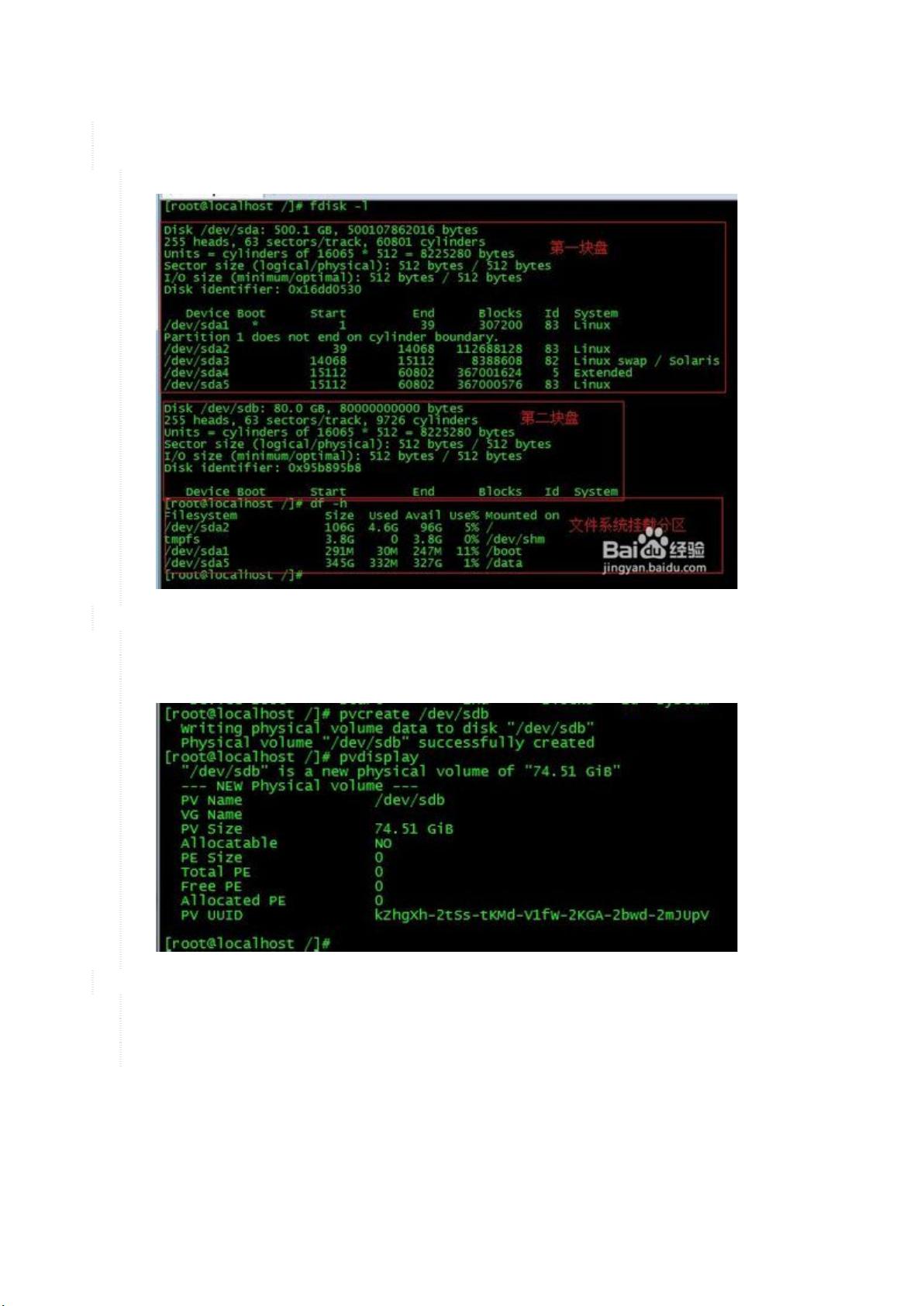
在Linux环境下，当需要向已有的系统中添加新硬盘并扩展文件系统时，LVM (Logical Volume Manager) 是一个重要的工具。以下是一个详细的步骤指南： 1. **查看现有硬件和分区情况**： 在Linux中，通常使用`lsblk`命令来查看硬盘及其分区信息，如`/dev/sda`和`/dev/sdb`分别代表第一和第二个SCSI硬盘。对于分区，可以通过`fdisk -l`或`ls /dev/sd*`查看。 2. **初始化新硬盘为物理卷（PV）**： 使用`pvcreate`命令初始化新硬盘，如`pvcreate /dev/sdb`，这会创建一个物理卷设备。然后通过`pvdisplay`命令检查物理卷的信息，确保初始化成功。 3. **创建逻辑卷组（VG）**： 创建一个新的逻辑卷组，比如`VolGroup00`，并将其添加物理卷到该组，`vgcreate VolGroup00 /dev/sdb`。再次运行`vgdisplay`验证新的卷组及其成员。 4. **创建逻辑卷（LV）**： 为扩展文件系统，创建一个名为`LogVol00`的逻辑卷，指定大小为700M，例如`lvcreate -L 700M -n LogVol00 VolGroup00`。`lvdisplay`用于检查逻辑卷状态。 5. **格式化逻辑卷**： 使用`mkfs.ext4`命令格式化新创建的逻辑卷，如`mkfs.ext4 /dev/mapper/VolGroup00-LogVol00`。这时，`/dev/mapper/VolGroup00-LogVol00`指向逻辑卷的文件系统。 6. **挂载逻辑卷**： 将逻辑卷挂载到某个目录，如`mount /dev/mapper/VolGroup00-LogVol00 data2`。这是为了在不干扰现有数据的情况下使用新增空间。 7. **扩展文件系统之前的安全步骤**： 在进行扩展操作前，务必确保`/data2`目录下的数据已备份，防止意外丢失。 8. **添加新硬盘并扩展逻辑卷**： 对于新添加的硬盘分区（如`/dev/sda5`），重复上述物理卷、卷组和逻辑卷的操作。首先初始化`pvcreate /dev/sda5`，然后`vgextend VolGroup00 /dev/sda5`，增加卷组容量。 9. **调整逻辑卷大小**： 使用`lvextend -L +500M /dev/mapper/VolGroup00-LogVol00`来扩大`LogVol00`的大小，这里增加了500M。 10. **重新挂载逻辑卷到文件系统**： 最后，将扩展后的逻辑卷挂载回原来的文件系统位置，如`mount /dev/mapper/VolGroup00-LogVol00 data`。 通过以上步骤，你可以有效地在Linux系统中添加新硬盘，并通过LVM技术扩展已有的文件系统，以适应不断增长的数据需求。务必小心操作，尤其是在扩展过程中备份重要数据，以避免潜在的数据损失。