A*算法解八数码：Nilsson序列得分解析

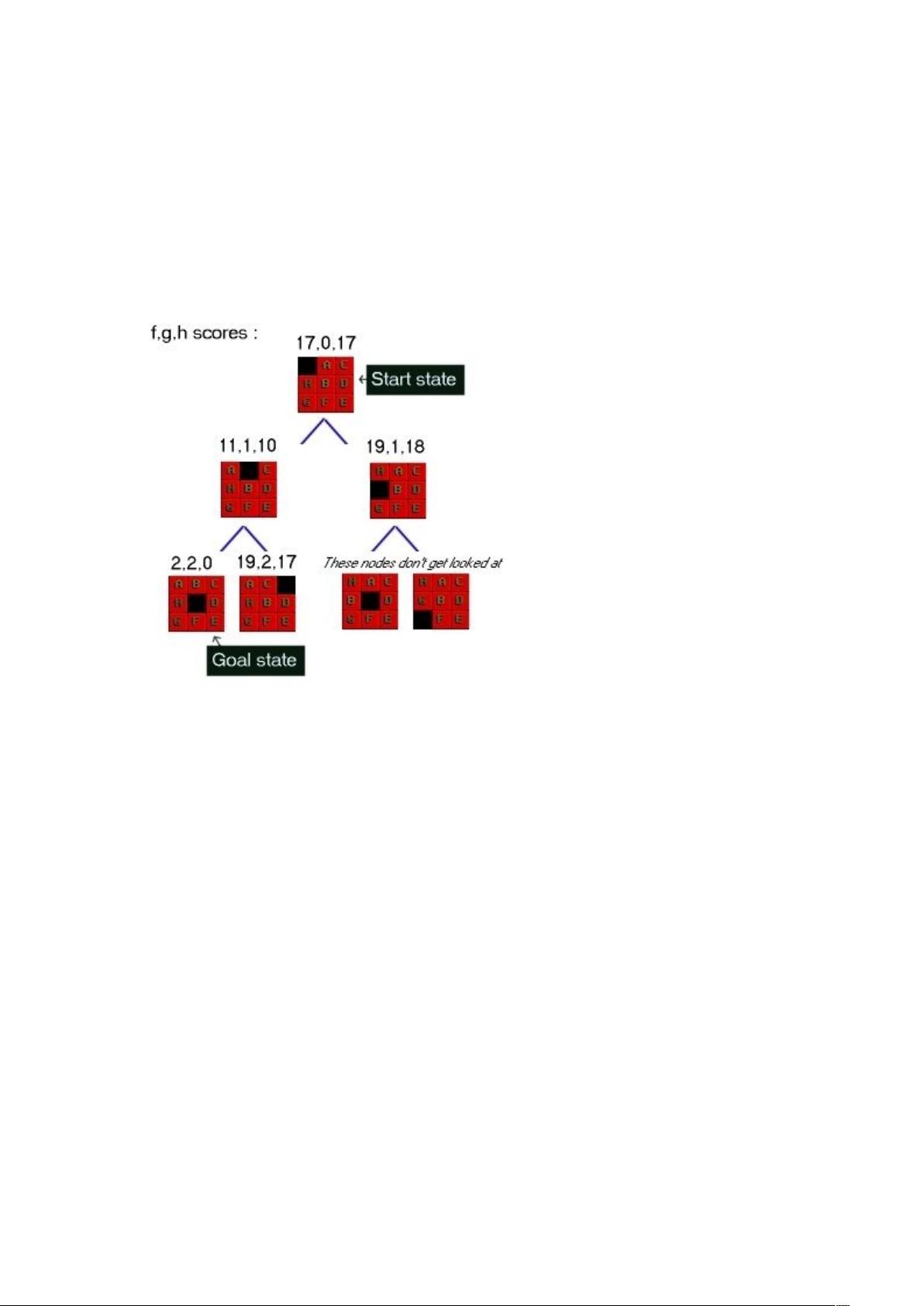
"A*算法在解决八数码难题中的应用，特别是使用Nilsson序列得分作为估价函数的方法。 Nilsson序列得分考虑了每个棋子的位置、空位以及相邻棋子的正确顺序，通过曼哈顿距离和特定规则计算得出。" 在解决经典的八数码难题时，A*算法是一种常用的搜索策略，它结合了最佳优先搜索和启发式搜索的优点。A*算法的核心在于计算节点的总成本，由已知成本`g(n)`和预计成本`h(n)`组成，即`f(n) = g(n) + h(n)`。`g(n)`是从初始状态到当前节点的实际步数，而`h(n)`是对从当前节点到达目标状态所需步数的估算。 在这个问题中，Nilsson序列得分被用来估计`h(n)`。这个估价函数考虑了两个关键因素：每个棋子离其目标位置的距离以及棋盘上棋子的相对顺序。 1. **曼哈顿距离** (`P(n)`)： 曼哈顿距离是指棋子从当前位置到目标位置所需的水平和垂直移动步数之和。在八数码问题中，如果棋子`X`从位置`(i, j)`移动到目标位置`(x, y)`，则其曼哈顿距离为`|i - x| + |j - y|`。计算所有棋子的曼哈顿距离之和，即为`P(n)`。 2. **Nilsson序列得分** (`S(n)`)： 这个部分的得分基于棋子之间的相对位置。中心位置的棋子（在目标状态下应为空）如果非空，得分1分。对于其他位置的棋子，如果顺时针方向的下一个棋子不是目标状态中相应位置的棋子，那么得2分。所有其他位置的棋子不计分。将这些得分乘以3，然后加上`P(n)`的值，就得到了`h(n)`的最终值，即`h(n) = P(n) + 3S(n)`。 举例来说，考虑以下初始状态`I`和目标状态`T`： 初始状态I： ``` *AC HBD GFE ``` 目标状态T： ``` ABC H*D GFE ``` 计算曼哈顿距离`P(n)`，我们发现只有A和B需要移动，因此`P(n) = 1（A的移动步数）+ 1（B的移动步数）= 2`。 接下来，计算`S(n)`。在初始状态`I`中，B在中心，所以得分1。检查其他棋子，我们发现没有棋子满足错误的后继结点条件，因此`S(n) = 1`。将`S(n)`乘以3，得到`3S(n) = 3`。 最后，`h(n)`为`h(n) = P(n) + 3S(n) = 2 + 3 = 5`。 通过这样的估价函数，A*算法能更有效地找到解决八数码问题的最小步数路径。这种策略减少了搜索空间，提高了算法效率，使得复杂的问题变得更容易解决。